Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-24T13:53:58.714Z Has data issue: false hasContentIssue false
  • English
  • Français

Symmetry breaking of azimuthal thermo-acoustic modes in annular cavities: a theoretical study

Published online by Cambridge University Press:  11 November 2014

M. Bauerheim ,
P. Salas ,
F. Nicoud  and
T. Poinsot
M. Bauerheim*
Affiliation:
CERFACS, CFD team, 42 Av Coriolis, 31057 Toulouse, France Société Nationale d’Etude et de Construction de Moteurs d’Aviation, 77550 Reau, France
P. Salas
Affiliation:
INRIA Bordeaux – Sud Ouest, HiePACS Project, Joint INRIA-CERFACS lab. on High Performance Computing, 33405 Talence, France
F. Nicoud
Affiliation:
Université Montpellier 2. I3M UMR CNRS 5149, France
T. Poinsot
Affiliation:
IMF Toulouse, INP de Toulouse and CNRS, 31400 Toulouse, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Many physical problems containing rotating symmetry exhibit azimuthal waves, from electromagnetic waves in nanophotonic crystals to seismic waves in giant stars. When this symmetry is broken, clockwise (CW) and counter-clockwise (CCW) waves are split into two distinct modes which can become unstable. 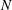This paper focuses on a theoretical study of symmetry breaking in annular cavities containing a number $N$ of flames prone to azimuthal thermo-acoustic instabilities. A general dispersion relation for non-perfectly-axisymmetric cavities is obtained and analytically solved to provide an explicit expression for the frequencies and growth rates of all azimuthal modes of the configuration. This analytical study unveils two parameters affecting the stability of the mode: (i) a coupling strength corresponding to the cumulative effects of the 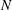$N$ flames and (ii) a splitting strength due to the symmetry breaking when the flames are different. This theory has been validated using a 3D Helmholtz solver and good agreement is found. When only two types of flames are introduced into the annular cavity, the splitting strength is found to depend on two parameters: the difference between the two burner types and the pattern used to distribute the flames along the azimuthal direction. To first order, this theory suggests that the most stable configuration is obtained for a perfectly axisymmetric configuration. Therefore, breaking the symmetry by mixing different flames cannot improve the stability of an annular combustor independently of the flame distribution pattern.

JFM classification

Acoustics: Acoustics Instability: Instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 760 , 10 December 2014 , pp. 431 - 465
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barman, A., Barman, S., Kimura, T., Fukuma, Y. & Otani, Y. 2010 Gyration mode splitting in magnetostatically coupled magnetic vortices in an array. J. Phys. D: Appl. Phys. 43, 422001.CrossRefGoogle Scholar
Bauerheim, M., Cazalens, M. & Poinsot, T.2014a A theoretical study of mean azimuthal flow and asymmetry effects on thermo-acoustic modes in annular combustors. Proceedings of the 35th Combustion Institute (in press); doi:10.1016/j.proci.2014.05.053.CrossRefGoogle Scholar
Bauerheim, M., Nicoud, F. & Poinsot, T. 2014b Theoretical analysis of the mass balance equation through a flame at zero and non-zero Mach numbers. Combust. Flame (in press); doi:10.1016/j.combustflame.2014.06.017.Google Scholar
Bauerheim, M., Parmentier, J. F., Salas, P., Nicoud, F. & Poinsot, T. 2014c An analytical model for azimuthal thermoacoustic modes in an annular chamber fed by an annular plenum. Combust. Flame 161, 1374–1389.Google Scholar
Berenbrink, P. & Hoffmann, S.2001 Suppression of dynamic combustion instabilities by passive and active means, GT2001-42.Google Scholar
Blimbaum, J., Zanchetta, M., Akin, T., Acharya, V., O’Connor, J., Noble, D. R. & Lieuwen, T. 2012 Transverse to longitudinal acoustic coupling processes in annular combustion chambers. Intl J. Spray Combust. Dyn. 4 (4), 275–298.CrossRefGoogle Scholar
Borisnika, S. V. 2006 Symmetry, degeneracy and optical confinement of modes in coupled microdisk resonators and photonic crystal cavities. IEEE J. Sel. Top. Quant. Electron. 12 (6), 1175–1182.Google Scholar
Bourgouin, J.-F., Durox, D., Moeck, J. P., Schuller, T. & Candel, S.2013 Self-sustained instabilities in an annular combustor coupled by azimuthal and longitudinal acoustic modes, GT2013-95010.Google Scholar
Busse, F. H. 1984 Oscillations of a rotating liquid drop. J. Fluid Mech. 142, 1–8.CrossRefGoogle Scholar
Creighton, J. A. 1982 Splitting of degenerate vibrational modes due to symmetry perturbations in tetrahedral m4 and octahedral m6 clusters. Inorg. Chem. 21 (1), 1–4.Google Scholar
Crocco, L. 1951 Aspects of combustion instability in liquid propellant rocket motors. Part I. J. Am. Rocket Soc. 21, 163–178.Google Scholar
Culick, F. E. C. & Kuentzmann, P.2006 Unsteady motions in combustion chambers for propulsion systems. NATO Research and Technology Organization.Google Scholar
Cummings, D. L. & Blackburn, D. A. 1991 Oscillations of magnetically levitated aspherical droplets. J. Fluid Mech. 224, 395–416.Google Scholar
Davey, A. & Salwen, H. 1994 On the stability in an elliptic pipe which is nearly circular. J. Fluid Mech. 281, 357–369.Google Scholar
Davies, P. O. A. L. 1988 Practical flow duct acoustics. J. Sound Vib. 124 (1), 91–115.CrossRefGoogle Scholar
Dowling, A. P. 1995 The calculation of thermoacoustic oscillations. J. Sound Vib. 180 (4), 557–581.Google Scholar
Evesque, S. & Polifke, W.2002 Low-order acoustic modelling for annular combustors: validation and inclusion of modal coupling, GT2002-30064.CrossRefGoogle Scholar
Evesque, S., Polifke, W. & Pankiewitz, C.2003 Spinning and azimuthally standing acoustic modes in annular combustors, AIAA Paper 2003-3182.Google Scholar
Feng, Z. C. & Sethna, P. R. 1989 Symmetry-breaking bifurcation in resonant surface waves. J. Fluid Mech. 199, 495–518.CrossRefGoogle Scholar
Gelbert, G., Moeck, J. P., Paschereit, C. O. & King, R. 2012 Feedback control of unstable thermoacoustic modes in an annular Rijke tube. Control Engng Practice 20, 770–782.CrossRefGoogle Scholar
Guckenheimer, J. & Mahalov, A. 1992 Instability induced by symmetry reduction. Phys. Rev. Lett. 68, 2257.Google Scholar
Guslienko, K. Y., Slavin, A. N., Tiberkevich, V. & Kim, S. K. 2008 Dynamic origin of azimuthal modes splitting in vortex-state magnetic dots. Phys. Rev. Lett. 24, 247203.Google Scholar
Hoffmann, F., Woltersdorf, G., Perzlmaier, K., Slavin, A. N., Tiberkevich, V. S., Bischof, A., Weiss, D. & Back, C. H. 2007 Mode degeneracy due to vortex core removal in magnetic disks. Phys. Rev. B 76, 014416.Google Scholar
Kammerer, M., Weigand, M., Curcic, M., Sproll, M., Vansteenkiste, A., Waeyenberge, B. V., Stoll, H., Woltersdorf, G., Back, C. H. & Schuetz, G. 2011 Magnetic vortex core reversal by excitation of spin waves. Nat. Commun. 2, 279; doi:10.1038/ncomms1277.Google Scholar
Kippenberg, T. J. 2010 Microresonators: particle sizing by mode splitting. Nat. Photon. 4, 9–10.Google Scholar
Kopitz, J., Huber, A., Sattelmayer, T. & Polifke, W.2005 Thermoacoustic stability analysis of an annular combustion chamber with acoustic low order modeling and validation against experiment, GT2005-68797. Reno, NV, USA.Google Scholar
Kosovichev, A. G. 1999 Inversion methods in helioseismology and solar tomography. J. Comput. Appl. Maths 109, 1–39.Google Scholar
Krebs, W., Flohr, P., Prade, B. & Hoffmann, S. 2002 Thermoacoustic stability chart for high intense gas turbine combustion systems. Combust. Sci. Technol. 174, 99–128.Google Scholar
Krueger, U., Hueren, J., Hoffmann, S., Krebs, W., Flohr, P. & Bohn, D. 2000 Prediction and measurement of thermoacoustic improvements in gas turbines with annular combustion systems. Trans. ASME J. Engng Gas Turbines Power 123 (3), 557–566.Google Scholar
Kumar, A. & Krousgrill, C. M. 2012 Mode-splitting and quasi-degeneracies in circular plate vibration problems: the example of free vibrations of the stator of a travelling wave ultrasonic motor. J. Sound Vib. 331 (26), 5788–5802.Google Scholar
Lavely, E. M.1983 Theoretical investigations in helioseismology. PhD thesis, Columbia University.Google Scholar
Lieuwen, T. & Yang, V. 2005 Combustion Instabilities in Gas Turbine Engines. Operational Experience, Fundamental Mechanisms and Modeling, Progress in Astronautics and Aeronautics, vol. 210. AIAA.Google Scholar
Lin, J. & Parker, R. G. 2000a Mesh stiffness variation instabilities in two-stage gear systems. J. Vib. Acoust. 124, 68–76.Google Scholar
Lin, J. & Parker, R. G. 2000b Structured vibration characteristics of planetary gears with unequally spaced planets. J. Sound Vib. 235 (5), 921–928.Google Scholar
Marble, F. E. & Candel, S. 1977 Acoustic disturbances from gas nonuniformities convected through a nozzle. J. Sound Vib. 55, 225–243.CrossRefGoogle Scholar
Mazzei, A., Gotzinger, S., Menezes, L. de. S., Zumofen, G., Benson, O. & Sandoghdar, V. 2007 Controlled coupling of counterpropagating whispering-gallery modes by a single Rayleigh scatterer: a classical problem in a quantum optical light. Phys. Rev. Lett. 99, 173603.Google Scholar
Moeck, J. P., Paul, M. & Paschereit, C.2010 Thermoacoustic instabilities in an annular flat Rijke tube, GT2010-23577.Google Scholar
Nicoud, F., Benoit, L., Sensiau, C. & Poinsot, T. 2007 Acoustic modes in combustors with complex impedances and multidimensional active flames. AIAA J. 45, 426–441.Google Scholar
Noiray, N., Bothien, M. & Schuermans, B. 2011 Analytical and numerical analysis of staging concepts in annular gas turbines. Combust. Theor. Model. 15 (5), 585–606.Google Scholar
Noiray, N., Durox, D., Schuller, T. & Candel, S. 2008 A unified framework for nonlinear combustion instability analysis based on the flame describing function. J. Fluid Mech. 615, 139–167.Google Scholar
Noiray, N. & Schuermans, B. 2013 On the dynamic nature of azimuthal thermoacoustic modes in annular gas turbine combustion chambers. Proc. R. Soc. Lond. A 469 (2151).Google Scholar
O’Connor, J. & Lieuwen, T.2012a Influence of transverse acoustic modal structure on the forced response of a swirling nozzle flow, GT2012-70053.Google Scholar
O’Connor, J. & Lieuwen, T. 2012b Recirculation zone dynamics of a transversely excited swirl flow and flame. Phys. Fluids 24, 075107.Google Scholar
O’Connor, J. & Lieuwen, T. 2012c Further characterization of the disturbance field in a transversely excited swirl-stabilized flame. Trans. ASME J. Engng Gas Turbines Power 134 (1), 011501.CrossRefGoogle Scholar
O’Connor, J. & Lieuwen, T. 2014 Transverse combustion instabilities: acoustic, fluid mechanics and flame processes. Prog. Energy Combust. Sci. (in press).Google Scholar
Oefelein, J. C. & Yang, V. 1993 Comprehensive review of liquid-propellant combustion instabilities in F-1 engines. J. Propul. Power 9 (5), 657–677.Google Scholar
Palies, P.2010 Dynamique et instabilités de combustion de flammes swirlées. PhD thesis, Ecole Centrale Paris.Google Scholar
Pang, L., Tetz, K. A. & Fainman, Y. 2007 Observation of the splitting of degenerate surface plasmon polariton modes in a two-dimensional metallic nanohole array. Appl. Phys. Lett. 90 (11), 111103.Google Scholar
Pankiewitz, C. & Sattelmayer, T. 2003 Time domain simulation of combustion instabilities in annular combustors. Trans. ASME J. Engng Gas Turbines Power 125 (3), 677–685.CrossRefGoogle Scholar
Parmentier, J. F., Salas, P., Wolf, P., Staffelbach, G., Nicoud, F. & Poinsot, T. 2012 A simple analytical model to study and control azimuthal instabilities in annular combustion chamber. Combust. Flame 159, 2374–2387.Google Scholar
Perrin, R. & Charnley, T. 1973 Group theory and the bell. J. Sound Vib. 31 (4), 411–418.Google Scholar
Pierce, A. D. 1981 Acoustics: an Introduction to its Physical Principles and Applications. McGraw-Hill.Google Scholar
Poinsot, T. & Veynante, D. 2011 Theoretical and Numerical Combustion, 3rd edn. www.cerfacs.fr/elearning.Google Scholar
Polifke, W., Poncet, A., Paschereit, C. O. & Doebbeling, K. 2001 Reconstruction of acoustic transfer matrices by instationary computational fluid dynamics. J. Sound Vib. 245 (3), 483–510.Google Scholar
Schuermans, B., Bellucci, V. & Paschereit, C.2003 Thermoacoustic modeling and control of multiburner combustion systems, GT2003-38688.Google Scholar
Schuermans, B., Paschereit, C. & Monkewitz, P.2006 Non-linear combustion instabilities in annular gas-turbine combustors, AIAA paper 2006-0549.Google Scholar
Schuller, T., Durox, D., Palies, P. & Candel, S. 2012 Acoustic decoupling of longitudinal modes in generic combustion systems. Combust. Flame 159, 1921–1931.Google Scholar
Selle, L., Benoit, L., Poinsot, T., Nicoud, F. & Krebs, W. 2006 Joint use of compressible large-eddy simulation and Helmholtz solvers for the analysis of rotating modes in an industrial swirled burner. Combust. Flame 145 (1–2), 194–205.CrossRefGoogle Scholar
Sensiau, C., Nicoud, F. & Poinsot, T. 2009 A tool to study azimuthal and spinning modes in annular combustors. Intl J. Aeroacoust. 8 (1), 57–68.Google Scholar
Silva, C. F., Nicoud, F., Schuller, T., Durox, D. & Candel, S. 2013 Combining a Helmholtz solver with the flame describing function to assess combustion instability in a premixed swirled combustor. Combust. Flame 160, 1743–1754.Google Scholar
Silva, F., Guillemain, Ph., Kergomard, J., Mallaroni, B. & Norris, A. N. 2009 Approximation formulae for the acoustic radiation impedance of a cylindrical pipe. J. Sound Vib. 322, 255–263.Google Scholar
Simonelli, F. & Gollub, J. P. 1989 Surface wave mode interactions: effects of symmetry and degeneracy. J. Fluid Mech. 199, 471–494.Google Scholar
Staffelbach, G., Gicquel, L. Y. M., Boudier, G. & Poinsot, T. 2009 Large eddy simulation of self-excited azimuthal modes in annular combustors. Proc. Combust. Inst. 32, 2909–2916.Google Scholar
Stow, S. R. & Dowling, A. P.2001 Thermoacoustic oscillations in an annular combustor, GT2001-0037, New Orleans, Louisiana.Google Scholar
Stow, S. R. & Dowling, A. P.2003 Modelling of circumferential modal coupling due to Helmholtz resonators, GT2003-38168, Atlanta, Georgia, USA.Google Scholar
Strahle, W. C. 1972 Some results in combustion generated noise. J. Sound Vib. 23 (1), 113–125.Google Scholar
Tripathy, S. C., Jain, K. & Bhatnagar, A. 2000 Helioseismic solar cycle changes and splitting coefficients. J. Astrophys. Astron. 21, 349–352.Google Scholar
Wolf, P., Staffelbach, G., Gicquel, L. Y. M., Muller, J. D. & Poinsot, T. 2012 Acoustic and large eddy simulation studies of azimuthal modes in annular combustion chambers. Combust. Flame 159, 3398–3413.Google Scholar
Wolf, P., Staffelbach, G., Roux, A., Gicquel, L., Poinsot, T. & Moureau, V. 2009 Massively parallel LES of azimuthal thermo-acoustic instabilities in annular gas turbines. C. R. Acad. Sci. Méc. 337 (6–7), 385–394.Google Scholar
Worth, N. A. & Dawson, J. R. 2013a Modal dynamics of self-excited azimuthal instabilities in an annular combustion chamber. Combust. Flame 160 (11), 2476–2489.Google Scholar
Worth, N. A. & Dawson, J. R. 2013b Self-excited cricumferential instabilities in a model annular gas turbine combustor: global flame dynamics. Proc. Combust. Inst. 34, 3127–3134.Google Scholar