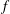Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-19T18:51:10.509Z Has data issue: false hasContentIssue false
  • English
  • Français

Symmetric and asymmetric inertial instability of zonal jets on the $f$-plane with complete Coriolis force

Published online by Cambridge University Press:  05 January 2016

Marine Tort ,
Bruno Ribstein  and
Vladimir Zeitlin
Marine Tort*
Affiliation:
Laboratoire de Météorologie Dynamique, Université Pierre et Marie Curie, École Normale Supérieure and École Polytechnique, 91120 Palaiseau, France
Bruno Ribstein
Affiliation:
Institut für Atmosphäre und Umwelt, Johann Wolfgang Goethe Universität Frankfurt, 60438 Frankfurt-am-Main, Germany
Vladimir Zeitlin
Affiliation:
Laboratoire de Météorologie Dynamique, Université Pierre et Marie Curie, École Normale Supérieure and École Polytechnique, 91120 Palaiseau, France Institut Universitaire de France, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Symmetric and asymmetric inertial instability of the westerly mid-latitude barotropic Bickley jet is analysed without the traditional approximation which neglects the vertical component of the Coriolis force, as well as the contribution of the vertical velocity to the latter. A detailed linear stability analysis of the jet at large Rossby numbers on the non-traditional 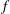$f$-plane is performed for long waves in both the two-layer rotating shallow-water and continuously stratified Boussinesq models. The dependence of the instability on both the Rossby and Burger numbers of the jet is investigated and compared to the traditional case. It is shown that non-traditional effects significantly increase the growth rate of the instability at small enough Burger numbers (weak stratifications) for realistic aspect ratios of the jet. The main results are as follows. (i) Two-layer shallow-water model. In the parameter regimes where the jet is inertially stable on the traditional 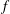$f$-plane, the symmetric inertial instability with respect to perturbations with zero along-jet wavenumber arises on the non-traditional 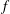$f$-plane. Both non-traditional symmetric and asymmetric (small but non-zero wavenumbers) inertial instabilities have higher growth rates than their traditional counterparts. (ii) Continuously stratified model. It is shown that by a proper change of variables the linear stability problem for the barotropic jet, on the non-traditional 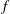$f$-plane, can be rendered separable and analysed along the same lines as in the traditional approximation. Neutral, weak and strong background stratifications are considered. For the neutral stratification the jet is inertially unstable if the traditional approximation is relaxed, while its traditional counterpart is not. For a sufficiently weak stratification, both symmetric and asymmetric inertial instabilities have substantially higher growth rates than in the traditional approximation. The across-jet structure of non-traditional unstable modes is strikingly different, as compared to those under the traditional approximation. No discernible differences between the two approximations are observed for strong enough stratifications. The influence of dissipation and non-hydrostatic effects upon the instability is quantified.

JFM classification

Instability: Instability Geophysical and Geological Flows: Rotating flows Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 788 , 10 February 2016 , pp. 274 - 302
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bjerknes, V., Bjerknes, J., Solberg, H. & Bergeron, T. 1933 Physikalische Hydrodynamik, mit Anwendung auf die Dynamische Meteorologie. Springer.Google Scholar
Bouchut, F., Ribstein, B. & Zeitlin, V. 2011 Inertial, barotropic, and baroclinic instabilities of the Bickley jet in two-layer rotating shallow-water model. Phys. Fluids 23 (12), 126601.Google Scholar
Boyd, J. P. 2000 Chebyshev and Fourier Spectral Methods. Dover.Google Scholar
Colin de Verdière, A. 2012 The stability of short symmetric internal waves on sloping fronts: beyond the traditional approximation. J. Phys. Oceanogr. 42, 459–475.Google Scholar
Colin de Verdière, A. & Schopp, R. 1994 Flows in a rotating spherical shell: the equatorial case. J. Fluid Mech. 276, 233–260.CrossRefGoogle Scholar
Dellar, P. J. 2011 Variations on a ${\it\beta}$ -plane: derivation of non-traditional ${\it\beta}$ -plane equations from Hamilton’s principle on a sphere. J. Fluid Mech. 674, 174–195.Google Scholar
Dunkerton, T. J. 1983 A nonsymmetric equatorial inertial instability. J. Atmos. Sci. 40 (3), 807–813.2.0.CO;2>CrossRefGoogle Scholar
Eckart, C. 1960 Hydrodynamics of Oceans and Atmospheres. Pergamon.Google Scholar
Emanuel, K. A. 1979 Inertial instability and mesoscale convective systems. Part I: Linear theory of inertial instability in rotating viscous fluids. J. Atmos. Sci. 36 (12), 2425–2449.Google Scholar
Fruman, M. D. & Shepherd, T. G. 2008 Symmetric stability of compressible zonal flows on a generalized equatorial ${\it\beta}$ -plane. J. Atmos. Sci. 65 (6), 1927–1940.CrossRefGoogle Scholar
Gerkema, T. & Shrira, V. I. 2005 Near-inertial waves in the ocean: beyond the traditional approximation. J. Fluid Mech. 529, 195–219.Google Scholar
Gerkema, T., Zimmerman, J. T. F., Maas, L. R. M. & Van Haren, H. 2008 Geophysical and astrophysical fluid dynamics beyond the traditional approximation. Rev. Geophys. 46 (2), RG2004.Google Scholar
Griffiths, S. D. 2003a The nonlinear evolution of zonally symmetric equatorial inertial instability. J. Fluid Mech. 474, 245–273.Google Scholar
Griffiths, S. D. 2003b Nonlinear vertical scale selection in equatorial inertial instability. J. Atmos. Sci. 60 (7), 977–990.Google Scholar
Griffiths, S. D. 2008 The limiting form of inertial instability in geophysical flows. J. Fluid Mech. 605, 115–143.CrossRefGoogle Scholar
Hayashi, H., Shiotani, M. & Gille, J. C. 1998 Vertically stacked temperature disturbances near the equatorial stratopause as seen in cryogenic limb array etalon spectrometer data. J. Geophys. Res. 103 (D16), 19469–19483.CrossRefGoogle Scholar
Hayashi, M. & Itoh, H. 2012 The importance of the non-traditional Coriolis terms in large-scale motions in the tropics forced by prescribed cumulus heating. J. Atmos. Sci. 69 (9), 2699–2716.Google Scholar
Hendershott, M. C. 1981 Long waves and ocean tides. In Evolution of Physical Oceanography. Scientific Surveys in Honor of Henry Stommel (ed. Warren, B. A. & Wunsch, C.), pp. 292–341. MIT.Google Scholar
Hoskins, B. J. & Bretherton, F. P. 1972 Atmospheric frontogenesis models: mathematical formulation and solution. J. Atmos. Sci. 29 (1), 11–37.Google Scholar
Hua, B. L., Moore, D. W. & Le Gentil, S. 1997 Inertial nonlinear equilibration of equatorial flows. J. Fluid Mech. 331, 345–371.Google Scholar
Kloosterziel, R. C. & Carnevale, G. F. 2008 Vertical scale selection in inertial instability. J. Fluid Mech. 594, 249–269.CrossRefGoogle Scholar
Kloosterziel, R. C., Carnevale, G. F. & Orlandi, P. 2007a Inertial instability in rotating and stratified fluids: barotropic vortices. J. Fluid Mech. 583, 379–412.Google Scholar
Kloosterziel, R. C., Orlandi, P. & Carnevale, G. F. 2007b Saturation of inertial instability in rotating planar shear flows. J. Fluid Mech. 583, 413–422.CrossRefGoogle Scholar
Kloosterziel, R. C., Orlandi, P. & Carnevale, G. F. 2015 Saturation of equatorial inertial instability. J. Fluid Mech. 767, 562–594.CrossRefGoogle Scholar
Laplace, P. S.1799–1825 Traité de la Mécanique Céleste (ed. J. B. M. Duprat). Paris.Google Scholar
Maas, L. R. M. 2001 Wave focusing and ensuing mean flow due to symmetry breaking in rotating fluids. J. Fluid Mech. 437, 13–28.Google Scholar
Müller, R. 1989 A note on the relation between the traditional approximation and the metric of the primitive equations. Tellus A 41A (2), 175–178.Google Scholar
Phillips, N. A. 1966 The equations of motion for a shallow rotating atmosphere and the ‘traditional approximation’. J. Atmos. Sci. 23 (5), 626–628.Google Scholar
Phillips, N. A. 1968 Reply. J. Atmos. Sci. 25 (6), 1155–1157.2.0.CO;2>CrossRefGoogle Scholar
Plougonven, R. & Zeitlin, V. 2005 Lagrangian approach to geostrophic adjustment of frontal anomalies in a stratified fluid. Geophys. Astrophys. Fluid Dyn. 99 (2), 101–135.CrossRefGoogle Scholar
Plougonven, R. & Zeitlin, V. 2009 Nonlinear development of inertial instability in a barotropic shear. Phys. Fluids 21 (10), 106601.Google Scholar
Reznik, G. M. 2014 Geostrophic adjustment with gyroscopic waves: stably neutrally stratified fluid without the traditional approximation. J. Fluid Mech. 747, 605–634.Google Scholar
Ribstein, B., Plougonven, R. & Zeitlin, V. 2014a Inertial versus baroclinic instability of the Bickley jet in continuously stratified rotating fluid. J. Fluid Mech. 743, 1–31.Google Scholar
Ribstein, B., Zeitlin, V. & Tissier, A.-S. 2014b Barotropic, baroclinic, and inertial instabilities of the easterly Gaussian jet on the equatorial ${\it\beta}$ -plane in rotating shallow water model. Phys. Fluids 26 (5), 056605.CrossRefGoogle Scholar
Sakai, S. 1989 Rossby–Kelvin instability: a new type of ageostrophic instability caused by a resonance between Rossby waves and gravity waves. J. Fluid Mech. 202, 174–195.CrossRefGoogle Scholar
Shrira, V. I. & Townsend, W. A. 2010 Deep ocean mixing by near-inertial waves. In IUTAM Symposium on Turbulence in the Atmosphere and Oceans (ed. Dritschel, D.), IUTAM Bookseries, vol. 28, pp. 63–73. Springer.Google Scholar
Shrira, V. I. & Townsend, W. A. 2013 Near-inertial waves and deep ocean mixing. Phys. Scr. 2013 (T155), 014036.Google Scholar
Stewart, A. L. & Dellar, P. J. 2010 Two-layer shallow water equations with complete Coriolis force and topography. In Progress in Industrial Mathematics at ECMI 2008 (ed. Fitt, A. D., Norbury, J., Ockendon, H. & Wilson, E.), Mathematics in Industry, vol. 1, pp. 1033–1038. Springer.Google Scholar
Stewart, A. L. & Dellar, P. J. 2011a Cross-equatorial flow through an abyssal channel under the complete Coriolis force: two-dimensional solutions. Ocean Model. 40 (1), 87–104.Google Scholar
Stewart, A. L. & Dellar, P. J. 2011b The role of the complete Coriolis force in cross-equatorial flow of abyssal ocean currents. Ocean Model. 38 (3–4), 187–202.Google Scholar
Sun, W.-Y. 1995 Unsymmetrical symmetric instability. Q. J. R. Meteorol. Soc. 121 (522), 419–431.Google Scholar
Tort, M. & Dubos, T. 2014 Dynamically consistent shallow-atmosphere equations with a complete Coriolis force. Q. J. R. Meteorol. Soc. 140, 2388–2392.Google Scholar
Tort, M., Dubos, T., Bouchut, F. & Zeitlin, V. 2014 Consistent shallow-water equations on the rotating sphere with complete Coriolis force and topography. J. Fluid Mech. 748, 789–821.Google Scholar
Trefethen, L. N. 2000 Spectral Methods in MATLAB. SIAM.Google Scholar
White, A. A. & Bromley, R. A. 1995 Dynamically consistent, quasi-hydrostatic equations for global models with a complete representation of the Coriolis force. Q. J. R. Meteorol. Soc. 121 (522), 399–418.Google Scholar
Winters, K. B., Bouruet-Aubertot, P. & Gerkema, T. 2011 Critical reflection and abyssal trapping of near-inertial waves on a ${\it\beta}$ -plane. J. Fluid Mech. 684, 111–136.Google Scholar
Zeitlin, V., Medvedev, S. & Plougonven, R. 2003 Frontal geostrophic adjustment, slow manifold and nonlinear wave phenomena in one-dimensional rotating shallow water. Part 1. Theory. J. Fluid Mech. 481, 269–290.Google Scholar