Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Li, Gaojin
and
Koch, Donald L.
2022.
Dynamics of a self-propelled compound droplet.
Journal of Fluid Mechanics,
Vol. 952,
Issue. ,
Farutin, A.
Rizvi, M.S.
Hu, W.-F.
Lin, T.S.
Rafaï, S.
and
Misbah, C.
2022.
A reduced model for a phoretic swimmer.
Journal of Fluid Mechanics,
Vol. 952,
Issue. ,
Suda, Saori
Suda, Tomoharu
Ohmura, Takuya
and
Ichikawa, Masatoshi
2022.
Motion of a swimming droplet under external perturbations: A model-based approach.
Physical Review E,
Vol. 106,
Issue. 3,
Kailasham, R.
and
Khair, Aditya S.
2022.
Dynamics of forced and unforced autophoretic particles.
Journal of Fluid Mechanics,
Vol. 948,
Issue. ,
Dwivedi, Prateek
Shrivastava, Atishay
Pillai, Dipin
Tiwari, Naveen
and
Mangal, Rahul
2023.
Deforming active droplets in viscoelastic solutions.
Soft Matter,
Vol. 19,
Issue. 21,
p.
3783.
Mo, Chaojie
Li, Gaojin
and
Bian, Xin
2023.
Challenges and attempts to make intelligent microswimmers.
Frontiers in Physics,
Vol. 11,
Issue. ,
Kailasham, R.
and
Khair, Aditya S.
2023.
Non-Brownian diffusion and chaotic rheology of autophoretic disks.
Physical Review E,
Vol. 107,
Issue. 4,
Zhu, Guangpu
and
Zhu, Lailai
2023.
Self-propulsion of an elliptical phoretic disk emitting solute uniformly.
Journal of Fluid Mechanics,
Vol. 974,
Issue. ,
Dwivedi, Prateek
Shrivastava, Atishay
Pillai, Dipin
and
Mangal, Rahul
2023.
Mode switching of active droplets in macromolecular solutions.
Soft Matter,
Vol. 19,
Issue. 22,
p.
4099.
Schnitzer, Ory
2023.
Weakly nonlinear dynamics of a chemically active particle near the threshold for spontaneous motion. I. Adjoint method.
Physical Review Fluids,
Vol. 8,
Issue. 3,
Brandão, Rodolfo
and
Yariv, Ehud
2023.
Spontaneous autophoretic motion of isotropic disks.
Journal of Fluid Mechanics,
Vol. 972,
Issue. ,
Yang, Qianhong
Jiang, Maoqiang
Picano, Francesco
and
Zhu, Lailai
2024.
Shaping active matter from crystalline solids to active turbulence.
Nature Communications,
Vol. 15,
Issue. 1,
Song, Chunlei
Tao, Xianzan
Chen, Yicheng
Mao, Kaihao
Tao, Ye
Ge, Zhenyou
Wen, Hongyan
Chen, Gaofeng
Li, Biao
Xue, Rui
Jiang, Xikai
Zheng, Xu
and
Ren, Yukun
2024.
Electrocapillarity‐Induced Hurricane‐in‐a‐Tube Enables the Generation and Patterning of Liquid Metal Droplets.
Advanced Functional Materials,
Vol. 34,
Issue. 49,
Fuchs, Richard
Abdoli, Shiva
Kilani, Mohamed
Nor‐Azman, Nur‐Adania
Yu, Ruohan
Tang, Shi‐Yang
Dickey, Michael D.
Mao, Guangzhao
Kalantar‐Zadeh, Kourosh
and
Tang, Jianbo
2024.
Stroking through Electrolyte: Liquid Metal Droplet Propulsion through Pulse Time Modulation.
Advanced Functional Materials,
Vol. 34,
Issue. 17,
Ray, Swarnak
and
Roy, Arun
2024.
Experimental studies on self-propulsion of deformable 5CB liquid crystal droplets in micellar solution.
Liquid Crystals,
Vol. 51,
Issue. 8-9,
p.
1578.
Chen, Yibo
Chong, Kai Leong
Liu, Haoran
Verzicco, Roberto
and
Lohse, Detlef
2024.
Buoyancy-driven attraction of active droplets.
Journal of Fluid Mechanics,
Vol. 980,
Issue. ,
Farutin, Alexander
and
Misbah, Chaouqi
2024.
Singular bifurcations and regularization theory.
Physical Review E,
Vol. 109,
Issue. 6,
Crowdy, Darren G.
2024.
Viscous Marangoni migration of an inviscid bubble by surfactant spreading: an exactly solvable model.
Journal of Fluid Mechanics,
Vol. 1000,
Issue. ,
Roy, Rahul
and
Mandal, Shubhadeep
2025.
Chemically active particles in extensional flow.
Journal of Fluid Mechanics,
Vol. 1008,
Issue. ,
 $Pe$) and Damköhler number (
$Pe$) and Damköhler number ( $Da$). The weakly nonlinear analysis shows that near the instability threshold, the drop undergoes a supercritical bifurcation with velocity
$Da$). The weakly nonlinear analysis shows that near the instability threshold, the drop undergoes a supercritical bifurcation with velocity  $U\sim \sqrt {Pe-Pe_c}$, where
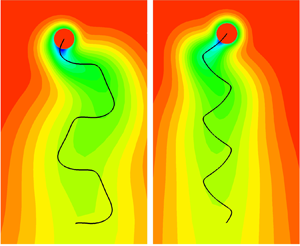
$U\sim \sqrt {Pe-Pe_c}$, where  $Pe_c$ is the critical Péclet number for the onset of dipole mode. In the highly nonlinear regime, the drop transits from steady translation of pusher swimming to unsteady motion of mixed pusher–puller swimming along zigzaging trajectories of quadrangle and/or triangle waves. Mode decomposition shows that the zigzag motion is directly related to the interaction between the secondary wake of low surfactant concentration and the primary wake.
$Pe_c$ is the critical Péclet number for the onset of dipole mode. In the highly nonlinear regime, the drop transits from steady translation of pusher swimming to unsteady motion of mixed pusher–puller swimming along zigzaging trajectories of quadrangle and/or triangle waves. Mode decomposition shows that the zigzag motion is directly related to the interaction between the secondary wake of low surfactant concentration and the primary wake.