Published online by Cambridge University Press: 12 January 2012
In this paper, we conduct a numerical investigation of sheared suspensions of non-colloidal spherical particles on which a torque is applied. Particles are mono-dispersed and neutrally buoyant. Since the torque modifies particle rotation, we show that it can indeed strongly change the effective viscosity of semi-dilute or even more concentrated suspensions. We perform our calculations up to a volume fraction of 28 %. And we compare our results to data obtained at 40 % by Yeo and Maxey (Phys. Rev. E, vol. 81, 2010, p. 62501) with a totally different numerical method. Depending on the torque orientation, one can increase (decrease) the rotation of the particles. This results in a strong enhancement (reduction) of the effective shear viscosity of the suspension. We construct a dimensionless number 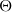 which represents the average relative angular velocity of the particles divided by the vorticity of the fluid generated by the shear flow. We show that the contribution of the particles to the effective viscosity can be suppressed for a given and unique value of
which represents the average relative angular velocity of the particles divided by the vorticity of the fluid generated by the shear flow. We show that the contribution of the particles to the effective viscosity can be suppressed for a given and unique value of 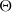 independently of the volume fraction. In addition, we obtain a universal behaviour (i.e. independent of the volume fraction) when we plot the relative effective viscosity divided by the relative effective viscosity without torque as a function of
independently of the volume fraction. In addition, we obtain a universal behaviour (i.e. independent of the volume fraction) when we plot the relative effective viscosity divided by the relative effective viscosity without torque as a function of 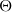 . Finally, we show that a modified Faxén law can be equivalently established for large concentrations.
. Finally, we show that a modified Faxén law can be equivalently established for large concentrations.