Hostname: page-component-66644f4456-q629f Total loading time: 0 Render date: 2025-02-12T20:57:32.304Z Has data issue: true hasContentIssue false
  • English
  • Français

Suspension flow through an asymmetric T-junction

Published online by Cambridge University Press:  04 April 2018

Sojwal Manoorkar Open the ORCID record for Sojwal Manoorkar [Opens in a new window] ,
Sreenath Krishnan ,
Omer Sedes ,
Eric S. G. Shaqfeh ,
Gianluca Iaccarino  and
Jeffrey F. Morris
Sojwal Manoorkar
Affiliation:
Benjamin Levich Institute and Department of Chemical Engineering, The City College of New York, New York, NY 10031, USA
Sreenath Krishnan
Affiliation:
Department of Mechanical Engineering, Stanford University, Stanford, CA 94305, USA
Omer Sedes
Affiliation:
Benjamin Levich Institute and Department of Chemical Engineering, The City College of New York, New York, NY 10031, USA
Eric S. G. Shaqfeh
Affiliation:
Department of Mechanical Engineering, Stanford University, Stanford, CA 94305, USA Department of Chemical Engineering, Stanford University, Stanford, CA 94305, USA Institute for Computational and Mathematical Engineering, Stanford University, Stanford, CA 94305, USA
Gianluca Iaccarino
Affiliation:
Department of Mechanical Engineering, Stanford University, Stanford, CA 94305, USA
Jeffrey F. Morris*
Affiliation:
Benjamin Levich Institute and Department of Chemical Engineering, The City College of New York, New York, NY 10031, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The flow of a suspension through a bifurcating channel is studied experimentally and by computational methods. The geometry considered is an ‘asymmetric T’, as flow in the entering branch divides to either continue straight or to make a right angle turn. All branches are of the same square cross-section of side length 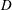$D$, with inlet and outlet section lengths 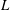$L$ yielding 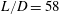$L/D=58$ in the experiments. The suspensions are composed of neutrally buoyant spherical particles in a Newtonian liquid, with mean particle diameters of 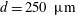$d=250~\unicode[STIX]{x03BC}\text{m}$ and 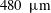$480~\unicode[STIX]{x03BC}\text{m}$ resulting in 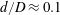$d/D\approx 0.1$ to 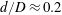$d/D\approx 0.2$ for 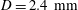$D=2.4~\text{mm}$. The flow rate ratio 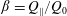$\unicode[STIX]{x1D6FD}=Q_{\Vert }/Q_{0}$, defined for the bulk, fluid and particles, is used to characterize the flow behaviour; here 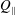$Q_{\Vert }$ and 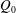$Q_{0}$ are volumetric flow rates in the straight outlet branch and inlet branch, respectively. The channel Reynolds number 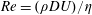$Re=(\unicode[STIX]{x1D70C}DU)/\unicode[STIX]{x1D702}$ was varied over 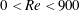$0<Re<900$, with 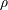$\unicode[STIX]{x1D70C}$ and 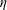$\unicode[STIX]{x1D702}$ the fluid density and viscosity, respectively, and 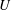$U$ the mean velocity in the inlet channel; the inlet particle volume fraction was 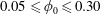$0.05\leqslant \unicode[STIX]{x1D719}_{0}\leqslant 0.30$. Experimental and numerical results for single-phase Newtonian fluid both show 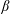$\unicode[STIX]{x1D6FD}$ increasing with 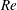$Re$, implying more material tending toward the straight branch as the inertia of the flow increases. In suspension flow at small 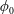$\unicode[STIX]{x1D719}_{0}$, inertial migration of particles in the inlet branch affects the flow rate ratio for particles (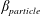$\unicode[STIX]{x1D6FD}_{\mathit{particle}}$) and suspension (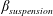$\unicode[STIX]{x1D6FD}_{\mathit{suspension}}$). The flow split for the bulk suspension satisfies 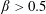$\unicode[STIX]{x1D6FD}>0.5$ for 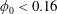$\unicode[STIX]{x1D719}_{0}<0.16$ while 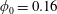$\unicode[STIX]{x1D719}_{0}=0.16$ crosses from 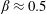$\unicode[STIX]{x1D6FD}\approx 0.5$ to 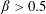$\unicode[STIX]{x1D6FD}>0.5$ at 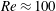$Re\approx 100$. For 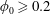$\unicode[STIX]{x1D719}_{0}\geqslant 0.2$, 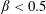$\unicode[STIX]{x1D6FD}<0.5$ at all 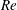$Re$ studied. A complex dependence of the mean solid fraction in the downstream branches upon inlet fraction $\unicode[STIX]{x1D719}_{0}$ and 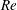$Re$ is observed: for 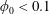$\unicode[STIX]{x1D719}_{0}<0.1$, the solid fraction in the straight downstream branch initially decreases with 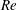$Re$, before increasing to surpass the inlet fraction at large 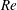$Re$ (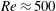$Re\approx 500$ for 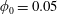$\unicode[STIX]{x1D719}_{0}=0.05$). At 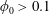$\unicode[STIX]{x1D719}_{0}>0.1$, the solid fraction in the straight branch satisfies 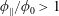$\unicode[STIX]{x1D719}_{\Vert }/\unicode[STIX]{x1D719}_{0}>1$, and this ratio grows with 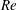$Re$. Discrete-particle simulations employing immersed boundary and lattice-Boltzmann techniques are used to analyse these phenomena, allowing rationalization of aspects of this complex behaviour as being due to particle migration in the inlet branch.

JFM classification

Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Complex Fluids: Suspensions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 844 , 10 June 2018 , pp. 247 - 273
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahmed, G. M. Y. & Singh, A. 2011 Numerical simulation of particle migration in asymmetric bifurcation channel. J. Non-Newtonian Fluid Mech. 166, 42–51.10.1016/j.jnnfm.2010.10.004Google Scholar
Aidun, C. K., Lu, Y. & Ding, J.-E. 1998 Direct analysis of particulate suspensions with inertia using the discrete Boltzmann equation. J. Fluid Mech. 373, 287–311.10.1017/S0022112098002493Google Scholar
Asmolov, E. S. 1999 The inertial lift on a spherical particle in a plane Poiseuille flow at a large channel Reynolds number. J. Fluid Mech. 381, 63–87.10.1017/S0022112098003474Google Scholar
Bhagat, A. A. S., Kuntaegowdanahalli, S. S. & Papautsky, I. 2008 Enhanced particle filtration in straight microchannels using shear-modulated inertial migration. Phys. Fluids 20, 101702.10.1063/1.2998844Google Scholar
Boyer, F., Pouliquen, Q. & Guazzelli, E. 2011 Dense suspension in rotating-rod flows: normal stresses and particle migration. J. Fluid Mech. 686, 5–25.10.1017/jfm.2011.272Google Scholar
Bugliarello, G. & Hsiao, G. C. C. 1964 Phase separation in suspensions flowing through bifurcations: a simplified hemodynamic model. Science 143 (3605), 469–471.10.1126/science.143.3605.469Google Scholar
Chun, B. & Ladd, A. C. J. 2006 Inertial migration of neutrally buoyant particles in a square duct: an investigation of multiple equilibrium positions. Phys. Fluids 18, 031704.10.1063/1.2176587Google Scholar
Deboeuf, A., Gauthier, G., Martin, J., Yurkovetsky, Y. & Morris, J. F. 2009 Particle pressure in a sheared suspension: a bridge from osmosis to granular dilatancy. Phys. Rev. Lett. 102, 108301.10.1103/PhysRevLett.102.108301Google Scholar
Doyeux, V., Podgorski, T., Peponas, S., Ismail, M. & Coupier, G. 2011 Spheres in the vicinity of a bifurcation: elucidating the Zweifach-Fung effect. J. Fluid Mech. 674, 359–388.10.1017/S0022112010006567Google Scholar
Einstein, A. 1906 Eine neue Bestimmung der Moleküldimensionen. Ann. Phys. (4) 19, 289–306.10.1002/andp.19063240204Google Scholar
Enden, G. & Popel, A. S. 1994 A numerical study of plasma skimming in small vascular bifurcations. Trans. ASME J. Biomech. Engng 116 (1), 79–88.10.1115/1.2895708Google Scholar
Garagash, D., Lecampion, B. & Desroches, J. 2015 Pressure-driven suspension flow near jamming. Phys. Rev. Lett. 114, 088301.Google Scholar
Garagash, D. I. & Lecampion, B. 2014 Confined flow of suspension modeled by a frictional rheology. J. Fluid Mech. 759, 197–235.Google Scholar
Glowinski, R., Pan, T. W., Hesla, T. I., Joseph, D. D. & Periaux, J. 2001 A fictitious domain approach to the direct numerical simulation of incompressible viscous flow past moving rigid bodies: application to particulate flow. J. Comput. Phys. 169 (2), 363–426.10.1006/jcph.2000.6542Google Scholar
Guazzelli, É. & Morris, J. F. 2012 A Physical Introduction to Suspension Dynamics. Cambridge University Press.Google Scholar
Haddadi, H. & Morris, J. F. 2014 Microstructure and rheology of finite inertia neutrally buoyant suspensions. J. Fluid Mech. 749, 431–459.10.1017/jfm.2014.238Google Scholar
Haddadi, H., Shojaei-Zadeh, S. & Morris, J. F. 2016 Lattice-Boltzmann simulation of inertial particle-laden flow around an obstacle. Phys. Rev. Fluids 1, 024201.10.1103/PhysRevFluids.1.024201Google Scholar
Ham, F. 2007 An efficient scheme for large eddy simulation of low-Ma combustion in complex configurations. In Annu. Res. Briefs, p. 41. Center for Turbulence Research, Stanford University.Google Scholar
Ham, F., Mattsson, K. & Iaccarino, G. 2006 Accurate and stable finite volume operators for unstructured flow solvers. In Annu. Res. Briefs, pp. 243–261. Center for Turbulence Research, Stanford University.Google Scholar
Hampton, R. E., Mammoli, A. A., Graham, A. L., Tetlow, W. & Altobelli, S. A. 1997 Migration of particles undergoing pressure-driven flow in a circular conduit. J. Rheol. 41, 621–640.10.1122/1.550863Google Scholar
Han, M., Kim, C., Kim, M. & Lee, S. 1999 Particle migration in tube flow of suspesnsion. J. Rheol. 43 (197), 1157–1174.10.1122/1.551019Google Scholar
Ho, B. P. & Leal, L. G. 1974 Inertial migration of rigid spheres in two-dimensional unidirectional flow. J. Fluid Mech. 65, 365–400.10.1017/S0022112074001431Google Scholar
Iwanami, S. & Suu, T. 1969 Study on flow characteristics in right-angled pipe fittings. Bull. JSME 12 (53), 1051–1061.10.1299/jsme1958.12.1051Google Scholar
Kempe, T. & Fröhlich, J. 2012a Collision modelling for the interface-resolved simulation of spherical particles in viscous fluids. J. Fluid Mech. 709, 445–489.10.1017/jfm.2012.343Google Scholar
Kempe, T. & Fröhlich, J. 2012b An improved immersed boundary method with direct forcing for the simulation of particle laden flows. J. Comput. Phys. 231 (9), 3663–3684.10.1016/j.jcp.2012.01.021Google Scholar
Koh, C. J., Hookham, P. & Leal, L. G. 1994 An experimental investigation of concentrated suspension flows in a rectangular channel. J. Fluid Mech. 266, 1–32.10.1017/S0022112094000911Google Scholar
Krieger, I. M. 1972 Rheology of monodisperse lattices. Adv. Colloid Interface Sci. 3 (2), 111–136.10.1016/0001-8686(72)80001-0Google Scholar
Krishnan, S., Shaqfeh, E. S. G. & Iaccarino, G. 2017 Fully resolved viscoelastic particulate simulations using unstructured grids. J. Comput. Phys. 338, 313–338.10.1016/j.jcp.2017.02.068Google Scholar
Kulkarni, P. M., Manoorkar, S., Morris, J. F. & Tonmukayakul, N.2016 Determining flow through a fracture junction in a complex fracture network. US Patent 9,418,184.Google Scholar
Ladd, A. J. C. 1994a Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 1. Theoretical foundation. J. Fluid Mech. 21, 285–309.10.1017/S0022112094001771Google Scholar
Ladd, A. J. C. 1994b Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 2. Numerical results. J. Fluid Mech. 271, 311–339.10.1017/S0022112094001783Google Scholar
Lashgari, I., Picano, F., Breugem, W. P. & Brandt, L. 2016 Channel flow of rigid sphere suspensions: particle dynamics in the inertial regime. Intl J. Multiphase Flow 78, 12–24.10.1016/j.ijmultiphaseflow.2015.09.008Google Scholar
Liepsch, D. & Moravec, S. 1982 Measurement and calculations of laminar flow in a ninety degree bifurcation. J. Biomech. 15 (7), 473–485.10.1016/0021-9290(82)90001-XGoogle Scholar
Matas, J. P., Morris, J. F. & Guazzelli, E. 2004 Inertial migration of rigid spherical particles in Poiseuille flow. J. Fluid Mech. 515, 171–195.10.1017/S0022112004000254Google Scholar
Matas, J. P., Morris, J. F. & Guazzelli, E. 2009 Lateral force on a rigid sphere in large-inertia laminar pipe flow. J. Fluid Mech. 621, 59–67.10.1017/S0022112008004977Google Scholar
Mittal, R. & Iaccarino, G. 2005 Immersed boundary methods. Annu. Rev. Fluid Mech. 37, 239–261.10.1146/annurev.fluid.37.061903.175743Google Scholar
Miura, K., Itano, T. & Sugihara-Seki, M. 2014 Inertial migration of neutrally buoyant spheres in a pressure-driven flow through square channels. J. Fluid Mech. 749, 320–330.10.1017/jfm.2014.232Google Scholar
Morris, J. F. & Boulay, F. 1999 Curvilinear flows of noncolloidal suspensions: the role of normal stresses. Soc. Rheol. 48 (5), 1213–1237.10.1122/1.551021Google Scholar
Morris, J. F. 2009 A review of microstructure in concentrated suspensions and its implications for rheology and bulk flow. Rheol. Acta 48, 909–923.10.1007/s00397-009-0352-1Google Scholar
Moshkin, N. & Yambangwi, D. 2009 Steady viscous incompressible flow driven by a pressure difference in a planar T-junction channel. Intl J. Comput. Fluid Dyn. 23 (3), 259–270.10.1080/10618560902815204Google Scholar
Neary, V. S. & Sotiropoulos, F. 1996 Numerical investigation of laminar flows through 90-degree diversions of rectangular cross-section. Comput. Fluids 25 (2), 95–118.10.1016/0045-7930(95)00030-5Google Scholar
Nguyen, N.-Q. & Ladd, A. 2002 Lubrication corrections for lattice-Boltzmann simulations of particle suspensions. Phys. Rev. E 66 (4), 04708.Google Scholar
Nott, P. R. & Brady, J. F. 1994 Pressure-driven flow of suspensions: simulation and theory. J. Fluid Mech. 275, 157–199.10.1017/S0022112094002326Google Scholar
Pedley, T. J. 2008 The Fluid Mechanics of Large Blood Vessels. Cambridge University Press.Google Scholar
Pries, A. R., Secomb, P., Gaehtgens, P. & Gross, J. F. 1990 Blood flow in microvascular networks. Circulat. Res. 67, 826–834.10.1161/01.RES.67.4.826Google Scholar
Roberts, B. W. & Olbricht, W. L. 2006 Flow-induced particulate separations. AIChE J. 49 (11), 2842–2849.10.1002/aic.690491116Google Scholar
Roscoe, R. 1952 The viscosity of suspension of rigid spheres. Brit. J. Appl. Phys. 3, 267–269.10.1088/0508-3443/3/8/306Google Scholar
Rubinow, S. I. & Keller, J. B. 1961 The transverse force on a spinning sphere moving in a viscous fluid. J. Fluid Mech. 11, 447–459.10.1017/S0022112061000640Google Scholar
Saffman, P. G. 1965 The lift on a small sphere in a slow shear flow. J. Fluid Mech. 22, 385–400.10.1017/S0022112065000824Google Scholar
Schonberg, J. A. & Hinch, E. J. 1989 Inertial migration of a sphere in Poiseuille flow. J. Fluid Mech. 203, 517–524.10.1017/S0022112089001564Google Scholar
Segré, G. & Silberberg, A. 1961 Radial particle displacements in Poiseuille flow of suspensions. Nature 189, 109–210.10.1038/189209a0Google Scholar
Shen, H. H., Satake, M., Mehrabadi, M., Chang, C. S. & Campbell, C. S.(Eds) 1992 Advances in Micromechanics of Granular Materials. Elsevier.Google Scholar
Warpinski, N. R., Mayerhofer, M. J., Vincet, M. C., Cipolla, C. L. & Lolon, E. P. 2009 Stimulating unconventional reservoirs: maximizing network growth while optimizing fracture conductivity. J. Can. Petrol. Technol. 48 (10), 39–51.10.2118/114173-PAGoogle Scholar
Xi, C. & Shapley, N. C. 2008 Flow of a concentrated suspension through an axisymmetric bifurcation. J. Rheol. 52 (2), 625–647.10.1122/1.2833469Google Scholar
Yan, Z.-Y., Acrivos, A. & Weinbaum, S. 1991 A three-dimensional analysis of plasma skimming at microvascular bifurcations. Microvasc. Res. 42 (1), 17–38.10.1016/0026-2862(91)90072-JGoogle Scholar
Zarraga, I. E., Hill, D. A. & Leighton, D. T. 2000 The characterization of the total stress of concentrated suspensions of noncolloidal spheres in Newtonian fluids. J. Rheol. 44, 185–220.10.1122/1.551083Google Scholar

Manoorkar et al. supplementary movie 1

Experiment at Φ0 = 0.05, d/D = 0.2, Re = 200. Video is 100 times slower than real time.

Download Manoorkar et al. supplementary movie 1(Video)
Video 5.7 MB

Manoorkar et al. supplementary movie 2

Immersed boundary simulation at Φ0 = 0.05, d/D = 0.2, Re = 200."The video shows the entry and bifurcation regions separately as well as the full channel view as the particles enter and reach a steady state flow.

Download Manoorkar et al. supplementary movie 2(Video)
Video 32.5 MB

Manoorkar et al. supplementary movie 3

Comparison of experiment and immersed boundary simulation in bifurcation region at Φ0 = 0.05, d/D = 0.2, Re = 300 for IB and Re = 311 for experiments.

Download Manoorkar et al. supplementary movie 3(Video)
Video 9.5 MB

Manoorkar et al. supplementary movie 4

Experiment at Φ0 = 0.05, d/D = 0.2, Re = 415. Video is 100 times slower than real time.

Download Manoorkar et al. supplementary movie 4(Video)
Video 6.3 MB

Manoorkar et al. supplementary movie 5

Comparison of experiment and immersed boundary simulation in bifurcation region at Φ0 = 0.05, d/D = 0.2, Re = 600 for IB and Re = 620 for experiments.

Download Manoorkar et al. supplementary movie 5(Video)
Video 6.1 MB

Manoorkar et al. supplementary movie 6

Experiment at Φ0 = 0.05, d/D = 0.2, Re = 830. Video is 100 times slower than real time.

Download Manoorkar et al. supplementary movie 6(Video)
Video 10.5 MB