Hostname: page-component-5f745c7db-8qdnt Total loading time: 0 Render date: 2025-01-06T20:54:02.282Z Has data issue: true hasContentIssue false
  • English
  • Français

Surfactant effect on path instability of a rising bubble

Published online by Cambridge University Press:  04 December 2013

Yoshiyuki Tagawa ,
Shu Takagi  and
Yoichiro Matsumoto
Yoshiyuki Tagawa*
Affiliation:
Department of Mechanical Engineering, School of Engineering, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-8656, Japan Department of Mechanical Systems Engineering, Tokyo University of Agriculture and Technology, 2-24-16 Nakacho, Koganei-city, Tokyo 184-8588, Japan
Shu Takagi
Affiliation:
Department of Mechanical Engineering, School of Engineering, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-8656, Japan
Yoichiro Matsumoto
Affiliation:
Department of Mechanical Engineering, School of Engineering, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-8656, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We report results from the first systematic experiments for investigating surfactant effects on path instability of an air bubble rising in quiescent water. The addition of surfactant to a gas–water system causes a non-uniform distribution of surfactant concentration along the bubble surface, resulting in variations in the gas–water boundary condition from zero shear stress to non-zero shear stress due to the Marangoni effect. This leads to retarded surface velocity and ends up with immobilization of the bubble surface with increasing surfactant concentration, where the drag corresponds to that of a solid sphere of the same size. 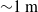Using two high-speed cameras and vertical traverse systems, we measure three-dimensional trajectories, velocities and aspect ratios of a millimetre-sized bubble simultaneously for ${\sim }1~\mathrm{m} $. Experimental parameters are the diameter of the bubble and the surfactant concentration of 1-Pentanol or Triton X-100. We explore the surfactant effect on the drag and lift forces acting on the bubble in helical motion. While the drag force monotonically increases with the surfactant concentration as expected, the lift force shows a non-monotonic behaviour. Nevertheless, the direction of the lift force in a reference frame that rotates with the bubble along its trajectory is kept almost constant. We also observe the transient trajectory starting from helical motion to zigzag, which has never been reported in the case of purified water. The instantaneous amplitude and frequency of the transient motion agree with those of the motion regarded as steady. Finally the bubble motions are categorized as straight/helical/zigzag and experimentally examined in the field of two dimensionless numbers: Reynolds number 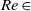$\mathit{Re}\in $ [300 900] and the normalized drag coefficient 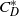${ C}_{D}^{\ast } $ which represents the slip condition. Remarkably it is found that the motions of a bubble with the intermediate slip conditions between free-slip and no-slip are helical for a broad range of 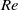$\mathit{Re}$.

JFM classification

Drops and Bubbles: Bubble dynamics Multiphase and Particle-laden Flows: Multiphase flow Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 738 , 10 January 2014 , pp. 124 - 142
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aybers, N. M. & Tapuku, A. 1969 The motion of gas bubbles rising through a stagnant liquid. Wärme-Stoffübertrag 2, 118–128.CrossRefGoogle Scholar
Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Brücker, C. 2001 Spatio-temporal reconstruction of vortex dynamics in axisymmetric wakes. J. Fluid Struct. 15, 543–554.Google Scholar
Chang, C. H. & Franses, E. I. 1995 Adsorption dynamics of surfactants at the air/water interface: a critical review of mathematical models, data, and mechanisms. Colloids Surf. A: Physicochem. Eng. Aspects 100, 1–45.Google Scholar
Clift, R., Grace, J. R. & Weber, M. E. 1978 Bubbles, Drops and Particles. Academic Press.Google Scholar
Cuenot, B., Magnaudet, J. & Spennato, B. 1997 The effects of slightly soluble surfactants on the flow around a spherical bubble. J. Fluid Mech. 339, 25–53.Google Scholar
Duineveld, P. C. 1995 The rise velocity and shape of bubbles in pure water at high Reynolds number. J. Fluid Mech. 292, 325–332.CrossRefGoogle Scholar
Eggleton, C. D., Pawar, Y. P. & Stebe, K. J. 1999 Insoluble surfactants on a drop in an extensional flow: a generalization of the stagnated surface limit to deforming interfaces. J. Fluid Mech. 385, 79–99.CrossRefGoogle Scholar
Ellingsen, K. & Risso, F. 2001 On the rise of an ellipsoidal bubble in water: oscillatory paths and liquid-induced velocity. J. Fluid Mech. 440, 235–268.Google Scholar
Ern, P., Risso, F., Fabre, D. & Magnaudet, J. 2012 Wake-induced oscillatory paths of bodies freely rising or falling in fluids. Annu. Rev. Fluid Mech. 44 (1), 97–121.CrossRefGoogle Scholar
Fainerman, V. B. & Lylyk, S. V. 1982 Dynamic surface tension and kinetics of adsorption in solutions of normal alcohols. Kolloidn. Z. 44, 538–544.Google Scholar
Fdhila, R. B. & Duineveld, P. C. 1996 The effect of surfactant on the rise of a spherical bubble at high Reynolds and Péclet numbers. Phys. Fluids 8, 310–321.Google Scholar
Frumkin, A. & Levich, V. G. 1947 On surfactants and interfacial motion. Zh. Fiz. Khim. 21, 1183–1204.Google Scholar
Fukuta, M., Takagi, S. & Matsumoto, Y. 2008 Numerical study on the shear-induced lift force acting on a spherical bubble in aqueous surfactant solutions. Phys. Fluids 20, 040704.Google Scholar
Haberman, W. L. & Morton, R. K. 1954 An experimental study of bubbles moving in liquids. Trans. ASCE 387, 227–252.Google Scholar
Hartunian, R. A. & Sears, W. R. 1957 On the instability of small gas bubbles moving uniformly in various liquids. J. Fluid Mech. 3 (01), 27–47.CrossRefGoogle Scholar
Howe, M. S. 1995 On the force and moment on a body in an incompressible fluid, with application to rigid bodies and bubbles at high and low Reynolds numbers. Q. J. Mech. Appl. Maths 48, 401–426.Google Scholar
Jachimska, B., Warszynski, P. & Malysa, K. 2001 Influence of adsorption kinetics and bubble motion on stability of the foam films formed at $n$ -octanol, $n$ -hexanol and $n$ -butanol solution surface. Colloids Surf. A: Physicochem. Eng. Aspects 192 (1), 177–193.Google Scholar
Jenny, M., Dusek, J. & Bouchet, G. 2004 Instabilities and transition of a sphere falling or ascending freely in a Newtonian fluid. J. Fluid Mech. 508, 201–239.Google Scholar
Kim, I. & Pearlstein, A. J. 1990 Stability of the flow past a sphere. J. Fluid Mech. 211, 73–93.Google Scholar
Krzan, M. & Malysa, K. 2002 Profiles of local velocities of bubbles in $n$ -butanol, $n$ -hexanol and $n$ -nonanol solutions. Colloids Surf. A: Physicochem. Eng. Aspects 207 (1), 279–291.Google Scholar
Leal, L. G. 1989 Vorticity transport and wake structure for bluff bodies at finite Reynolds number. Phys. Fluids A: Fluid Dyn. 1, 124–131.Google Scholar
Liao, Y. & McLaughlin, J. B. 2000 Bubble motion in aqueous surfactant solutions. J. Colloid Interface Sci. 224 (2), 297–310.Google Scholar
Lin, S. Y., McKeigue, K. & Maldarelli, C. 1990 Diffusion-controlled surfactant adsorption studied by pendant drop digitization. AIChE J. 36 (12), 1785–1795.CrossRefGoogle Scholar
Lunde, K. & Perkins, R. J. 1997 Observations on wakes behind spheroidal bubbles and particles. In 1997 ASME Fluids Engineering Division Summer Meeting, pp. 1–8.Google Scholar
Magnaudet, J. & Eames, I. 2000 The motion of high-Reynolds-number bubbles in inhomogeneous flows. Annu. Rev. Fluid Mech. 32 (1), 659–708.Google Scholar
Magnaudet, J. & Mougin, G. 2007 Wake instability of a fixed spheroidal bubble. J. Fluid Mech. 572, 311–337.Google Scholar
Mei, R., Klausner, J. F. & Lawrence, C. J. 1994 A note on the history force on a spherical bubble at finite Reynolds number. Phys. Fluids 6, 418–420.Google Scholar
Mercier, J., Lyrio, A. & Forslund, R. 1997 Three-dimensional study of the nonrectlinear trajectory of air bubbles rising in water. Trans. ASME J. Fluids Engng 119, 233–247.Google Scholar
Moore, D. W. 1965 The velocity of rise of distorted gas bubbles in a liquid of small viscosity. J. Fluid Mech. 23, 749–766.Google Scholar
Mougin, G. & Magnaudet, J. 2001 Path instability of a rising bubble. Phys. Rev. Lett. 88 (1), 014502.Google Scholar
Mougin, G. & Magnaudet, J. 2002 The generalized kirchhoff equations and their application to the interaction between a rigid body and an arbitrary time-dependent viscous flow. Intl J. Multiphase Flow 28 (11), 1837–1851.Google Scholar
Mougin, G. & Magnaudet, J. 2006 Wake-induced forces and torques on a zigzagging/spiralling bubble. J. Fluid Mech. 567, 185–194.Google Scholar
Posner, A. M., Anderson, J. R. & Alexander, A. E. 1952 The surface tension and surface potential of aqueous solutions of normal aliphatic alcohols. J. Colloid Sci. 7 (6), 623–644.Google Scholar
Prosperetti, A. 2004 Bubbles. Phys. Fluids 16, 1852–1865.CrossRefGoogle Scholar
Prosperetti, A., Ohl, C. D., Tijink, A., Mougin, G. & Magnaudet, J. 2003 The added mass of an expanding bubble. J. Fluid Mech. 482, 286–290.Google Scholar
Sadhal, S. S. & Johnson, R. E. 1983 Stokes flow past bubbles and drops partially coated with thin films. Part 1. Stagnant cap of surfactant film–exact solution. J. Fluid Mech. 126 (1), 237–250.Google Scholar
Saffman, P. G. 1956 On the motion of small spheroidal particles in a viscous liquid. J. Fluid Mech. 1, 540–553.CrossRefGoogle Scholar
Saffman, P. G. 1992 Vortex Dynamics. Cambridge University Press.Google Scholar
Sanada, T., Sugihara, K., Shirota, M. & Watanabe, M. 2008 Motion and drag of a single bubble in super-purified water. Fluid Dyn. Res. 40 (7–8), 534–545.Google Scholar
Savic, P. 1953 Circulation and distortion of liquid drops falling through viscous medium. Tech. Rep. MT-22. Natl Res. Counc. Can. Div. Mech. Engng.Google Scholar
Shew, W. & Pinton, J.-F. 2006 Dynamical model of bubble path instability. Phys. Rev. Lett. 97 (14), 144508.Google Scholar
Shew, W. L., Poncett, S. & Pinton, J.-F. 2006 Force measurements on rising bubbles. J. Fluid Mech. 569, 51–60.Google Scholar
Takagi, S. & Matsumoto, Y. 2011 Surfactant effects on bubble motion and bubbly flows. Annu. Rev. Fluid Mech. 43 (1), 615–636.CrossRefGoogle Scholar
Takagi, S., Uda, T., Watanabe, Y. & Matsumoto, Y. 2003 Behavior of a rising bubble in water with surfactant dissolution (1st report, steady behaviour) (in japanese). Trans. JSME, Series B 69, 2192–2199.Google Scholar
Takemura, F. & Yabe, A. 1999 Rising speed and dissolution rate of a carbon dioxide bubble in slightly contaminated water. J. Fluid Mech. 378, 319–334.Google Scholar
Tomiyama, A., Celata, G. P., Hosokawa, S. & Yoshida, S. 2002 Terminal velocity of single bubbles in surface tension force dominant regime. Intl J. Multiphase Flow 28 (9), 1497–1519.Google Scholar
Tsuge, H. & Hibino, S. 1971 The motion of single bubble gas bubbles in various liquids. In Kagaku-kogaku, pp. 65–71.Google Scholar
Veldhuis, C., Biesheuvel, A. & van Wijngaarden, L. 2008 Shape oscillations on bubbles rising in clean and in tap water. Phys. Fluids 20 (4), 040705.Google Scholar
de Vries, A. W. G., Biesheuvel, A. & van Wijngaarden, L. 2002 Notes on the path and wake of a gas bubble rising in pure water. Intl J. Multiphase Flow 28 (11), 1823–1835.Google Scholar
Wang, Y., Papageorgiou, D. T. & Maldarelli, C. 2002 Using surfactants to control the formation and size of wakes behind moving bubbles at order-one Reynolds numbers. J. Fluid Mech. 453, 1–19.CrossRefGoogle Scholar
Wu, M. & Gharib, M. 2002 Experimental studies on the shape and path of small air bubbles rising in clean water. Phys. Fluids 14, L49.Google Scholar
Yang, B. & Prosperetti, A. 2007 Linear stability of the flow past a spheroidal bubble. J. Fluid Mech. 582, 53–78.Google Scholar
Zenit, R. & Magnaudet, J. 2008 Path instability of rising spheroidal air bubbles: A shape-controlled process. Phys. Fluids 20 (6), 061702.Google Scholar
Zenit, R. & Magnaudet, J. 2009 Measurements of the streamwise vorticity in the wake of an oscillating bubble. Intl J. Multiphase Flow 35 (2), 195–203.Google Scholar
Zhang, Y. & Finch, J. A. 2001 A note on single bubble motion in surfactant solutions. J. Fluid Mech. 429, 63–66.Google Scholar