Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-12-01T00:10:32.523Z Has data issue: false hasContentIssue false
  • English
  • Français

Surfactant- and gravity-dependent instability of two-layer channel flows: linear theory covering all wavelengths. Part 2. Mid-wave regimes

Published online by Cambridge University Press:  23 January 2019

Alexander L. Frenkel ,
David Halpern Open the ORCID record for David Halpern [Opens in a new window]  and
Adam J. Schweiger
Alexander L. Frenkel
Affiliation:
Department of Mathematics, University of Alabama, Tuscaloosa, AL 35487, USA
David Halpern*
Affiliation:
Department of Mathematics, University of Alabama, Tuscaloosa, AL 35487, USA
Adam J. Schweiger
Affiliation:
Department of Mathematics, University of Alabama, Tuscaloosa, AL 35487, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The joint effects of an insoluble surfactant and gravity on the linear stability of a two-layer Couette flow in a horizontal channel are investigated. The inertialess instability regimes are studied for arbitrary wavelengths and with no simplifying requirements on the system parameters: the ratio of thicknesses of the two fluid layers; the viscosity ratio; the base shear rate; the Marangoni number 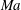$Ma$; and the Bond number 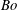$Bo$. As was established in the first part of this investigation (Frenkel, Halpern & Schweiger, J. Fluid Mech., vol. 863, 2019, pp. 150–184), a quadratic dispersion equation for the complex growth rate yields two, largely continuous, branches of the normal modes, which are responsible for the flow stability properties. This is consistent with the surfactant instability case of zero gravity studied in Halpern & Frenkel (J. Fluid Mech., vol. 485, 2003, pp. 191–220). The present paper focuses on the mid-wave regimes of instability, defined as those having a finite interval of unstable wavenumbers bounded away from zero. In particular, the location of the mid-wave instability regions in the (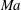$Ma$, 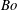$Bo$)-plane, bounded by their critical curves, depending on the other system parameters, is considered. The changes of the extremal points of these critical curves with the variation of external parameters are investigated, including the bifurcation points at which new extrema emerge. Also, it is found that for the less unstable branch of normal modes, a mid-wave interval of unstable wavenumbers may sometimes coexist with a long-wave one, defined as an interval having a zero-wavenumber endpoint.

JFM classification

Instability: Instability Low-Reynolds-number flows: Low-Reynolds-number flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 863 , 25 March 2019 , pp. 185 - 214
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bassom, A. P., Blyth, M. G. & Papageorgiou, D. T. 2010 Nonlinear development of two-layer Couette–Poiseuille flow in the presence of surfactant. Phys. Fluids 22 (10), 102102.10.1063/1.3488226Google Scholar
Blyth, M. G. & Pozrikidis, C. 2004a Effect of inertia on the Marangoni instability of two-layer channel flow. Part II: normal-mode analysis. J. Engng Maths 50 (2–3), 329–341.10.1007/s10665-004-3691-zGoogle Scholar
Blyth, M. G. & Pozrikidis, C. 2004b Effect of surfactants on the stability of two-layer channel flow. J. Fluid Mech. 505, 59–86.10.1017/S0022112003007821Google Scholar
Cross, M. C. & Hohenberg, P. C. 1993 Pattern formation outside of equilibrium. Rev. Mod. Phys. 65, 851–1112.10.1103/RevModPhys.65.851Google Scholar
Edwards, D. A., Brenner, H. & Wasan, D. T. 1991 Interfacial Transport Processes and Rheology. Butterworth-Heinemann.Google Scholar
Frenkel, A. L. & Halpern, D. 2002 Stokes-flow instability due to interfacial surfactant. Phys. Fluids 14 (7), L45–L48.10.1063/1.1483838Google Scholar
Frenkel, A. L. & Halpern, D. 2006 Strongly nonlinear nature of interfacial-surfactant instability of Couette flow. Intl J. Pure Appl. Maths 29 (2), 205–224.Google Scholar
Frenkel, A. L. & Halpern, D. 2017 Surfactant and gravity dependent instability of two-layer Couette flows and its nonlinear saturation. J. Fluid Mech. 826, 158–204.10.1017/jfm.2017.423Google Scholar
Frenkel, A. L., Halpern, D. & Schweiger, A. J.2018 Surfactant and gravity dependent instability of two-layer channel flows: linear theory covering all wave lengths, arXiv:1801.09290.Google Scholar
Frenkel, A. L., Halpern, D. & Schweiger, A. J. 2019 Surfactant- and gravity- dependent instability of two-layer channel flows: linear theory covering all wavelengths. Part 1. ‘Long-wave’ regimes. J. Fluid Mech. 863, 150–184.10.1017/jfm.2018.990Google Scholar
Halpern, D. & Frenkel, A. L. 2003 Destabilization of a creeping flow by interfacial surfactant: linear theory extended to all wavenumbers. J. Fluid Mech. 485, 191–220.10.1017/S0022112003004476Google Scholar
Kalogirou, A. 2018 Instability of two-layer film flows due to the interacting effects of surfactants, inertia, and gravity. Phys. Fluids 30 (3), 030707.Google Scholar
Kalogirou, A. & Papageorgiou, D. T. 2016 Nonlinear dynamics of surfactant-laden two-fluid Couette flows in the presence of inertia. J. Fluid Mech. 802, 5–36.10.1017/jfm.2016.429Google Scholar
Kalogirou, A., Papageorgiou, D. T. & Smyrlis, Y.-S. 2012 Surfactant destabilization and non-linear phenomena in two-fluid shear flows at small Reynolds numbers. IMA J. Appl. Maths 77 (3), 351–360.10.1093/imamat/hxs035Google Scholar
Picardo, J. R., Radhakrishna, T. G. & Pushpavanam, S. 2016 Solutal Marangoni instability in layered two-phase flows. J. Fluid Mech. 793, 280–315.10.1017/jfm.2016.135Google Scholar
Pozrikidis, C. 2004 Effect of inertia on the Marangoni instability of two-layer channel flow, Part I: numerical simulations. J. Engng Maths 50 (2–3), 311–327.10.1007/s10665-004-3690-0Google Scholar
Pozrikidis, C. & Hill, A. I. 2011 Surfactant-induced instability of a sheared liquid layer. IMA J. Appl. Maths 76 (6), 859–875.10.1093/imamat/hxq067Google Scholar
Wei, H. H. 2005 On the flow-induced Marangoni instability due to the presence of surfactant. J. Fluid Mech. 544, 173–200.10.1017/S0022112005006609Google Scholar