Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-24T19:49:33.871Z Has data issue: false hasContentIssue false
  • English
  • Français

Surface wave effects on submesoscale fronts and filaments

Published online by Cambridge University Press:  22 March 2018

James C. McWilliams Open the ORCID record for James C. McWilliams [Opens in a new window]
Get access Rights & Permissions [Opens in a new window]

Abstract

A diagnostic analysis is made for the ageostrophic secondary circulation, buoyancy flux and frontogenetic tendency (SCFT) in upper-ocean submesoscale fronts and dense filaments under the combined influences of boundary-layer turbulent mixing, surface wind stress and surface gravity waves. The analysis is based on a momentum-balance approximation that neglects ageostrophic acceleration, and the surface wave effects are represented with a wave-averaged asymptotic theory based on the time scale separation between wave and current evolution. 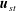The wave’s Stokes-drift velocity $\boldsymbol{u}_{st}$ induces SCFT effects that are dominant in strong swell with weak turbulent mixing, and they combine with Ekman and turbulent thermal wind influences in more general situations near wind–wave equilibrium. The complementary effect of the submesoscale currents on the waves is weak for longer waves near the wind–wave or swell spectrum peak, but it is strong for shorter waves.

JFM classification

Geophysical and Geological Flows: Ocean processes Waves/Free-surface Flows: Surface gravity waves Mixing: Turbulent mixing
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 843 , 25 May 2018 , pp. 479 - 517
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ardhuin, F., Gille, S., Menemenlis, D., Rocha, C. B., Rascle, N., Chapron, B., Gula, J. & Molemaker, M. J. 2017 Small-scale open-ocean currents have large effects on wind-wave heights. J. Geophys. Res. Oceans 122, 4500–4517.Google Scholar
Barkan, R., McWilliams, J. C., Srinivasan, K., Molemaker, M. J. & D’Asaro, E. A. 2017 The dynamical role of horizontal divergence in submesoscale frontogenesis. Geophys. Res. Lett. (submitted).Google Scholar
Belcher, S. E., Grant, A. A. L. M., Hanley, K. E., Fox-Kemper, B., Van Roekel, L., Sullivan, P. P., Large, W. G., Brown, A., Hines, A., Calvert, D. et al. 2012 A global perspective on Langmuir turbulence in the ocean surface boundary layer. Geophys. Res. Lett. 39, L18605.Google Scholar
Bühler, O. 2009 Waves and Mean Flows. Cambridge University Press.Google Scholar
Craik, A. D. D. & Leibovich, S. 1976 A rational model for Langmuir circulations. J. Fluid Mech. 73, 401–426.Google Scholar
Dysthe, K. B. 2001 Refraction of gravity waves by weak current gradients. J. Fluid Mech. 442, 157–159.Google Scholar
Harcourt, R. R. 2013 A second-moment closure model for Langmuir turbulence. J. Phys. Oceanogr. 43, 673–697.Google Scholar
Harcourt, R. R. 2015 An improved second-moment closure model of Langmuir turbulence. J. Phys. Oceanogr. 45, 84–103.Google Scholar
Holm, D. D. 1996 The ideal Craik–Leibovich equations. Physica D 98, 415–441.Google Scholar
Hoskins, B. J. 1982 The mathematical theory of frontogenesis. Annu. Rev. Fluid Mech. 14, 131–151.Google Scholar
Huang, N. E. 1979 On surface drift currents in the ocean. J. Fluid Mech. 91, 119–208.Google Scholar
Kenyon, K. E. 1969 Stokes drift for random gravity waves. J. Geophys. Res. 74, 6991–6994.Google Scholar
Kenyon, K. E. 1971 Wave refraction in ocean currents. Deep-Sea Res. 18, 1023–1034.Google Scholar
Large, W. G., McWilliams, J. C. & Doney, S. C. 1994 Oceanic vertical mixing: a review and a model with a nonlocal boundary layer parameterization. Rev. Geophys. 32, 363–403.Google Scholar
Li, Q. & Fox-Kemper, B. 2017 Assessing the effects of Langmuir turbulence on the entrainment buoyancy flux in the ocean surface boundary layer. J. Phys. Oceanogr. 47, 2863–2886.Google Scholar
McWilliams, J. C. 2016 Submesoscale currents in the ocean. Proc. R. Soc. Lond. A 472, 20160117/1–32.Google Scholar
McWilliams, J. C. 2017 Submesoscale surface fronts and filaments: secondary circulation, buoyancy flux, and frontogenesis. J. Fluid Mech. 823, 391–432.Google Scholar
McWilliams, J. C. & Fox-Kemper, B. 2013 Oceanic wave-balanced surface fronts and filaments. J. Fluid Mech. 730, 464–490.Google Scholar
McWilliams, J. C., Gula, J., Molemaker, M. J., Renault, L. & Shchepetkin, A. F. 2015 Filament frontogenesis by boundary layer turbulence. J. Phys. Oceanogr. 45, 1988–2005.Google Scholar
McWilliams, J. C., Huckle, E., Liang, J.-H. & Sullivan, P. P. 2012 The wavy Ekman layer: Langmuir circulations, breaking waves, and Reynolds stress. J. Phys. Oceanogr. 42, 1793–1816.Google Scholar
McWilliams, J. C., Huckle, E., Liang, J.-H. & Sullivan, P. P. 2014 Langmuir turbulence in swell. J. Phys. Oceanogr. 44, 870–890.Google Scholar
McWilliams, J. C., Restrepo, J. M. & Lane, E. M. 2004 An asymptotic theory for the interaction of waves and currents in coastal waters. J. Fluid Mech. 511, 135–178.Google Scholar
McWilliams, J. C. & Sullivan, P. P. 2000 Vertical mixing by Langmuir circulations. Spill Sci. Technol. Bull. 6, 225–237.Google Scholar
McWilliams, J. C., Sullivan, P. P. & Moeng, C.-H. 1997 Langmuir turbulence in the ocean. J. Fluid Mech. 334, 1–30.Google Scholar
Phillips, O. M. 1984 On the response of short ocean wave components at a fixed wavenumber to ocean current variations. J. Phys. Oceanogr. 14, 1425–1433.Google Scholar
Polton, J. A., Lewis, D. M. & Belcher, S. E. 2005 The role of wave-induced Coriolis–Stokes forcing on the wind-driven mixed layer. J. Phys. Oceanogr. 35, 444–457.Google Scholar
Reichl, B. G., Wang, D., Hara, T., Ginis, I. & Kukulka, T. 2016 Langmuir turbulence parameterization in tropical cyclone conditions. J. Phys. Oceanogr. 46, 863–886.Google Scholar
Romero, L. E., Lemnain, L. & Melville, W. K. 2017 Observations of surface wave-current interaction. J. Phys. Oceanogr. 47, 615–631.Google Scholar
Smyth, W. D., Skyllingstad, E. D., Crawford, G. B. & Wijesekera, H. 2002 Nonlocal fluxes and Stokes drift effects in the K-profile parameterization. Ocean Dyn. 52, 104–115.Google Scholar
Sullivan, P. P. & McWilliams, J. C. 2010 Dynamics of winds and currents coupled to surface waves. Annu. Rev. Fluid Mech. 42, 19–42.Google Scholar
Suzuki, N. & Fox-Kemper, B. 2016 Understanding Stokes forces in the wave-averaged equations. J. Geophys. Res. Oceans 121, 3579–3596.Google Scholar
Van Roekel, L. P., Fox-Kemper, B., Sullivan, P. P., Hamlington, P. E. & Haney, S. R. 2012 The form and orientation of Langmuir cells for misaligned winds and waves. J. Geophys. Res. Oceans 117, C05001.Google Scholar
Webb, A. & Fox-Kemper, B. 2011 Wave spectral moments and Stokes drift estimation. Ocean Model. 40, 273–288.Google Scholar
Wenegrat, J. O. & McPhadden, M. J. 2016 Wind, waves, and fronts: frictional effects in a generalized Ekman model. J. Phys. Oceanogr. 46, 711–747.Google Scholar