Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T16:57:11.682Z Has data issue: false hasContentIssue false
  • English
  • Français

Surface manifestation of internal waves emitted by submerged localized stratified turbulence

Published online by Cambridge University Press:  06 June 2016

Qi Zhou  and
Peter J. Diamessis
Qi Zhou
Affiliation:
School of Civil and Environmental Engineering, Cornell University, Ithaca, NY 14853, USA
Peter J. Diamessis
Affiliation:
School of Civil and Environmental Engineering, Cornell University, Ithaca, NY 14853, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

The internal waves (IWs) radiated by the turbulent wake of a sphere of diameter 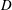$D$ towed at speed 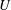$U$ are investigated using three-dimensional fully nonlinear simulations performed in a linearly stratified Boussinesq fluid with buoyancy frequency 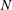$N$. The study focuses on a broad range of wave characteristics in the far field of the turbulent wave source, specifically at the sea surface (as modelled by a free-slip rigid lid) where the IWs reflect. Six simulations are performed at Reynolds number 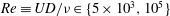$Re\equiv UD/{\it\nu}\in \{5\times 10^{3},10^{5}\}$ and Froude number 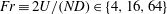$Fr\equiv 2U/(ND)\in \{4,16,64\}$, where ${\it\nu}$ is viscosity. The wave-emitting wake is located at a fixed distance of 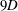$9D$ below the surface. As the wake evolves for up to 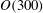$O(300)$ units of buoyancy time scale 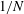$1/N$, IW characteristics, such as horizontal wavelength 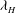${\it\lambda}_{H}$ and wave period 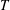$T$, are sampled at the sea surface via wavelet transforms of horizontal divergence signals. The statistics of amplitudes and orientations of IW-induced surface strains are also reported. The mean dimensionless observable wavelength 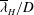$\overline{{\it\lambda}}_{H}/D$ at the sea surface decays in time as 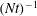$(Nt)^{-1}$, which is due to the waves’ dispersion. This observation is in agreement with a linear propagation model that is independent of the wake 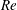$Re$ and 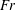$Fr$. This agreement further suggests that the most energetic waves impacting the surface originate from the early-time wake that is adjusting to buoyancy. The most energetic dimensionless wavelength 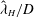$\hat{{\it\lambda}}_{H}/D$ is found to scale as 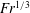$Fr^{1/3}$ and decrease with 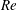$Re$, which causes the arrival time (in 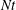$Nt$ units) of the strongest waves at the surface to scale as 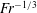$Fr^{-1/3}$ and increase with 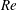$Re$. This wavelength 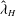$\hat{{\it\lambda}}_{H}$ is also found to correlate with the vertical Taylor scale of the wake turbulence. IW-driven phenomena at the surface that are of interest to an observer, such as the local enrichment of surfactant and the transport of ocean surface tracers, are also examined. The local enrichment ratio of surface scalar scales linearly with the steepness of IWs that reach the surface, and the ratio often exceeds a possible visibility threshold. The Lagrangian drifts of ocean tracers, which are linked to the nonlinear interaction between incident and reflecting IW packets, create a local divergence in lateral mass transport right above the wake centreline, an effect that intensifies strongly with increasing 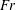$Fr$. The findings of this study may serve as a platform to investigate the generation and surface manifestation of IWs radiated by other canonical submerged stratified turbulent flows.

JFM classification

Geophysical and Geological Flows: Internal waves Turbulent Flows: Stratified turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 798 , 10 July 2016 , pp. 505 - 539
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdilghanie, A. M.2010 A numerical investigation of turbulence-driven and forced generation of internal gravity waves in stratified mid-water. PhD thesis, Cornell University, Ithaca, New York.Google Scholar
Abdilghanie, A. M. & Diamessis, P. J. 2013 The internal gravity wave field emitted by a stably stratified turbulent wake. J. Fluid Mech. 720, 104–139; referred to in text as ‘A&D’.Google Scholar
Akylas, T. R., Grimshaw, R. H. J., Clarke, S. R. & Tabaei, A. 2007 Reflecting tidal wave beams and local generation of solitary waves in the ocean thermocline. J. Fluid Mech. 593, 297–313.Google Scholar
Alpers, W. 1985 Theory of radar imaging of internal waves. Nature 314, 245–247.CrossRefGoogle Scholar
Billant, P. & Chomaz, J.-M. 2001 Self-similarity of strongly stratified inviscid flows. Phys. Fluids 13, 1645.Google Scholar
Bonneton, P., Chomaz, J.-M. & Hopfinger, E. J. 1993 Internal waves produced by the turbulent wake of a sphere moving horizontally in a stratified fluid. J. Fluid Mech. 254, 23–40.CrossRefGoogle Scholar
Brandt, A. & Rottier, J. R. 2015 The internal wavefield generated by a towed sphere at low Froude number. J. Fluid Mech. 769, 103–129.Google Scholar
Brethouwer, G., Billant, P., Lindborg, E. & Chomaz, J.-M. 2007 Scaling analysis and simulation of strongly stratified turbulent flows. J. Fluid Mech. 585, 343–368.Google Scholar
Brucker, K. A. & Sarkar, S. 2010 A comparative study of self-propelled and towed wakes in a stratified fluid. J. Fluid Mech. 652, 373–404.Google Scholar
Dairay, T., Obligado, M. & Vassilicos, J. C. 2015 Non-equilibrium scaling laws in axisymmetric turbulent wakes. J. Fluid Mech. 781, 166–195.Google Scholar
Dallard, T. & Spedding, G. R. 1993 2-D wavelet transforms: generalisation of the Hardy space and application to experimental studies. Eur. J. Mech. (B/Fluids) 12, 107–134.Google Scholar
Davidson, P. A. 2013 Turbulence in Rotating, Stratified and Electrically Conducting Fluids. Cambridge University Press.Google Scholar
Devore, J. 2015 Probability and Statistics for Engineering and the Sciences. Cengage Learning.Google Scholar
Diamessis, P. J., Domaradzki, J. A. & Hesthaven, J. S. 2005 A spectral multidomain penalty method model for the simulation of high Reynolds number localized incompressible stratified turbulence. J. Comput. Phys. 202, 298–322.Google Scholar
Diamessis, P. J., Spedding, G. R. & Domaradzki, J. A. 2011 Similarity scaling and vorticity structure in high-Reynolds-number stably stratified turbulent wakes. J. Fluid Mech. 671, 52–95; referred to in text as ‘DSD’.Google Scholar
Diamessis, P. J., Wunsch, S., Delwiche, I. & Richter, M. P. 2014 Nonlinear generation of harmonics through the interaction of an internal wave beam with a model oceanic pycnocline. Dyn. Atmos. Oceans 66, 110–137.Google Scholar
Dommermuth, D. G., Rottman, J. W., Innis, G. E. & Novikov, E. A. 2002 Numerical simulation of the wake of a towed sphere in a weakly stratified fluid. J. Fluid Mech. 473, 83–101.Google Scholar
Druzhinin, O. A. 2009 Generation of internal waves by a turbulent jet in a stratified fluid. Fluid Dyn. 44, 213–223.CrossRefGoogle Scholar
Dupont, P., Kadri, Y. & Chomaz, J.-M. 2001 Internal waves generated by the wake of Gaussian hills. Phys. Fluids 13, 3223–3233.CrossRefGoogle Scholar
Dupont, P. & Voisin, B. 1996 Internal waves generated by a translating and oscillating sphere. Dyn. Atmos. Oceans 23, 289–298.Google Scholar
Ermakov, S. A., Salashin, S. G. & Panchenko, A. R. 1992 Film slicks on the sea surface and some mechanisms of their formation. Dyn. Atmos. Oceans 16, 279–304.Google Scholar
Ewing, G. C. 1950a Relation between band slicks at the surface and internal waves in the sea. Science 111, 91–94.Google Scholar
Ewing, G. C. 1950b Slicks, surface films and internal waves. J. Mar. Res. 9, 161–187.Google Scholar
Fung, Y. T. & Chang, S. W. 1996 Surface and internal signatures of organized vortex motions in stratified fluids. Phys. Fluids 8, 3023–3056.Google Scholar
Gibson, C. H. 1980 Fossil temperature, salinity and vorticity in the ocean. In Marine Turbulence (ed. Nihoul, J. C. T.), pp. 221–258. Elsevier.Google Scholar
Gilreath, H. E. & Brandt, A. 1985 Experiments on the generation of internal waves in a stratified fluid. AIAA J. 23, 693–700.Google Scholar
Gourlay, M. J., Arendt, S. C., Fritts, D. C. & Werne, J. 2001 Numerical modeling of initially turbulent wakes with net momentum. Phys. Fluids 13, 3783–3802.Google Scholar
Grisouard, N., Staquet, C. & Gerkema, T. 2011 Generation of internal solitary waves in a pycnocline by an internal wave beam: a numerical study. J. Fluid Mech. 676, 491–513.Google Scholar
Hebert, D. A. & de Bruyn Kops, S. M. 2006 Predicting turbulence in flows with strong stable stratification. Phys. Fluids 18, 066602.Google Scholar
Hopfinger, E. J., Flor, J.-B., Chomaz, J.-M. & Bonneton, P. 1991 Internal waves generated by a moving sphere and its wake in a stratified fluid. Exp. Fluids 11, 255–261.Google Scholar
Hwung, H.-H., Yang, R.-Y. & Shugan, I. V. 2009 Exposure of internal waves on the sea surface. J. Fluid Mech. 626, 1–20.Google Scholar
Källén, E. 1987 Surface effects of vertically propagating gravity waves in a stratified fluid. J. Fluid Mech. 182, 111–125.Google Scholar
Keeler, R. N., Bondur, V. G. & Gibson, C. H. 2005 Optical satellite imagery detection of internal wave effects from a submerged turbulent outfall in the stratified ocean. Geophys. Res. Lett. 32, L12610.Google Scholar
Klemas, V. 2012 Remote sensing of ocean internal waves: an overview. J. Coast. Res. 28, 540–546.CrossRefGoogle Scholar
Lamb, K. G. 2004 Nonlinear interaction among internal wave beams generated by tidal flow over supercritical topography. Geophys. Res. Lett. 31, L09313.Google Scholar
Lighthill, J. 1978 Waves in Fluids. Cambridge University Press.Google Scholar
Lin, J.-T. & Pao, Y.-H. 1979 Wakes in stratified fluids. Annu. Rev. Fluid Mech. 11, 317–338.Google Scholar
Lin, Q., Boyer, D. L. & Fernando, H. J. S. 1993 Internal waves generated by the turbulent wake of a sphere. Exp. Fluids 15, 147–154.Google Scholar
Maffioli, A., Davidson, P. A., Dalziel, S. B. & Swaminathan, N. 2014 The evolution of a stratified turbulent cloud. J. Fluid Mech. 739, 229–253.Google Scholar
Mathur, M. & Peacock, T. 2009 Internal wave beam propagation in non-uniform stratifications. J. Fluid Mech. 639, 133–152.Google Scholar
Mercier, M. J., Mathur, M., Gostiaux, L., Gerkema, T., Magalhaes, J. M., da Silva, J. C. B. & Dauxois, T. 2012 Soliton generation by internal tidal beams impinging on a pycnocline: laboratory experiments. J. Fluid Mech. 704, 37–60.Google Scholar
Meunier, P. 2012 Stratified wake of a tilted cylinder. Part 2. Lee internal waves. J. Fluid Mech. 699, 198–215.Google Scholar
Meunier, P., Diamessis, P. J. & Spedding, G. R. 2006 Self-preservation in stratified momentum wakes. Phys. Fluids 18, 106601.Google Scholar
Moum, J. N., Carlson, D. J. & Cowles, T. J. 1990 Sea slicks and surface strain. Deep-Sea Res. 37, 767–775.Google Scholar
Moum, J. N. & Smyth, W. D. 2006 The pressure disturbance of a nonlinear internal wave train. J. Fluid Mech. 558, 153–177.CrossRefGoogle Scholar
Mowbray, D. E. & Rarity, B. S. H. 1967 A theoretical and experimental investigation of the phase configuration of internal waves of small amplitude in a density stratified liquid. J. Fluid Mech. 28, 1–16.Google Scholar
Orr, T. S., Domaradzki, J. A., Spedding, G. R. & Constantinescu, G. S. 2015 Numerical simulations of the near wake of a sphere moving in a steady, horizontal motion through a linearly stratified fluid at Re = 1000. Phys. Fluids 27, 035113.Google Scholar
Orszag, S. A. & Pao, Y. H. 1975 Numerical computation of turbulent shear flows. Adv. Geophys. 18, 225–236.Google Scholar
Osborne, M. F. M. 1964 The interpretation of infrared radiation from the sea in terms of its boundary layer. Dtsch. Hydrogr. Z. 17, 115–136.Google Scholar
Osborne, M. F. M. 1965 The effect of convergent and divergent flow patterns on infrared and optical radiation from the sea. Dtsch. Hydrogr. Z. 18, 1–25.CrossRefGoogle Scholar
Pal, A., de Stadler, M. B. & Sarkar, S. 2013 The spatial evolution of fluctuations in a self-propelled wake compared to a patch of turbulence. Phys. Fluids 25, 095106.Google Scholar
Pasquetti, R. 2011 Temporal/spatial simulation of the stratified far wake of a sphere. Comput. Fluids 40, 179–187.Google Scholar
Press, W. H., Teukolsky, S. A., Vetterling, W. T. & Flannery, B. P. 2007 Numerical Recipes: The Art of Scientific Computing, 3rd edn. Cambridge University Press.Google Scholar
Redford, J. A., Lund, T. S. & Coleman, G. N. 2015 A numerical study of a weakly stratified turbulent wake. J. Fluid Mech. 776, 568–609.CrossRefGoogle Scholar
Riley, J. J. & de Bruyn Kops, S. M. 2003 Dynamics of turbulence strongly influenced by buoyancy. Phys. Fluids 15, 2047.Google Scholar
Riley, J. J. & Lindborg, E. 2012 Recent progress in stratified turbulence. In Ten Chapters in Turbulence (ed. Davidson, P. A., Kaneda, Y. & Sreenivasan, K. R.), pp. 269–317. Cambridge University Press.Google Scholar
Robey, H. F. 1997 The generation of internal waves by a towed sphere and its wake in a thermocline. Phys. Fluids 9, 3353–3367.Google Scholar
Soloviev, A. & Lukas, R. 2006 The Near-Surface Layer of the Ocean. Springer.Google Scholar
Spedding, G. R. 1997 The evolution of initially turbulent bluff-body wakes at high internal Froude number. J. Fluid Mech. 337, 283–301.Google Scholar
Spedding, G. R. 2002 Vertical structure in stratified wakes with high initial Froude number. J. Fluid Mech. 454, 71–112.Google Scholar
Spedding, G. R. 2014 Wake signature detection. Annu. Rev. Fluid Mech. 46, 273–302.Google Scholar
Spedding, G. R., Browand, F. K., Bell, R. & Chen, J. 2000 Internal waves from intermediate, or late-wake vortices. In Stratified Flows I, Proceedings of the 5th International Symposium on Stratified Flows, pp. 113–118. University of British Columbia.Google Scholar
Spedding, G. R., Browand, F. K. & Fincham, A. M. 1996 Turbulence, similarity scaling and vortex geometry in the wake of a towed sphere in a stably stratified fluids. J. Fluid Mech. 314, 53–103.Google Scholar
Spedding, G. R., Browand, F. K., Huang, N. & Long, S. R. 1993 A 2-D complex wavelet analysis of an unsteady wind-generated surface-wave field. Dyn. Atmos. Oceans 20, 55–77.Google Scholar
Stevenson, T. N. 1973 The phase configuration of internal waves around a body moving in a density stratified fluid. J. Fluid Mech. 60, 759–767.CrossRefGoogle Scholar
Sutherland, B. R. 2010 Internal Gravity Waves. Cambridge University Press.Google Scholar
Sutherland, B. R. & Linden, P. F. 1998 Internal wave excitation from stratified flow over a thin barrier. J. Fluid Mech. 377, 223–252.Google Scholar
Tabaei, A. & Akylas, T. R. 2003 Nonlinear internal gravity wave beams. J. Fluid Mech. 482, 141–161.Google Scholar
Tabaei, A., Akylas, T. R. & Lamb, K. G. 2005 Nonlinear effects in reflecting and colliding internal wave beams. J. Fluid Mech. 526, 217–243.Google Scholar
Taylor, J. R. & Sarkar, S. 2007 Internal gravity waves generated by a turbulent bottom Ekman layer. J. Fluid Mech. 590, 331–354.Google Scholar
Thorpe, S. A. 1975 The excitation, dissipation, and interaction of internal waves in the deep ocean. J. Geophys. Res. 80, 328–338.Google Scholar
Thorpe, S. A. 2005 The Turbulent Ocean. Cambridge University Press.Google Scholar
Voisin, B. 1995 Internal wave generation by turbulent wakes. In Mixing in Geophysical Flows (ed. Redondo, J. M. & Métais, O.), pp. 291–301. CIMNE.Google Scholar
Voropayev, S. I., Fernando, H. J. S. & Nath, C. 2009 Thermal and dynamic surface signatures of the wake of a submerged sphere. J. Vis. 12, 285.Google Scholar
Voropayev, S. I., Fernando, H. J. S., Smirnov, S. A. & Morrison, R. 2007 On surface signatures generated by submerged momentum sources. Phys. Fluids 19, 076603.Google Scholar
Winters, K. B. & D’Asaro, E. A. 1989 Two-dimensional instability of finite amplitude internal gravity wave packets near a critical level. J. Geophys. Res. 94, 12709–12719.Google Scholar
Wunsch, S., Ku, H., Delwiche, I. & Awadallah, R. 2014 Simulations of nonlinear harmonic generation by an internal wave beam incident on a pycnocline. Nonlinear Process. Geophy. 21, 855–868.Google Scholar
Zappa, C. J. & Jessup, A. T. 2005 High resolution airborne infrared measurements of ocean skin temperature. IEEE Trans. Geosci. Remote Sens. 2, 146–150.Google Scholar
Zhou, Q.2015 Far-field evolution of turbulence-emitted internal waves and Reynolds number effects on a localized stratified turbulent flow. PhD thesis, Cornell University, Ithaca, New York.Google Scholar
Zhou, Q. & Diamessis, P. J. 2013 Reflection of an internal gravity wave beam off a horizontal free-slip surface. Phys. Fluids 25, 036601.Google Scholar
Zhou, Q. & Diamessis, P. J. 2015 Lagrangian flows within reflecting internal waves at a horizontal free-slip surface. Phys. Fluids 27, 126601.Google Scholar