Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Leong, Thomas
Yasui, Kyuichi
Kato, Kazumi
Harvie, Dalton
Ashokkumar, Muthupandian
and
Kentish, Sandra
2014.
Effect of surfactants on single bubble sonoluminescence behavior and bubble surface stability.
Physical Review E,
Vol. 89,
Issue. 4,
Liu, Yunqiao
Sugiyama, Kazuyasu
and
Takagi, Shu
2015.
Effects of the Encapsulating Membranes on the Translations of Pairs of Non-spherical Bubbles.
Journal of Physics: Conference Series,
Vol. 656,
Issue. ,
p.
012026.
Gaudron, R.
Warnez, M. T.
and
Johnsen, E.
2015.
Bubble dynamics in a viscoelastic medium with nonlinear elasticity.
Journal of Fluid Mechanics,
Vol. 766,
Issue. ,
p.
54.
Wang, Qianxi
Manmi, Kawa
and
Calvisi, Michael L.
2015.
Numerical modeling of the 3D dynamics of ultrasound contrast agent microbubbles using the boundary integral method.
Physics of Fluids,
Vol. 27,
Issue. 2,
Xia, Lang
Porter, Tyrone M.
and
Sarkar, Kausik
2015.
Interpreting attenuation at different excitation amplitudes to estimate strain-dependent interfacial rheological properties of lipid-coated monodisperse microbubbles.
The Journal of the Acoustical Society of America,
Vol. 138,
Issue. 6,
p.
3994.
Wang, Qianxi
Manmi, Kawa
and
Liu, Kuo-Kang
2015.
Cell mechanics in biomedical cavitation.
Interface Focus,
Vol. 5,
Issue. 5,
p.
20150018.
Shang, Xiaopeng
Huang, Xiaoyang
and
Yang, Chun
2016.
Bubble dynamics in a microfluidic chamber under low-frequency actuation.
Microfluidics and Nanofluidics,
Vol. 20,
Issue. 1,
Liu, Yunqiao
Sugiyama, Kazuyasu
and
Takagi, Shu
2016.
On the interaction of two encapsulated bubbles in an ultrasound field.
Journal of Fluid Mechanics,
Vol. 804,
Issue. ,
p.
58.
Liu, Yunqiao
and
Wang, Qianxi
2016.
Stability and natural frequency of nonspherical mode of an encapsulated microbubble in a viscous liquid.
Physics of Fluids,
Vol. 28,
Issue. 6,
Poulichet, Vincent
Huerre, Axel
and
Garbin, Valeria
2017.
Shape oscillations of particle-coated bubbles and directional particle expulsion.
Soft Matter,
Vol. 13,
Issue. 1,
p.
125.
Liu, Yunqiao
Calvisi, Michael L
and
Wang, Qianxi
2017.
Nonlinear oscillation and interfacial stability of an encapsulated microbubble under dual-frequency ultrasound.
Fluid Dynamics Research,
Vol. 49,
Issue. 2,
p.
025518.
Liu, Yunqiao
Calvisi, Michael L.
and
Wang, Qianxi
2018.
Shape oscillation and stability of an encapsulated microbubble translating in an acoustic wave.
The Journal of the Acoustical Society of America,
Vol. 144,
Issue. 4,
p.
2189.
Zhang, Yuning
Gao, Yuhang
and
Du, Xiaoze
2018.
Stability mechanisms of oscillating vapor bubbles in acoustic fields.
Ultrasonics Sonochemistry,
Vol. 40,
Issue. ,
p.
808.
Wang, Shi-Ping
Zhang, A-Man
Liu, Yun-Long
Zhang, Shuai
and
Cui, Pu
2018.
Bubble dynamics and its applications.
Journal of Hydrodynamics,
Vol. 30,
Issue. 6,
p.
975.
Liu, Yunqiao
He, Dongdong
Gong, Xiaobo
and
Huang, Huaxiong
2018.
Deformation of an encapsulated bubble in steady and oscillatory electric fields.
Journal of Fluid Mechanics,
Vol. 844,
Issue. ,
p.
567.
Jiménez-Fernández, J.
2018.
Dependence of the subharmonic signal from contrast agent microbubbles on ambient pressure: A theoretical analysis.
The Journal of the Acoustical Society of America,
Vol. 143,
Issue. 1,
p.
169.
Dollet, Benjamin
Marmottant, Philippe
and
Garbin, Valeria
2019.
Bubble Dynamics in Soft and Biological Matter.
Annual Review of Fluid Mechanics,
Vol. 51,
Issue. 1,
p.
331.
Zhang, Zhi
Wang, Aosong
Wu, Jian
Liu, YanZhang
Huang, Dapeng
Qiu, Yan
and
Li, Jilong
2019.
Spatial confinement effects of bubbles produced by laser ablation in liquids.
AIP Advances,
Vol. 9,
Issue. 12,
Murakami, Kazuya
Gaudron, Renaud
and
Johnsen, Eric
2020.
Shape stability of a gas bubble in a soft solid.
Ultrasonics Sonochemistry,
Vol. 67,
Issue. ,
p.
105170.
Cui, Pu
Zhang, A-Man
Wang, Shi-Ping
and
Liu, Yun-Long
2020.
Experimental study on interaction, shock wave emission and ice breaking of two collapsing bubbles.
Journal of Fluid Mechanics,
Vol. 897,
Issue. ,
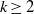 . Two amplitudes for each shape mode are introduced because the membrane moves not only in the radial direction but also in the tangential direction. The system with a boundary layer approximation is reduced to Mathieu’s equation. A simple expression for the natural frequency of the shape mode is derived, which is validated by direct numerical simulation. Stability diagrams for the higher-order shape mode are mapped out in the phase space of driving amplitude and frequency over a range of values of the elastic modulus of the membrane. The most unstable driving frequency is found to satisfy an integer multiple relationship of the form
. Two amplitudes for each shape mode are introduced because the membrane moves not only in the radial direction but also in the tangential direction. The system with a boundary layer approximation is reduced to Mathieu’s equation. A simple expression for the natural frequency of the shape mode is derived, which is validated by direct numerical simulation. Stability diagrams for the higher-order shape mode are mapped out in the phase space of driving amplitude and frequency over a range of values of the elastic modulus of the membrane. The most unstable driving frequency is found to satisfy an integer multiple relationship of the form 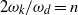 , due to the structure of Mathieu’s equation in the system. In addition to the resonance interaction, liquid viscosity plays an important role in the stability of the encapsulated bubble.
, due to the structure of Mathieu’s equation in the system. In addition to the resonance interaction, liquid viscosity plays an important role in the stability of the encapsulated bubble.