Article contents
Suppression of internal waves by thermohaline staircases
Published online by Cambridge University Press: 07 September 2020
Abstract
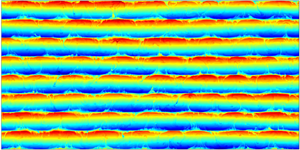
This study attempts to quantify and explain the systematic weakening of internal gravity waves in fingering and diffusive thermohaline staircases. The interaction between waves and staircases is explored using a combination of direct numerical simulations (DNS) and an asymptotic multiscale model. The multiscale theory makes it possible to express the wave decay rate  $({\lambda _d})$ as a function of its wavenumbers and staircase parameters. We find that the decay rates in fully developed staircases greatly exceed values that can be directly attributed to molecular dissipation. They rapidly increase with increasing wavenumbers, both vertical and horizontal. At the same time,
$({\lambda _d})$ as a function of its wavenumbers and staircase parameters. We find that the decay rates in fully developed staircases greatly exceed values that can be directly attributed to molecular dissipation. They rapidly increase with increasing wavenumbers, both vertical and horizontal. At the same time,  ${\lambda _d}$ is only weakly dependent on the thickness of layers in the staircase, the overall density ratio and the diffusivity ratio. The proposed physical mechanism of attenuation emphasizes the significance of eddy diffusion of temperature and salinity, whereas eddy viscosity plays a secondary role in damping internal waves. The asymptotic model is successfully validated by the DNS performed in numerically accessible regimes. We also discuss potential implications of staircase-induced suppression for diapycnal mixing by overturning internal waves in the ocean.
${\lambda _d}$ is only weakly dependent on the thickness of layers in the staircase, the overall density ratio and the diffusivity ratio. The proposed physical mechanism of attenuation emphasizes the significance of eddy diffusion of temperature and salinity, whereas eddy viscosity plays a secondary role in damping internal waves. The asymptotic model is successfully validated by the DNS performed in numerically accessible regimes. We also discuss potential implications of staircase-induced suppression for diapycnal mixing by overturning internal waves in the ocean.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 4
- Cited by



