Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-01-10T07:17:01.189Z Has data issue: false hasContentIssue false
  • English
  • Français

Superhydrophobic annular pipes: a theoretical study

Published online by Cambridge University Press:  13 November 2020

Darren G. Crowdy Open the ORCID record for Darren G. Crowdy [Opens in a new window]
Darren G. Crowdy*
Affiliation:
Department of Mathematics, Imperial College London, 180 Queen's Gate, LondonSW7 2AZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

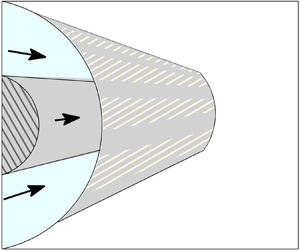
Analytical solutions are presented for longitudinal flow along a superhydrophobic annular pipe where one wall, either the inner or outer, is a fully no-slip boundary while the other is a no-slip wall decorated by a rotationally symmetric pattern of no-shear longitudinal stripes. Formulas are given for the effective slip length associated with laminar flow along the superhydrophobic pipe and the friction properties are characterized. It is shown how these new solutions generalize two solutions to mixed no-slip/no-shear boundary value problems due to Philip (Z. Angew. Math. Phys., vol. 23, 1972, pp. 353–372) for flow in a single-walled superhydrophobic pipe and a superhydrophobic channel. This is done by providing alternative representations of Philip's two solutions, including a useful new formula for the effective slip length for his channel flow solution. For a superhydrophobic annular pipe with inner-wall no-shear patterning there is an optimal pipe bore for enhancing hydrodynamic slip for a given pattern of no-shear stripes. These optimal pipes have a ratio of inner–outer pipe radii in the approximate range 0.5–0.6 and depending only weakly on the geometry of the surface patterning. Boundary point singularities are found to be deleterious to the slip suggesting that, in designing slippery pipes, maximizing the size of uninterrupted no-shear regions is preferable to covering the same surface area with a larger number of smaller no-shear zones. The results add to a list of analytical solutions to mixed boundary value problems relevant to modelling superhydrophobic surfaces.

JFM classification

Flow Control: Drag reduction Biological Fluid Dynamics: Biomedical flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 906 , 10 January 2021 , A15
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Asmolov, E. S. & Vinogradova, O. I. 2012 Effective slip boundary conditions for arbitrary one-dimensional surfaces. J. Fluid Mech. 706, 108–117.CrossRefGoogle Scholar
Crowdy, D. G. 2011 a Frictional slip lengths for unidirectional superhydrophobic grooved surfaces. Phys. Fluids 23, 072001.CrossRefGoogle Scholar
Crowdy, D. G. 2011 b Slip length for longitudinal shear flow over a dilute periodic mattress of protruding bubbles. Phys. Fluids 22, 121703.CrossRefGoogle Scholar
Crowdy, D. G. 2016 Analytical formulae for longitudinal slip lengths over unidirectional superhydrophobic surfaces with curved menisci. J. Fluid Mech. 791, R7.CrossRefGoogle Scholar
Crowdy, D. G. 2017 a Effect of shear thinning on superhydrophobic slip: perturbative corrections to the effective slip length. Phys. Rev. Fluids 2, 124201.CrossRefGoogle Scholar
Crowdy, D. G. 2017 b Effective slip lengths for immobilized superhydrophobic surfaces. J. Fluid Mech. 825, R2.CrossRefGoogle Scholar
Crowdy, D. G. 2017 c Perturbation analysis of subphase gas and meniscus curvature effects for longitudinal flows over superhydrophobic surfaces. J. Fluid Mech. 822, 307–326.CrossRefGoogle Scholar
Crowdy, D. G. 2017 d Slip length for transverse shear flow over a periodic array of weakly curved menisci. Phys. Fluids 29, 091702.CrossRefGoogle Scholar
Crowdy, D. G. 2020 Solving Problems in Multiply Connected Domains. Society for Industrial and Applied Mathematics.CrossRefGoogle Scholar
Escudier, M. P. 2017 Introduction to Engineering Fluid Mechanics. Oxford University Press.Google Scholar
Geraldi, N. R., Dodd, L. E., Xu, B. B., Wells, G. G., Newton, M. I. & McHale, G. 2017 Drag reduction properties of superhydrophobic mesh pipes. Surf. Topogr.: Metrol. Prop. 5, 034001.CrossRefGoogle Scholar
Kirk, T. L., Hodes, M. & Papageorgiou, D. T. 2017 Nusselt numbers for Poiseuille flow over isoflux parallel ridges accounting for meniscus curvature. J. Fluid Mech. 811, 315–349.CrossRefGoogle Scholar
Lee, C., Choi, C.-H. & Kim, C.-J. 2016 Superhydrophobic drag reduction in laminar flows: a critical review. Exp. Fluids 57, 176–196.CrossRefGoogle Scholar
Lv, F. Y. & Zhang, P. 2016 Drag reduction and heat transfer characteristics of water flow through the tubes with superhydrophobic surfaces. Energy Convers. Manage. 113, 165–176.CrossRefGoogle Scholar
Marshall, J. S. 2017 Exact formulae for the effective slip length of a symmetric superhydrophobic channel with flat or weakly curved menisci. SIAM J. Appl. Maths 77, 1606–1630.CrossRefGoogle Scholar
Nizkaya, T. V., Asmolov, E. S. & Vinogradova, O. I. 2014 Gas cushion model and hydrodynamic boundary conditions for superhydrophobic textures. Phys. Rev. E 90, 043017.CrossRefGoogle ScholarPubMed
Philip, J. R. 1972 Flows satisfying mixed no-slip and no-shear conditions. Z. Angew. Math. Phys. 23, 353–372.CrossRefGoogle Scholar
Rothstein, J. P. 2010 Slip on superhydrophobic surfaces. Annu. Rev. Fluid Mech. 109, 42–89.Google Scholar
Sbragaglia, M. & Prosperetti, A. 2007 A note on the effective slip properties for microchannel flows with ultrahydrophobic surfaces. Phys. Fluids 19, 043603.CrossRefGoogle Scholar
Schnitzer, O. 2016 Singular effective slip length for longitudinal flow over a dense bubble mattress. Phys. Rev. Fluids 1, 052101(R).CrossRefGoogle Scholar
Schönecker, C., Baier, T. & Hardt, S. 2014 Influence of the enclosed fluid on the flow over a microstructured surface in the Cassie state. J. Fluid Mech. 740, 168–195.CrossRefGoogle Scholar
Schönecker, C. & Hardt, S. 2013 Longitudinal and transverse flow over a cavity containing a second immiscible fluid. J. Fluid Mech. 717, 376–394.CrossRefGoogle Scholar
Shirtcliffe, N. J., McHale, G., Newton, M. I. & Zhang, Y. 2009 Superhydrophobic copper tubes with possible flow enhancement and drag reduction. ACS Appl. Mater. Inter. 1, 1316–1323.CrossRefGoogle ScholarPubMed
Teo, C. J. & Khoo, B. C. 2009 Analysis of Stokes flow in microchannels with superhydrophobic surfaces containing a periodic array of micro-grooves. Microfluid Nanofluid 7, 352–382.CrossRefGoogle Scholar
Walker, G. M., Albadarin, A. B., McGlue, A., Brennan, S. & Bell, S. E. J. 2014 Analysis of friction factor reduction in turbulent water flow using a superhydrophobic coating. Prog. Org. Coat. 90, 472–476.CrossRefGoogle Scholar
Watanabe, K., Udagawa, Y. & Udagawa, H. 1999 Drag reduction of Newtonian fluid in a circular pipe with a highly water-repellent wall. J. Fluid Mech. 381, 225–238.CrossRefGoogle Scholar
Williams, J. G., Turney, B. W., Moulton, D. E. & Waters, S. L. 2020 Effects of geometry on resistance in elliptical pipe flows. J. Fluid Mech. 891, 1–40.CrossRefGoogle Scholar
Yariv, E. & Crowdy, D. G. 2019 Thermocapillary flow between grooved superhydrophobic surfaces: transverse temperature gradients. J. Fluid Mech. 871, 775–798.CrossRefGoogle Scholar
Yariv, E. & Siegel, M. 2019 Rotation of a superhydrophobic cylinder in a viscous liquid. J. Fluid Mech. 880, R4.CrossRefGoogle Scholar