Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gao, Qiang
Deane, Grant B.
and
Shen, Lian
2021.
Bubble production by air filament and cavity breakup in plunging breaking wave crests.
Journal of Fluid Mechanics,
Vol. 929,
Issue. ,
Farsoiya, Palas Kumar
Popinet, Stéphane
and
Deike, Luc
2021.
Bubble-mediated transfer of dilute gas in turbulence.
Journal of Fluid Mechanics,
Vol. 920,
Issue. ,
Håkansson, Andreas
2021.
The Role of Stochastic Time-Variations in Turbulent Stresses When Predicting Drop Breakup—A Review of Modelling Approaches.
Processes,
Vol. 9,
Issue. 11,
p.
1904.
Perrard, Stéphane
Rivière, Aliénor
Mostert, Wouter
and
Deike, Luc
2021.
Bubble deformation by a turbulent flow.
Journal of Fluid Mechanics,
Vol. 920,
Issue. ,
Håkansson, Andreas
2021.
Towards a Standard Method for Estimating Fragmentation Rates in Emulsification Experiments.
Processes,
Vol. 9,
Issue. 12,
p.
2242.
Berny, A.
Popinet, S.
Séon, T.
and
Deike, L.
2021.
Statistics of Jet Drop Production.
Geophysical Research Letters,
Vol. 48,
Issue. 10,
Rivière, Aliénor
Ruth, Daniel J.
Mostert, Wouter
Deike, Luc
and
Perrard, Stéphane
2022.
Capillary driven fragmentation of large gas bubbles in turbulence.
Physical Review Fluids,
Vol. 7,
Issue. 8,
Qi, Yinghe
Tan, Shiyong
Corbitt, Noah
Urbanik, Carl
Salibindla, Ashwanth K. R.
and
Ni, Rui
2022.
Fragmentation in turbulence by small eddies.
Nature Communications,
Vol. 13,
Issue. 1,
Bußmann, A.
Buchmeier, J.
Dodd, M.S.
Adami, S.
and
Bermejo-Moreno, I.
2022.
Tracking and analysis of interfaces and flow structures in multiphase flows.
Computers & Fluids,
Vol. 248,
Issue. ,
p.
105665.
Begemann, Alexander
Trummler, Theresa
Trautner, Elias
Hasslberger, Josef
and
Klein, Markus
2022.
Effect of turbulence intensity and surface tension on the emulsification process and its stationary state—A numerical study.
The Canadian Journal of Chemical Engineering,
Vol. 100,
Issue. 12,
p.
3548.
Ruth, Daniel J.
Aiyer, Aditya K.
Rivière, Aliénor
Perrard, Stéphane
and
Deike, Luc
2022.
Experimental observations and modelling of sub-Hinze bubble production by turbulent bubble break-up.
Journal of Fluid Mechanics,
Vol. 951,
Issue. ,
Håkansson, Andreas
Crialesi-Esposito, Marco
Nilsson, Lars
and
Brandt, Luca
2022.
A criterion for when an emulsion drop undergoing turbulent deformation has reached a critically deformed state.
Colloids and Surfaces A: Physicochemical and Engineering Aspects,
Vol. 648,
Issue. ,
p.
129213.
Deike, Luc
2022.
Mass Transfer at the Ocean–Atmosphere Interface: The Role of Wave Breaking, Droplets, and Bubbles.
Annual Review of Fluid Mechanics,
Vol. 54,
Issue. 1,
p.
191.
Chen, Huiting
Li, Ying
Xiong, Yuandong
Wei, Han
Saxén, Henrik
and
Yu, Yaowei
2022.
Effect of particle holdup on bubble formation in suspension medium by VOF–DPM simulation.
Granular Matter,
Vol. 24,
Issue. 4,
Crialesi-Esposito, Marco
Rosti, Marco Edoardo
Chibbaro, Sergio
and
Brandt, Luca
2022.
Modulation of homogeneous and isotropic turbulence in emulsions.
Journal of Fluid Mechanics,
Vol. 940,
Issue. ,
Thaker, Abhijeet H.
and
Ranade, Vivek V.
2022.
Emulsions Using a Vortex-Based Cavitation Device: Influence of Number of Passes, Pressure Drop, and Device Scale on Droplet Size Distributions.
Industrial & Engineering Chemistry Research,
Wu, Jiarong
Popinet, Stéphane
and
Deike, Luc
2022.
Revisiting wind wave growth with fully coupled direct numerical simulations.
Journal of Fluid Mechanics,
Vol. 951,
Issue. ,
Deike, L.
Reichl, B. G.
and
Paulot, F.
2022.
A Mechanistic Sea Spray Generation Function Based on the Sea State and the Physics of Bubble Bursting.
AGU Advances,
Vol. 3,
Issue. 6,
Håkansson, Andreas
and
Brandt, Luca
2022.
Deformation and initial breakup morphology of viscous emulsion drops in isotropic homogeneous turbulence with relevance for emulsification devices.
Chemical Engineering Science,
Vol. 253,
Issue. ,
p.
117599.
Ma, Tian
Hessenkemper, Hendrik
Lucas, Dirk
and
Bragg, Andrew D.
2022.
An experimental study on the multiscale properties of turbulence in bubble-laden flows.
Journal of Fluid Mechanics,
Vol. 936,
Issue. ,
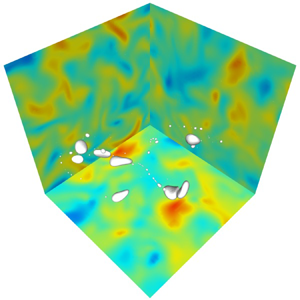
 $d_h$. At Weber number close to stable conditions (initial bubble sizes
$d_h$. At Weber number close to stable conditions (initial bubble sizes  $d_0\approx d_h$), we observe binary and tertiary break-ups, leading to bubbles mostly between
$d_0\approx d_h$), we observe binary and tertiary break-ups, leading to bubbles mostly between  $0.5d_h$ and
$0.5d_h$ and  $d_h$, a signature of a production process local in scale. For large Weber numbers (
$d_h$, a signature of a production process local in scale. For large Weber numbers ( $d_0> 3d_h$), we observe the creation of a wide range of bubble radii, with numerous child bubbles between
$d_0> 3d_h$), we observe the creation of a wide range of bubble radii, with numerous child bubbles between  $0.1d_h$ and
$0.1d_h$ and  $0.3d_h$, an order of magnitude smaller than the parent bubble. The separation of scales between the parent and child bubble is a signature of a production process non-local in scale. The formation mechanism of these sub-Hinze scale bubbles relates to rapid large deformation and successive break-ups: the first break-up in a sequence leaves highly deformed bubbles which will break again, without recovering a spherical shape and creating an array of much smaller bubbles. We discuss the application of this scenario to the production of sub-Hinze bubbles under breaking waves.
$0.3d_h$, an order of magnitude smaller than the parent bubble. The separation of scales between the parent and child bubble is a signature of a production process non-local in scale. The formation mechanism of these sub-Hinze scale bubbles relates to rapid large deformation and successive break-ups: the first break-up in a sequence leaves highly deformed bubbles which will break again, without recovering a spherical shape and creating an array of much smaller bubbles. We discuss the application of this scenario to the production of sub-Hinze bubbles under breaking waves.