Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-24T20:08:34.307Z Has data issue: false hasContentIssue false
  • English
  • Français

The structure of zonal jets in geostrophic turbulence

Published online by Cambridge University Press:  20 September 2012

Richard K. Scott  and
David G. Dritschel
Richard K. Scott*
Affiliation:
School of Mathematics and Statistics, University of St Andrews, St Andrews KY16 9SS, UK
David G. Dritschel
Affiliation:
School of Mathematics and Statistics, University of St Andrews, St Andrews KY16 9SS, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

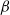The structure of zonal jets arising in forced-dissipative, two-dimensional turbulent flow on the -plane is investigated using high-resolution, long-time numerical integrations, with particular emphasis on the late-time distribution of potential vorticity. The structure of the jets is found to depend in a simple way on a single non-dimensional parameter, which may be conveniently expressed as the ratio 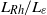, where and 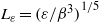are two natural length scales arising in the problem; here 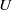may be taken as the r.m.s. velocity, 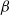is the background gradient of potential vorticity in the north–south direction, and is the rate of energy input by the forcing. It is shown that jet strength increases with 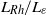, with the limiting case of the potential vorticity staircase, comprising a monotonic, piecewise-constant profile in the north–south direction, being approached for 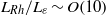. At lower values, eddies created by the forcing become sufficiently intense to continually disrupt the steepening of potential vorticity gradients in the jet cores, preventing strong jets from developing. Although detailed features such as the regularity of jet spacing and intensity are found to depend on the spectral distribution of the forcing, the approach of the staircase limit with increasing 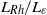is robust across a variety of different forcing types considered.

JFM classification

Geophysical and Geological Flows: Geostrophic turbulence Geophysical and Geological Flows: Quasi-geostrophic flows Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 711 , 25 November 2012 , pp. 576 - 598
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Baldwin, M. P., Rhines, P. B., Huang, H.-P. & McIntyre, M. E. 2007 The jet-stream conundrum. Science 315, 467–468.Google Scholar
2. Berloff, P., Karabasov, S., Farrar, J. T. & Kamenkovich, I. 2011 On latency of multiple zonal jets in the oceans. J. Fluid Mech. 686, 534–567.Google Scholar
3. Dritschel, D. G. 1989 Contour dynamics and contour surgery: numerical algorithms for extended, high-resolution modelling of vortex dynamics in two-dimensional, inviscid, incompressible flows. Comput. Phys. Rep. 10, 78–146.Google Scholar
4. Dritschel, D. G. & Ambaum, M. H. P. 1997 A contour-advective semi-Lagrangian numerical algorithm for simulating fine-scale conservative dynamical fields. Q. J. R. Meteorol. Soc. 123, 1097–1130.Google Scholar
5. Dritschel, D. G. & Fontane, J. 2010 The combined Lagrangian advection method. J. Comput. Phys. 229, 5408–5417.CrossRefGoogle Scholar
6. Dritschel, D. G. & McIntyre, M. E. 2008 Multiple jets as PV staircases: the Phillips effect and the resilience of eddy-transport barriers. J. Atmos. Sci. 65, 855–874.Google Scholar
7. Dritschel, D. G. & Scott, R. K. 2009 On the simulation of nearly inviscid two-dimensional turbulence. J. Comput. Phys. 228, 2707–2711.CrossRefGoogle Scholar
8. Dritschel, D. G. & Scott, R. K. 2011 Jet sharpening by turbulent mixing. Phil. Trans. R. Soc. Lond. A 369, 754–770.Google Scholar
9. Dunkerton, T. J. & Scott, R. K. 2008 A barotropic model of the angular momentum conserving potential vorticity staircase in spherical geometry. J. Atmos. Sci. 65, 1105–1136.Google Scholar
10. Fontane, J. & Dritschel, D. 2009 The HyperCASL algorithm: a new approach to the numerical simulation of geophysical flows. J. Comput. Phys. 228, 6411–6425.CrossRefGoogle Scholar
11. Galperin, B., Nakano, H., Huang, H.-P. & Sukoriansky, S. 2004 The ubiquitous zonal jets in the atmospheres of giant planets and earth’s oceans. Geophys. Res. Lett. 31, L13303.Google Scholar
12. Huang, H.-P., Galperin, B. & Sukoriansky, S. 2001 Anisotropic spectra in two-dimensional turbulence on the surface of a rotating sphere. Phys. Fluids 13, 225–240.Google Scholar
13. Maltrud, M. E. & Vallis, G. K. 1991 Energy spectra and coherent structures in forced two-dimensional and beta-plane turbulence. J. Fluid Mech. 228, 321–342.Google Scholar
14. Marcus, P. S. 1993 Jupiter’s great red spot and other vortices. Annu. Rev. Astron. Astrophys. 31, 523–573.Google Scholar
15. McIntyre, M. E. 1982 How well do we understand the dynamics of stratospheric warmings?. J. Meteorol. Soc. Japan 60, 37–65, special issue in commemoration of the centennial of the Meteorological Society of Japan, ed. K. Ninomiya.Google Scholar
16. McIntyre, M. E. 2008 Potential-vorticity inversion and the wave–turbulence jigsaw: some recent clarifications. Adv. Geosci. 15, 47–56.CrossRefGoogle Scholar
17. Panetta, R. L. 1993 Zonal jets in wide baroclinically unstable regions: persistence and scale selection. J. Atmos. Sci. 50, 2073–2106.Google Scholar
18. Peltier, W. R. & Stuhne, G. R. 2002 The upscale turbulent cascade: shear layers, cyclones and gas giant bands. In Meteorology at the Millennium (ed. Pierce, R. ). Academic.Google Scholar
19. Phillips, O. M. 1972 Turbulence in a strongly stratified fluid – is it unstable? Deep-Sea Res. 19, 79–81.Google Scholar
20. Rhines, P. B. 1975 Waves and turbulence on a beta-plane. J. Fluid Mech. 69, 417–443.Google Scholar
21. Saffman, P. G. 1971 On the spectrum and decay of random two-dimensional vorticity distributions at large Reynolds number. Stud. Appl. Maths 50, 377–383.Google Scholar
22. Scott, R. K. 2010 The structure of zonal jets in shallow water turbulence on the sphere. In IUTAM Symposium on Turbulence in the Atmosphere and Oceans (ed. Dritschel, D. G. ), IUTAM Bookseries, vol. 28 , pp. 243–252. Springer.Google Scholar
23. Scott, R. K. & Polvani, L. M. 2007 Forced-dissipative shallow water turbulence on the sphere and the atmospheric circulation of the gas planets. J. Atmos. Sci. 64, 3158–3176.CrossRefGoogle Scholar
24. Scott, R. K. & Tissier, A.-S. 2012 The generation of zonal jets by large-scale mixing. Phys. Fluids (submitted).Google Scholar
25. Sukoriansky, S., Dikovskaya, N. & Galperin, B. 2007 On the arrest of inverse energy cascade and the Rhines scale. J. Atmos. Sci. 64, 3312–3327.Google Scholar
26. Vallis, G. K. 2006 Atmospheric and Oceanic Fluid Dynamics. Cambridge University Press.Google Scholar
27. Williams, G. P. 1978 Planetary circulations: 1. Barotropic representation of Jovian and terrestrial turbulence. J. Atmos. Sci. 35, 1399–1424.Google Scholar