Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-12-01T08:08:54.419Z Has data issue: false hasContentIssue false
  • English
  • Français

Structure of high Reynolds number boundary layers over cube canopies

Published online by Cambridge University Press:  10 May 2019

Jérémy Basley Open the ORCID record for Jérémy Basley [Opens in a new window] ,
Laurent Perret  and
Romain Mathis Open the ORCID record for Romain Mathis [Opens in a new window]
Jérémy Basley*
Affiliation:
LHEEA, UMR 6598 CNRS Centrale Nantes, 44300 Nantes, France Department of Aeronautics, Imperial College London, London SW7 2AZ, UK
Laurent Perret
Affiliation:
LHEEA, UMR 6598 CNRS Centrale Nantes, 44300 Nantes, France
Romain Mathis
Affiliation:
Institut de Mécanique des Fluides de Toulouse (IMFT), Université de Toulouse, CNRS, Toulouse 31400, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The influence of a cube-based canopy on coherent structures of the flow was investigated in a high Reynolds number boundary layer (thickness 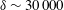$\unicode[STIX]{x1D6FF}\sim 30\,000$ wall units). Wind tunnel experiments were conducted considering wall configurations that represent three idealised urban terrains. Stereoscopic particle image velocimetry was employed using a large field of view in a streamwise–spanwise plane (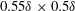$0.55\unicode[STIX]{x1D6FF}\times 0.5\unicode[STIX]{x1D6FF}$) combined to two-point hot-wire measurements. The analysis of the flow within the inertial layer highlights the independence of its characteristics from the wall configuration. The population of coherent structures is in agreement with that of smooth-wall boundary layers, i.e. consisting of large- and very-large-scale motions, sweeps and ejections, as well as smaller-scale vortical structures. The characteristics of vortices appear to be independent of the roughness configuration while their spatial distribution is closely linked to large meandering motions of the boundary layer. The canopy geometry only significantly impacts the wall-normal exchanges within the roughness sublayer. Bi-dimensional spectral analysis demonstrates that wall-normal velocity fluctuations are constrained by the presence of the canopy for the densest investigated configurations. This threshold in plan area density above which large scales from the overlying boundary layer can penetrate the roughness sublayer is consistent with the change of the flow regime reported in the literature and constitutes a major difference with flows over vegetation canopies.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Boundary Layers: Boundary layer structure Turbulent Flows: Turbulence modelling
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 870 , 10 July 2019 , pp. 460 - 491
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J., Christensen, K. T. & Liu, Z.-C. 2000 Analysis and interpretation of instantaneous turbulent velocity fields. Exp. Fluids 29, 275–290.Google Scholar
Ahn, J., Lee, J. H. & Sung, H. J. 2013 Statistics of the turbulent boundary layers over 3D cube-roughened walls. Intl J. Heat Fluid Flow 44, 394–402.Google Scholar
Amir, M. & Castro, I. P. 2011 Turbulence in rough-wall boundary layers: universality issues. Exp. Fluids 51 (2), 313–326.Google Scholar
Anderson, W. 2016 Amplitude modulation of streamwise velocity fluctuations in the roughness sublayer: evidence from large-eddy simulations. J. Fluid Mech. 789, 567–588.Google Scholar
Anderson, W., Li, Q. & Bou-Zeid, E. 2015 Numerical simulation of flow over urban-like topographies and evaluation of turbulence temporal attributes. J. Turbul. 16 (9), 809–831.Google Scholar
Atkinson, C., Buchmann, N. A. & Soria, J. 2015 An experimental investigation of turbulent convection velocities in a turbulent boundary layer. Flow Turbul. Combust. 94, 79–95.Google Scholar
Baars, W. J., Hutchins, N. & Marusic, I. 2017 Self-similarity of wall-attached turbulence in boundary layers. J. Fluid Mech. 823, R2.Google Scholar
Basley, J., Perret, L. & Mathis, R. 2018 Spatial modulations of kinetic energy in the roughness sublayer. J. Fluid Mech. 850, 584–610.Google Scholar
Bendat, J. S. & Piersol, A. G. 2010 Random Data, 4th edn. John Wiley and Sons.Google Scholar
Blackman, K. & Perret, L. 2016 Non-linear interactions in a boundary layer developing over an array of cubes using stochastic estimation. Phys. Fluids 28, 095108.Google Scholar
Blackman, K., Perret, L., Calmet, I. & Rivet, C. 2017 Turbulent kinetic energy budget in the boundary layer developing over an urban-like rough wall using PIV. Phys. Fluids 29, 085113.Google Scholar
Brunet, Y., Finnigan, J. J. & Raupach, M. R. 1994 A wind tunnel study of air flow in waving wheat: single-point statistics. Boundary-Layer Meteorol. 70, 95–132.Google Scholar
Castro, I. P., Cheng, H. & Reynolds, R. 2006 Turbulence over urban-type roughness: deductions from wind-tunnel measurements. Boundary-Layer Meteorol. 118, 109–131.Google Scholar
Castro, I. P., Segalini, A. & Alfredsson, P. H. 2013 Outer-layer turbulence intensities in smooth- and rough-wall boundary layers. J. Fluid Mech. 727, 119–131.Google Scholar
Chandran, D., Baidya, R., Monty, J. P. & Marusic, I. 2017 Two-dimensional energy spectra in high-Reynolds-number turbulent boundary layers. J. Fluid Mech. 826, R1.Google Scholar
Cheng, H. & Castro, I. P. 2002 Near wall flow over urban-like roughness. Boundary-Layer Meteorol. 104, 229–259.Google Scholar
Cheng, H., Hayden, P., Robins, A. G. & Castro, I. P. 2007 Flow over cube arrays of different packing densities. J. Wind Engng Ind. Aerodyn. 95 (8), 715–740.Google Scholar
Christen, A., van Gorsel, E. & Vogt, R. 2007 Coherent structures in urban roughness sublayer turbulence. Intl J. Climatol. 27, 1955–1968.Google Scholar
Coceal, O., Dobre, A., Thomas, T. G. & Belcher, S. E. 2007 Structure of turbulent flow over regular arrays of cubical roughness. J. Fluid Mech. 589, 375–409.Google Scholar
DeGraaff, D. B. & Eaton, J. K. 2000 Reynolds number scaling of the flat plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.Google Scholar
Del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.Google Scholar
Dennis, D. J. C. & Nickels, T. B. 2008 On the limitations of Taylor’s hypothesis in constructing long structures in a turbulent boundary layer. J. Fluid Mech. 614, 197–206.Google Scholar
Dennis, D. J. C. & Nickels, T. B. 2011 Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 2. Long structures. J. Fluid Mech. 673, 218–244.Google Scholar
Finnigan, J. J. 2000 Turbulence in plant canopies. Annu. Rev. Fluid Mech. 32, 519–571.Google Scholar
Flack, K., Schultz, M. P. & Connelly, J. S. 2007 Examination of a critical roughness height for outer layer similarity. Phys. Fluids 19, 095104.Google Scholar
Florens, E., Eiff, O. & Moulin, F. 2013 Defining the roughness sublayer and its turbulence statistics. Exp. Fluids 54, 1500.Google Scholar
Grimmond, C. S. B. & Oke, T. R. 1999 Aerodynamic properties of urban areas derived from analysis of surface form. J. Appl. Meteorol. 38, 1262–1292.Google Scholar
Hagishima, A., Tanimoto, J., Nagayama, K. & Meno, S. 2009 Aerodynamic parameters of regular arrays of rectangular blocks with various geometries. Boundary-Layer Meteorol. 132, 315–337.Google Scholar
Huang, G., Simoëns, S., Vinkovic, I., Ribault, C. L., Dupont, S. & Bergametti, G. 2016 Law-of-the-wall in a boundary-layer over regularly distributed roughness elements. J. Turbul. 17 (5), 518–541.Google Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Inagaki, A., Castillo, M. C. L., Yamashita, Y., Kanda, M. & Takimoto, H. 2012 Large-eddy simulation of coherent flow structures within a cubical canopy. Boundary-Layer Meteorol. 142, 207–222.Google Scholar
Inagaki, A. & Kanda, M. 2008 Turbulent flow similarity over an array of cubes in near-neutrally stratified atmospheric flow. J. Fluid Mech. 615, 101–120.Google Scholar
Inagaki, A. & Kanda, M. 2010 Organized structure of active turbulence over an array of cubes within the logarithmic layer of atmospheric flow. Boundary-Layer Meteorol. 135 (2), 209–228.Google Scholar
Jackson, P. S. 1981 On the displacement height in the logarithmic velocity profile. J. Fluid Mech. 111, 15–25.Google Scholar
Jiménez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.Google Scholar
Jiménez, J., Del Álamo, J. C. & Flores, O. 2004 The large-scale dynamics of near-wall turbulence. J. Fluid Mech. 505, 179–199.Google Scholar
Kanda, M. 2006 Large-eddy simulations on the effects of surface geometry of building arrays on turbulent organized structures. Boundary-Layer Meteorol. 118, 151–168.Google Scholar
Kanda, M., Kanega, M. K., Kawai, T. K., Moriwaki, R. & Sugawara, H. 2007 Roughness lengths for momentum and heat derived from outdoor urban scale models. J. Appl. Meteorol. Climatol. 47, 1067–1079.Google Scholar
Kanda, M., Moriwaki, R. & Kasamatsu, F. 2004 Large eddy simulation of turbulent organized structure within and above explicitly resolved cubic arrays. Boundary-Layer Meteorol. 112, 343–368.Google Scholar
Krogstad, P. A., Kaspersen, J. H. & Rimestad, S. 1998 Convection velocities in a turbulent boundary layer. Phys. Fluids 10 (4), 949–957.Google Scholar
Lee, J. H., Seena, A., Lee, S.-H. & Sung, H. J. 2012 Turbulent boundary layers over rod- and cube-roughened walls. J. Turbul. 13 (1), N40.Google Scholar
Lee, J. H., Sung, H. J. & Krogstad, P.-A. 2011 Direct numerical simulation of the turbulent boundary layer over a cube-roughened wall. J. Fluid Mech. 669, 397–431.Google Scholar
Leonardi, S. & Castro, I. P. 2010 Channel flow over large cube roughness: a direct numerical simulation study. J. Fluid Mech. 651, 519–539.Google Scholar
Leonardi, S., Orlandi, P., Smalley, R., Djenidi, L. & Antonia, R. A. 2003 Direct numerical simulations of turbulent channel flow with transverse square bars on one wall. J. Fluid Mech. 491, 229–238.Google Scholar
Macdonald, R. W., Griffiths, R. F. & Hall, D. J. 1998 An improved method for estimation of surface roughness of obstacle arrays. Atmos. Environ. 32, 857–1864.Google Scholar
Marusic, I. & Hutchins, N. 2008 Study of the log-layer structure in wall turbulence over a very large range of Reynolds number. Flow Turbul. Combust. 81 (1), 115–130.Google Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010a Predictive model for wall-bounded turbulent flow. Science 329, 193–196.Google Scholar
Marusic, I., McKeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. 2010b Wall-bounded turbulent flows at high Reynolds numbers: recent advances and key issues. Phys. Fluids 22 (6), 065103.Google Scholar
Marusic, I., Monty, J., Hultmark, M. & Smits, A. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
McNaughton, K. G. & Brunet, Y. 2002 Tonwsend’s hypothesis, coherent structures and Monin–Obukhov similarity. Boundary-Layer Meteorol. 102, 161–175.Google Scholar
Nadeem, M., Lee, J. H., Lee, J. & Sung, H. J. 2015 Turbulent boundary layers over sparsely-spaced rod-roughened walls. Intl J. Heat Fluid Flow 56, 16–27.Google Scholar
Oke, T. R. 1988 Street design and urban canopy layer climate. Eng. Build 11, 103–113.Google Scholar
Panton, R. L. 2001 Overview of the self-sustaining mechanisms of wall turbulence. Prog. Aerosp. Sci. 37, 341–383.Google Scholar
Perret, L., Basley, J., Mathis, R. & Piquet, T. 2019 Atmospheric boundary layers over urban-like terrains: influence of the plan density on the roughness sublayer dynamics. Boundary-Layer Meteorol. 170 (2), 205–234.Google Scholar
Perry, A. E., Henbest, S. & Chong, M. S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.Google Scholar
Piringer, M., Grimmond, C. S. B., Joffre, S. M., Mestayer, P., Middleton, D. R., Rotach, M. W., Baklanov, A., De Ridder, K., Ferreira, J., Guilloteau, E. et al. 2002 Investigating the surface energy balance in urban areas – recent advances and future needs. Water, Air Soil Pollution 2 (5–6), 1–16.Google Scholar
Placidi, M. & Ganapathisubramani, B. 2015 Effects of frontal and plan solidities on aerodynamic parameters and the roughness sublayer in turbulent boundary layers. J. Fluid Mech. 782, 541–566.Google Scholar
Placidi, M. & Ganapathisubramani, B. 2017 Turbulent flow over large roughness elements: effect of frontal and plan solidity on turbulence statistics and structure. Boundary-Layer Meteorol. 167, 99–121.Google Scholar
Raupach, M. R., Hughes, D. E. & Cleugh, H. A. 2006 Momentum absorption in rough-wall boundary layers with sparse roughness elements in random and clustered distributions. Boundary-Layer Meteorol. 120, 201–218.Google Scholar
Reynolds, R. T. & Castro, I. P. 2008 Near wall flow over urban-like roughness. Exp. Fluids 45, 141–156.Google Scholar
Shaw, R. H., Brunet, Y., Finnigan, J. J. & Raupach, M. R. 1995 A wind tunnel study of air flow in waving wheat: two point velocity statistics. Boundary-Layer Meteorol. 76, 349–376.Google Scholar
Snyder, W. H. & Castro, I. P. 2002 The critical Reynolds number for rough-wall boundary layers. J. Wind Engng Ind. Aerodyn. 90, 41–54.Google Scholar
Squire, D. T., Morill-Winter, C., Hutchins, N., Schultz, M. P., Klewicki, J. C. & Marusic, I. 2016 Comparison of turbulent boundary layers over smooth and rough surfaces up to high Reynolds numbers. J. Fluid Mech. 795, 210–240.Google Scholar
Takimoto, H., Inagaki, A., Kanda, M., Sato, A. & Michioka, T. 2013 Length-scale similarity of turbulent organized structures over surfaces with different roughness types. Boundary-Layer Meteorol. 147 (2), 217–236.Google Scholar
Taylor, G. I. 1938 The spectrum of turbulence. Proc. R. Soc. Lond. A 164, 476–490.Google Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Volino, R. J., Schultz, M. P. & Flack, K. A. 2007 Turbulence structure in rough- and smooth-wall boundary layers. J. Fluid Mech. 592, 263–293.Google Scholar
Volino, R. J., Schultz, M. P. & Flack, K. A. 2011 Turbulence structure in boundary layers over periodic two- and three-dimensional roughness. J. Fluid Mech. 676, 172–190.Google Scholar
Welch, P. D. 1967 The use of fast Fourier treansform for the estimation of power spectra: a method based on time averaging over short, modified periodograms. In Modern Spectrum Analysis, pp. 17–20. IEEE Press.Google Scholar
Wu, O. & Christensen, K. T. 2010 Spatial structure of a turbulent boundary layer with irregular surface roughness. J. Fluid Mech. 655, 380–418.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar