The structure of a turbulent line fountain

Abstract

Line fountains form when heavy miscible fluid is ejected steadily upwards as a jet from a high-aspect-ratio rectangular slot, of length 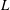$L$ and half-width 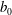$b_{0}$, into lighter quiescent surroundings. Viewed along the slot from one end, previous observations reveal that the ejected fluid mixes with the environment and reaches a peak height before partially collapsing back downward under gravity to form a fountain whose top thereafter fluctuates vertically about a mean height. While the motion as perceived from this single view has provided insights that have successfully guided theoretical predictions for the initial rise height, until now a wider understanding of line fountains, and corresponding predictive capability, has been limited to this single prediction due to a lack of any other observational data. Indeed, the general behaviour of line fountains, including the structure internally and along the spanwise length 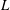$L$ of the slot, has not been reported previously. To address this, flow visualisations and comprehensive measurements of saline fountains in an aqueous environment are presented here that reveal their complex overall structure and behaviours. After establishing the uniformity of the source conditions from slots of aspect ratio 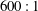$600:1$ and 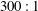$300:1$, we first show that double-averaged (spanwise and time) rise heights 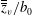$\overline{\overline{z}}_{v}/b_{0}$ scale on 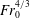$Fr_{0}^{4/3}$, 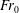$Fr_{0}$ being the source Froude number, with vertical fluctuations being circa 20 % of these heights. Then, simultaneously interrogating the flow as viewed from above and from the side onto the spanwise dimension, we identify three distinct patterns of behaviour. Instrumental to distinguishing these behaviours were the contrasting signatures we observed in the time series of rise height departures from the mean which led us to the following classification: (i) non-uniform flapping for 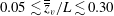$0.05\lesssim \overline{\overline{z}}_{v}/L\lesssim 0.30$, in which the lateral motion of the fountain takes the form of an oscillatory wave with a wavelength of 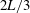$2L/3$ (approx.); (ii) uniform flapping for 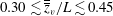$0.30\lesssim \overline{\overline{z}}_{v}/L\lesssim 0.45$, in which the entire fountain sways to the left and then to the right side of the slot; and (iii) disorganised flapping for 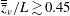$\overline{\overline{z}}_{v}/L\gtrsim 0.45$. Regarding the internal structure, we show that unlike a classic round fountain, eddying structures comparable in scale with the rise height form towards the top of the fountain, and the counterflow forms predominantly to one side of the jet. We then identify the single dominant mechanism driving the flapping motions, successfully linking the wave-like behaviour observed along the span to the internal structure and vertical oscillations. Quantifying the oscillatory motions, both the vertical and flapping frequencies scale as 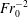$Fr_{0}^{-2}$, and we demonstrate and explain a robust coupling between these frequencies that follows a ratio of 2:1.