Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-02-11T12:04:35.929Z Has data issue: false hasContentIssue false
  • English
  • Français

Structural organization of large and very large scales in turbulent pipe flow simulation

Published online by Cambridge University Press:  27 February 2013

J. R. Baltzer ,
R. J. Adrian  and
Xiaohua Wu
J. R. Baltzer
Affiliation:
School for Engineering of Matter, Transport and Energy, Arizona State University, P.O. Box 876106, Tempe, AZ 85287-6106, USA
R. J. Adrian*
Affiliation:
School for Engineering of Matter, Transport and Energy, Arizona State University, P.O. Box 876106, Tempe, AZ 85287-6106, USA
Xiaohua Wu
Affiliation:
Department of Mechanical Engineering, Royal Military College of Canada, Kingston, Ontario, Canada K7K 7B4
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The physical structures of velocity are examined from a recent direct numerical simulation of fully developed incompressible turbulent pipe flow (Wu, Baltzer & Adrian, J. Fluid Mech., vol. 698, 2012, pp. 235–281) at a Reynolds number of 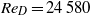${\mathit{Re}}_{D} = 24\hspace{0.167em} 580$ (based on bulk velocity) and a Kármán number of 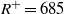${R}^{+ } = 685$. In that work, the periodic domain length of 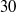$30$ pipe radii 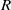$R$ was found to be sufficient to examine long motions of negative streamwise velocity fluctuation that are commonly observed in wall-bounded turbulent flows and correspond to the large fractions of energy present at very long streamwise wavelengths (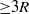${\geq }3R$). In this paper we study how long motions are composed of smaller motions. We characterize the spatial arrangements of very large-scale motions (VLSMs) extending through the logarithmic layer and above, and we find that they possess dominant helix angles (azimuthal inclinations relative to streamwise) that are revealed by two- and three-dimensional two-point spatial correlations of velocity. The correlations also reveal that the shorter, large-scale motions (LSMs) that concatenate to comprise the VLSMs are themselves more streamwise aligned. We show that the largest VLSMs possess a form similar to roll cells centred above the logarithmic layer and that they appear to play an important role in organizing the flow, while themselves contributing only a minor fraction of the flow turbulent kinetic energy. The roll cell motions play an important role with the smaller scales of motion that are necessary to create the strong streamwise streaks of low-velocity fluctuation that characterize the flow.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 720 , 10 April 2013 , pp. 236 - 279
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 1996 Stochastic estimation of the structure of turbulent fields. In Eddy Structure Identification (ed. Bonnet, J. P.), pp. 145–195. Springer.CrossRefGoogle Scholar
Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19, 041301.Google Scholar
Adrian, R. J. & Liu, Z.-C. 2002 Observation of vortex packets in direct numerical simulation of fully turbulent channel flow. J. Vis. 5, 9–19.CrossRefGoogle Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.CrossRefGoogle Scholar
del Álamo, J. C. & Jiménez, J. 2006 Linear energy amplification in turbulent channels. J. Fluid Mech. 559, 205–213.Google Scholar
del Álamo, J. C. & Jiménez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5–26.CrossRefGoogle Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2006 Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 561, 329–358.Google Scholar
Aubry, N., Holmes, P., Lumley, J. L. & Stone, E. 1988 The dynamics of coherent structures in the wall region of a turbulent boundary layer. J. Fluid Mech. 192, 115–173.Google Scholar
Bailey, S. C. C., Hultmark, M., Smits, A. J. & Schultz, M. P. 2008 Azimuthal structure of turbulence in high Reynolds number pipe flow. J. Fluid Mech. 615, 121–138.Google Scholar
Bailey, S. C. C. & Smits, A. J. 2010 Experimental investigation of the structure of large- and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 651, 339–356.Google Scholar
Balachandar, S. & Adrian, R. J. 1993 Structure extraction by stochastic estimation with adaptive events. Theor. Comput. Fluid Dyn. 5, 243–257.Google Scholar
Balakumar, B. J. & Adrian, R. J. 2007 Large- and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. A 365, 665–681.Google Scholar
Baltzer, J. R. 2012 Structure and proper orthogonal decomposition in simulations of wall-bounded turbulent shear flows with canonical geometries. PhD thesis, Arizona State University.Google Scholar
Baltzer, J. R. & Adrian, R. J. 2011 Structure, scaling, and synthesis of proper orthogonal decomposition modes of inhomogeneous turbulence. Phys. Fluids 23, 015107.Google Scholar
Chin, C., Ooi, A. S. H., Marusic, I. & Blackburn, H. M. 2010 The influence of pipe length on turbulence statistics computed from direct numerical simulation data. Phys. Fluids 22, 115107.CrossRefGoogle Scholar
Christensen, K. T. & Adrian, R. J. 2001 Statistical evidence of hairpin vortex packets in wall turbulence. J. Fluid Mech. 431, 433–443.Google Scholar
Chung, D. & McKeon, B. J. 2010 Large-eddy simulation of large-scale structures in long channel flow. J. Fluid Mech. 661, 341–364.Google Scholar
Delo, C. J., Kelso, R. M. & Smits, A. J. 2004 Three-dimensional structure of a low-Reynolds-number turbulent boundary layer. J. Fluid Mech. 512, 47–83.CrossRefGoogle Scholar
Dennis, D. J. C. & Nickels, T. B. 2008 On the limitations of Taylor’s hypothesis in constructing long structures in a turbulent boundary layer. J. Fluid Mech. 614, 197–206.Google Scholar
Dennis, D. J. C. & Nickels, T. B. 2011 Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 2. Long structures. J. Fluid Mech. 673, 218–244.Google Scholar
Duggleby, A., Ball, K. S., Paul, M. R. & Fischer, P. F. 2007 Dynamical eigenfunction decomposition of turbulent pipe flow. J. Turbul. 8 (43), 1–24.Google Scholar
Duggleby, A., Ball, K. S. & Schwaenen, M. 2009 Structure and dynamics of low Reynolds number turbulent pipe flow. Phil. Trans. R. Soc. A 367, 473–488.Google Scholar
Duggleby, A. & Paul, M. R. 2010 Computing the Karhunen–Loève dimension of an extensively chaotic flow field given a finite amount of data. Comput. Fluids 39 (9), 1704–1710.CrossRefGoogle Scholar
Eckhardt, B., Schneider, T. M., Hof, B. & Westerweel, J. 2007 Turbulence transition in pipe flow. Annu. Rev. Fluid Mech. 39, 447–468.Google Scholar
Eggels, J. G. M., Unger, F., Weiss, M. H., Westerweel, J., Adrian, R. J., Friedrich, R. & Nieuwstadt, F. T. M. 1994 Fully developed turbulent pipe flow: a comparison between direct numerical simulation and experiment. J. Fluid Mech. 268, 175–210.Google Scholar
Elsinga, G. E., Adrian, R. J., van Oudheusden, B. W. & Scarano, F. 2010 Three-dimensional vortex organization in a high-Reynolds-number supersonic turbulent boundary layer. J. Fluid Mech. 644, 35–60.Google Scholar
Farrell, B. F. & Ioannou, P. J. 2012 Dynamics of streamwise rolls and streaks in turbulent wall-bounded shear flow. J. Fluid Mech. 708, 149–196.Google Scholar
Ganapathisubramani, B., Clemens, N. T. & Dolling, D. S. 2006 Large-scale motions in a supersonic turbulent boundary layer. J. Fluid Mech. 556, 271–282.CrossRefGoogle Scholar
Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478, 35–46.Google Scholar
Gro ße, S. & Westerweel, J. 2011 Investigation of large-scale coherent motion in turbulent pipe flow by means of time resolved stereo-PIV. In The Ninth International Symposium on Particle Image Velocimetry (PIV’11), Kobe, Japan, 21–23 July 2011.Google Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.Google Scholar
Hambleton, W. T., Hutchins, N. & Marusic, I. 2006 Simultaneous orthogonal-plane particle image velocimetry measurements in a turbulent boundary layer. J. Fluid Mech. 560, 53–64.Google Scholar
Hanratty, T. J. & Papavassiliou, D. V. 1997 The role of wall vortices in producing turbulence. In Self-Sustaining Mechanisms of Wall Turbulence (ed. Panton, R.), pp. 83–108. Computational Mechanics Publications.Google Scholar
Hellström, L. H. O., Sinha, A. & Smits, A. J. 2011 Visualizing the very-large-scale motions in turbulent pipe flow. Phys. Fluids 23, 011703.CrossRefGoogle Scholar
Hof, B., van Doorne, Casimir W. H., Westerweel, J., Nieuwstadt, F. T. M., Faisst, H., Eckhardt, B., Wedin, H., Kerswell, R. R. & Waleffe, F. 2004 Experimental observation of nonlinear travelling waves in turbulent pipe flow. Science 305 (5690), 1594–1598.Google Scholar
Hutchins, N., Hambleton, W. T. & Marusic, I. 2005 Inclined cross-stream stereo particle image velocimetry measurements in turbulent boundary layers. J. Fluid Mech. 541, 21–54.Google Scholar
Hutchins, N. & Marusic, I. 2007a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Hutchins, N. & Marusic, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. A 365, 647–664.Google Scholar
Hutchins, N., Monty, J. P., Ganapathisubramani, B., Ng, H. C. H. & Marusic, I. 2011 Three-dimensional conditional structure of a high-Reynolds-number turbulent boundary layer. J. Fluid Mech. 673, 255–285.CrossRefGoogle Scholar
Jeong, J., Hussain, F., Schoppa, W. & Kim, J. 1997 Coherent structures near the wall in a turbulent channel flow. J. Fluid Mech. 332, 185–214.Google Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.Google Scholar
Johansson, A. V., Alfredsson, P. H. & Kim, J. 1991 Evolution and dynamics of shear-layer structures in near-wall turbulence. J. Fluid Mech. 224, 579–599.Google Scholar
Kim, H. T., Kline, S. J. & Reynolds, W. C. 1971 The production of turbulence near a smooth wall in a turbulent boundary layer. J. Fluid Mech. 50, 133–160.Google Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11, 417–422.CrossRefGoogle Scholar
Kline, S. J. & Robinson, S. K. 1989 Quasi-coherent structures in the turbulent boundary layer. Part I: Status report on a community-wide summary of the data. In Near Wall Turbulence (ed. Kline, S. J. & Afgan, N. H.), pp. 218–247. Hemisphere.Google Scholar
Lee, J. H. & Sung, H. J. 2011 Very-large-scale motions in a turbulent boundary layer. J. Fluid Mech. 673, 80–120.CrossRefGoogle Scholar
Lekakis, I. C. 1988 Coherent structures in fully developed turbulent pipe flow. PhD thesis, University of Illinois at Urbana-Champaign.Google Scholar
Lumley, J. L. 1967 The structure of inhomogeneous turbulent flows. In Atmospheric Turbulence and Radio Wave Propagation (ed. Yaglom, A. M. & Tatarsky, V. I.), pp. 166–178. Nauka.Google Scholar
Lumley, J. L. 1981 Coherent structures in turbulence. In Transition and Turbulence (ed. Meyer, R. E.), pp. 215–241. Academic.CrossRefGoogle Scholar
Marusic, I. 2001 On the role of large-scale structures in wall turbulence. Phys. Fluids 13, 735–743.Google Scholar
Marusic, I. & Adrian, R. J. 2013 Scaling issues and the role of organized motion in wall turbulence. In Ten Chapters in Turbulence (ed. Davidson, P. A., Kaneda, Y. & Sreenivasan, K. R.), Cambridge University Press.Google Scholar
Marusic, I. & Hutchins, N. 2008 Study of the log-layer structure in wall turbulence over a very large range of Reynolds number. Flow Turbul. Combust. 81, 115–130.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009a Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Mathis, R., Monty, J. P., Hutchins, N. & Marusic, I. 2009b Comparison of large-scale amplitude modulation in turbulent boundary layers, pipes, and channel flows. Phys. Fluids 21, 111703.Google Scholar
McKeon, B. J. & Sharma, A. S. 2010 A critical-layer framework for turbulent pipe flow. J. Fluid Mech. 658, 336–382.Google Scholar
Mito, Y., Hanratty, T. J., Zandonade, P. & Moser, R. D. 2007 Flow visualization of superbursts and of the log-layer in a DNS at ${\mathit{Re}}_{\tau } = 950$ . Flow Turbul. Combust. 79, 175–189.Google Scholar
Monty, J. P., Stewart, J. A., Williams, R. C. & Chong, M. S. 2007 Large-scale features in turbulent pipe and channel flows. J. Fluid Mech. 589, 147–156.Google Scholar
Moser, R. D. 1994 Kolmogorov inertial range spectra for inhomogeneous turbulence. Phys. Fluids 6 (2), 794–801.Google Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.Google Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.CrossRefGoogle Scholar
Smith, C. R. & Metzler, S. P. 1983 The characteristics of low-speed streaks in the near-wall region of a turbulent boundary layer. J. Fluid Mech. 129, 27–54.Google Scholar
Toh, S. & Itano, T. 2005 Interaction between a large-scale structure and near-wall structures in channel flow. J. Fluid Mech. 524, 249–262.Google Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Volino, R. J., Schultz, M. P. & Flack, K. A. 2007 Turbulence structure in rough- and smooth-wall boundary layers. J. Fluid Mech. 592, 263–293.Google Scholar
Wu, X., Baltzer, J. R. & Adrian, R. J. 2012 Direct numerical simulation of a $30R$ long turbulent pipe flow at ${R}^{+ } = 685$ : large- and very large-scale motions. J. Fluid Mech. 698, 235–281.Google Scholar
Wu, Y. & Christensen, K. T. 2006 Population trends of spanwise vortices in wall turbulence. J. Fluid Mech. 568, 55–76.Google Scholar
Wu, X. & Moin, P. 2008 A direct numerical simulation study on the mean velocity characteristics in turbulent pipe flow. J. Fluid Mech. 608, 81–112.CrossRefGoogle Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar
Supplementary material: PDF

Baltzer et al. supplementary material

Supplementary material

Download Baltzer et al. supplementary material(PDF)
PDF 1.1 MB