Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-24T21:03:22.177Z Has data issue: false hasContentIssue false
  • English
  • Français

Strong swirl approximation and intensive vortices in the atmosphere

Published online by Cambridge University Press:  05 December 2013

A. Y. Klimenko
A. Y. Klimenko*
Affiliation:
School of Mechanical and Mining Engineering (SoMME), The University of Queensland, St Lucia, Brisbane, QLD 4072, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This work investigates intensive vortices, which are characterised by the existence of a converging radial flow that significantly intensifies the flow rotation. Evolution and amplification of the vorticity present in the flow play important roles in the formation of the vortex. When rotation in the flow becomes sufficiently strong (this implies the validity of the strong swirl approximation, which has been developed in a series of publications since the 1950s) the previous analysis of the author and the present work determine that further amplification of vorticity is moderated by interactions of vorticity and velocity. This imposes physical constraints on the flow, resulting in the so-called compensating regime, where the radial distribution of the axial vorticity is characterised by the 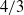$4/ 3$ and 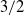$3/ 2$ power laws. This asymptotic treatment of a strong swirl is based on vorticity equations and involves higher-order terms. This treatment incorporates multi-scale analysis indicating downstream relaxation of the flow to the compensating regime. The present work also investigates and takes into account viscous and transient effects. One of the main points of this work is the applicability of the power laws of the compensating regime to intermediate regions in large atmospheric vortices, such as tropical cyclones and tornadoes.

JFM classification

Vortex Flows: Vortex Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 738 , 10 January 2014 , pp. 268 - 298
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alekseenko, S. V., Kuibin, P. A., Okulov, V. L. & Shtork, S. I. 1999 Helical vortices in swirl flow. J. Fluid Mech. 382, 195–243.CrossRefGoogle Scholar
Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Benjamin, T. B. 1962 Theory of the vortex breakdown phenomenon. J. Fluid Mech. 14, 593–629.Google Scholar
Bluestein, H. B. & Golden, J. H. 1993 Review of tornado observations. In Tornado: Its Structure, Dynamics, Prediction and Hazards, Geophysical Monograph, vol. 79, pp. 319–352. American Geophysical Union.CrossRefGoogle Scholar
Brooks, H. E., Doswell, C. A. & Davies-Jones, R. 1993 Environmental helocity and the maintenance and evolution of low-level mesocyclones. In Tornado: Its Structure, Dynamics, Prediction and Hazards, Geophysical Monograph, vol. 79, pp. 97–104. American Geophysical Union.CrossRefGoogle Scholar
Burgers, J. M. 1940 Application of a model system to illustrate some points of the statistical theory of free turbulence. Proc. K. Ned. Akad. Wet. XLIII, 2–12.Google Scholar
Cai, H. 2005 Comparison between tornadic and nontornadic mesocyclones using the vorticity (pseudovorticity) line technique. Mon. Weath. Rev. 133, 2535–2551.Google Scholar
Chan, J. C. L. 2005 The physics of tropical cyclone motion. Annu. Rev. Fluid Mech. 37, 99–128.Google Scholar
Chuah, K. H., Kuwana, K., Saito, K. & Williams, F. A. 2011 Inclined fire whirls. Proc. Combust. Inst. 32, 2417–2424.Google Scholar
Church, C. R. & Snow, J. T. 1993 Laboratory models of tornadoes. In Tornado: Its Structure, Dynamics, Prediction and Hazards, Geophysical Monograph, vol. 79, pp. 277–295. American Geophysical Union.Google Scholar
Davies-Jones, R. P., Trapp, R. J. & Bluestein, H. B. 2001 Tornadoes and tornadic storms. In Severe Convective Storms, Meteorological Monograph No. 50, pp. 167–221. American Meteorological Society.Google Scholar
Dowell, D. C. & Bluestein, H. B. 2002 The 8 June 1995 McLean, Texas, storm. Mon. Weath. Rev. 130, 2626–2670.Google Scholar
Dyudina, U. A., Flasar, F. M., Simon-Miller, A. A., Fletcher, L. N., Ingersoll, A. P., Ewald, S. P., Vasavada, A. R., West, R. A., Del Genio, A. D., Barbara, J. M., Porco, C. C. & Achterberg, R. K. 2008 Dynamics of Saturn’s south polar vortex. Science 319 (5871), 1801.Google Scholar
Einstein, H. A. & Li, H. 1951 Steady vortex flow in a real fluid. Proc. Heat Transfer Fluid Mech. Inst. 4, 33–42.Google Scholar
Emanuel, K. A. 1986 An air–sea interaction theory for tropical cyclones. Part I: steady state maintenance. J. Atmos. Sci. 43, 2044–2061.2.0.CO;2>CrossRefGoogle Scholar
Emanuel, K. 2003 Tropical cyclones. Annu. Rev. Earth Planet. Sci. 31, 75–104.CrossRefGoogle Scholar
Escudier, M. P., Bornstein, J. & Maxworthy, T. 1982 The dynamics of confined vortices. Proc. R. Soc. Lond. A 382 (1783), 335–360.Google Scholar
Fernandez-Feria, R., de la Mora, J. F. & Barrero, A. 1995 Solution breakdown in a family of self-similar nearly inviscid axisymmetric vortices. J. Fluid Mech. 305, 77–91.CrossRefGoogle Scholar
Fujita, T. T. 1981 Tornadoes and downbursts in the context of generalized planetary scales. J. Atmos. Sci. 38, 1511–1534.Google Scholar
Gray, W. M. 1973 Feasibility of beneficial hurricane modification by carbon dust seeding. Atmospheric Science Paper No. 196, Department of Atmospheric Science, Colorado State University.Google Scholar
Hawkins, H. F. & Imbembo, S. M. 1973 The structure of small intense hurricane – Inez 1966. Mon. Weath. Rev. 104, 418–422.Google Scholar
Hawkins, H. F. & Rubsam, D. T. 1968 Hurricane Hilda, 1964. Mon. Weath. Rev. 96, 617–636.Google Scholar
van Heijst, G. J. F. & Clercx, H. J. H. 2009 Laboratory modelling of geophysical vortices. Annu. Rev. Fluid Mech. 41, 143–164.Google Scholar
Holland, G. J. 1995 Scale interaction in the Western Pacific Monsoon. Meteorol. Atmos. Phys. 56, 57–79.Google Scholar
Houze, R. A. Jr., Chen, S. S., Smull, B. F., Lee, W.-C. & Bell, M. M. 2007 Hurricane intensity and eyewall replacement. Science 315, 1235–1239.CrossRefGoogle ScholarPubMed
Hughes, L. A. 1952 On the low-level structure of tropical storms. J. Meteorol. 9, 422–428.Google Scholar
Klemp, J. B. 1987 Dynamics of tornadic thunderstorms. Annu. Rev. Fluid Mech. 19, 369–402.Google Scholar
Klimenko, A. Y. 2001a Moderately strong vorticity in a bathtub-type flow. Theor. Comput. Fluid Mech. 14, 243–257.Google Scholar
Klimenko, A. Y. 2001b Near-axis asymptote of the bathtub-type inviscid vortical flows. Mech. Res. Commun. 28, 207–212.Google Scholar
Klimenko, A. Y. 2001c A small disturbance in the strong vortex flow. Phys. Fluids 13, 1815–1818.Google Scholar
Klimenko, A. Y. 2007 Do we find hurricanes on other planets? In Proc. 16th Australian Fluid Mechanics Conf. (AFMC-16), paper D2-4.Google Scholar
Klimenko, A. Y. & Williams, F. A. 2013 On the flame length in firewhirls with strong vorticity. Combust. Flame 160, 335–339.CrossRefGoogle Scholar
Knabb, R. D., Rhome, J. R. & Brown, D. P. 2005 Hurricane Katrina. Tropical Cyclone Report, National Hurricane Center, Florida.Google Scholar
Kuwana, K., Morishita, S., Dobashi, R., Chuah, K. H. & Saito, K. 2011 The burning rate’s effect on the flame length of weak firewhirls. Proc. Combust. Inst. 33, 2425–2432.CrossRefGoogle Scholar
Lee, W. C. & Wurman, J. 2005 Diagnosed three-dimensional axisymmetric structure of the Mulhall Tornado on 3 May 1999. J. Atmos. Sci. 62, 2373–2393.Google Scholar
Lewellen, W. S. 1962 A solution for three-dimensional vortex flows with strong circulation. J. Fluid Mech. 14, 420–432.CrossRefGoogle Scholar
Lewellen, W. S. 1993 Tornado vortex theory. In Tornado: Its Structure, Dynamics, Prediction and Hazards, Geophysical Monograph, vol. 79, pp. 19–40. American Geophysical Union.Google Scholar
Lighthill, Sir J. 1998 Fluid mechanics of tropical cyclones. Theor. Comput. Fluid Mech. 10, 3–21.Google Scholar
Long, R. R. 1961 A vortex in an infinite viscous fluid. J. Fluid Mech. 11, 611–623.Google Scholar
Lundgren, T. S. 1985 The vortical flow above the drain-hole in a rotating vessel. J. Fluid Mech. 155, 381–412.Google Scholar
Mallen, K. J., Montgomery, M. T. & Wang, B. 2005 Reexamining the near-core radial structure of the tropical cyclone primary circulation: implications for vortex resiliency. J. Atmos. Sci. 62, 408–425.Google Scholar
Miller, B. I. 1964 A study of the filling of hurricane Donna (1960) over land. Mon. Weath. Rev. 22, 389–406.Google Scholar
Palmen, E. & Riehl, H. 1957 Budget of angular momentum and energy in tropical cyclones. J. Meteorol. 15, 150–159.Google Scholar
Pearce, R. 1993 A critical review of progress in tropical cyclone physics including experimentation with numerical models. In Proc. ICSU/WMO Intl Symp. on Tropical Cyclone Disasters, Beijing, China, October 1992, pp. 45–49. Beijing University Publishing House.Google Scholar
Powell, M. D., Annane, B., Fleur, R. S., Murillo, S., Dodge, P., Uhlhorn, E., Gamache, J., Cardone, V., Cox, A., Otero, S. & Carrasco, N. 2010 Reconstruction of hurricane Katrina’s wind fields for storm surge and wave hindcasting. Ocean Engng 37 (1), 26–36.Google Scholar
Riehl, H. 1963 Some relationships between wind and thermal structure in steady state hurricanes. J. Atmos. Sci. 20, 276–287.Google Scholar
Rojas, E. S. 2002 Sobre el fenomeno de la autorrotacion. PhD thesis, University of Malaga, Spain.Google Scholar
Shiraishi, M. & Sato, T. 1994 Switching phenomenon of a bathtub vortex. J. Appl. Mech. 61, 850–854.CrossRefGoogle Scholar
Turner, J. S. 1966 The constraints imposed on tornado-like vortices by the top and bottom boundary conditions. J. Fluid Mech. 25, 377–400.Google Scholar
Turner, J. S. & Lilly, D. K. 1963 The carbonated-water tornado vortex. J. Atmos. Sci. 20, 468–471.Google Scholar
Vanyo, J. P. 1993 Rotating Fluids in Engineering and Science. Butterworth-Heinemann.Google Scholar
Wakimoto, R. M., Murphey, H. V., Dowell, D. C. & Bluestein, H. B. 2003 The Kellerville tornado during VORTEX: damage survey and Doppler radar analyses. Mon. Weath. Rev. 131, 2197–2221.Google Scholar
Williams, F. A. 1982 Urban and wildland fire phenomenology. Prog. Energy Combust. Sci. 8, 317–354.Google Scholar
Wurman, J. 2002 The multiple-vortex structure of a tornado. Weath. Forecast. 17, 473–505.Google Scholar
Wurman, J. & Gill, S. 2000 Finescale radar observations of the Dimmitt, Texas (2 June 1995) tornado. Mon. Weath. Rev. 128, 2135–2164.Google Scholar