Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-30T20:17:39.022Z Has data issue: false hasContentIssue false
  • English
  • Français

Streamwise-varying steady transpiration control in turbulent pipe flow

Published online by Cambridge University Press:  19 May 2016

F. Gómez Open the ORCID record for F. Gómez [Opens in a new window] ,
H. M. Blackburn ,
M. Rudman ,
A. S. Sharma  and
B. J. McKeon
F. Gómez*
Affiliation:
Department of Mechanical and Aerospace Engineering, Monash University, Victoria 3800, Australia
H. M. Blackburn
Affiliation:
Department of Mechanical and Aerospace Engineering, Monash University, Victoria 3800, Australia
M. Rudman
Affiliation:
Department of Mechanical and Aerospace Engineering, Monash University, Victoria 3800, Australia
A. S. Sharma
Affiliation:
Faculty of Engineering and the Environment, University of Southampton, Southampton SO17 1BJ, UK
B. J. McKeon
Affiliation:
Graduate Aerospace Laboratories, California Institute of Technology, Pasadena, CA 91125, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The effect of streamwise-varying steady transpiration on turbulent pipe flow is examined using direct numerical simulation at fixed friction Reynolds number $\mathit{Re}_{{\it\tau}}=314$. The streamwise momentum equation reveals three physical mechanisms caused by transpiration acting in the flow: modification of Reynolds shear stress, steady streaming and generation of non-zero mean streamwise gradients. The influence of these mechanisms has been examined by means of a parameter sweep involving transpiration amplitude and wavelength. The observed trends have permitted identification of wall transpiration configurations able to reduce or increase the overall flow rate $-36.1\,\%$ and 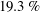$19.3\,\%$, respectively. Energetics associated with these modifications are presented. A novel resolvent formulation has been developed to investigate the dynamics of pipe flows with a constant cross-section but with time-mean spatial periodicity induced by changes in boundary conditions. This formulation, based on a triple decomposition, paves the way for understanding turbulence in such flows using only the mean velocity profile. Resolvent analysis based on the time-mean flow and dynamic mode decomposition based on simulation data snapshots have both been used to obtain a description of the reorganization of the flow structures caused by the transpiration. We show that the pipe flows dynamics are dominated by a critical-layer mechanism and the waviness induced in the flow structures plays a role on the streamwise momentum balance by generating additional terms.

JFM classification

Flow Control: Drag reduction Flow Control: Flow Control Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 796 , 10 June 2016 , pp. 588 - 616
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

del Álamo, J. C. & Jiménez, J. 2006 Linear energy amplification in turbulent channels. J. Fluid Mech. 559, 205–213.CrossRefGoogle Scholar
Bailey, S. C. C. & Smits, A. J. 2010 Experimental investigation of the structure of large- and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 651, 339–356.CrossRefGoogle Scholar
Blackburn, H. M., Hall, P. & Sherwin, S. J. 2013 Lower branch equilibria in Couette flow: the emergence of canonical states for arbitrary shear flows. J. Fluid Mech. 726, 58–85.CrossRefGoogle Scholar
Blackburn, H. M., Ooi, A. S. H. & Chong, M. S. 2007 The effect of corrugation height on flow in a wavy-walled pipe. In 16th Australasian Fluid Mechanics Conference, pp. 559–574. The University of Queensland.Google Scholar
Blackburn, H. M. & Sherwin, S. J. 2004 Formulation of a Galerkin spectral element – Fourier method for three-dimensional incompressible flows in cylindrical geometries. J. Comput. Phys. 197 (2), 759–778.Google Scholar
Blasius, H. 1913 The Law of Similarity of Frictional Processes in Fluids (originally in German). p. 131. Forsch Arbeit Ingenieur-Wesen.Google Scholar
Chen, K. K., Tu, J. H. & Rowley, C. W. 2012 Variants of dynamic mode decomposition: boundary condition, Koopman, and Fourier analyses. J. Nonlinear Sci. 22 (6), 887–915.Google Scholar
Chin, C., Ooi, A. S. H., Marusic, I. & Blackburn, H. M. 2010 The influence of pipe length on turbulence statistics computed from direct numerical simulation data. J. Fluid Mech. 22 (11), 115107.Google Scholar
Choi, H., Moin, P. & Kim, J. 1994 Active turbulence control for drag reduction in wall-bounded flows. J. Fluid Mech. 262, 75–110.Google Scholar
Fukagata, K., Iwamoto, K. & Kasagi, N. 2002 Contribution of Reynolds stress distribution to the skin friction in wall-bounded flows. Phys. Fluids 14 (11), L73–L76.Google Scholar
Gómez, F., Blackburn, H. M., Rudman, M., Mckeon, B. J., Luhar, M., Moarref, R. & Sharma, A. S. 2014 On the origin of frequency sparsity in direct numerical simulations of turbulent pipe flow. Phys. Fluids 26 (10), 101703.Google Scholar
Gómez, F., Blackburn, H. M., Rudman, M., Mckeon, B. J. & Sharma, A. S. 2015 On the coupling of direct numerical simulation and resolvent analysis. In Progress in Turbulence VI: Proceedings of the iTi Conference in Turbulence, Springer.Google Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.Google Scholar
Hama, F. R. 1954 Boundary-layer characteristics for smooth and rough surfaces. Trans. Soc. Nav. Archit. Mar. Engrs 62, 333–358.Google Scholar
Hellström, L. H. O., Sinha, A. & Smits, A. J. 2011 Visualizing the very-large-scale motions in turbulent pipe flow. Phys. Fluids 23 (1), 011703.CrossRefGoogle Scholar
Hellström, L. H. O. & Smits, A. J. 2014 The energetic motions in turbulent pipe flow. Phys. Fluids 26 (12), 125102.Google Scholar
Hoepffner, J. & Fukagata, K. 2009 Pumping or drag reduction? J. Fluid Mech. 635, 171–187.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.Google Scholar
Jimenez, J., Uhlmann, M., Pinelli, A. & Kawahara, G. 2001 Turbulent shear flow over active and passive porous surfaces. J. Fluid Mech. 442, 89–117.Google Scholar
Karniadakis, G. E., Israeli, M. & Orszag, S. A. 1991 High-order splitting methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 97 (2), 414–443.Google Scholar
Kasagi, N., Hasegawa, Y. & Fukagata, K. 2009 Toward cost-effective control of wall turbulence for skin friction drag reduction. In Advances in Turbulence XII, pp. 189–200. Springer.Google Scholar
Kim, J. 2011 Physics and control of wall turbulence for drag reduction. Phil. Trans. R. Soc. Lond. A 369 (1940), 1396–1411.Google ScholarPubMed
Kim, J. & Bewley, T. R. 2007 A linear systems approach to flow control. Annu. Rev. Fluid Mech. 39 (1), 383–417.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.Google Scholar
Luchini, P. 2008 Acoustic streaming and lower-than-laminar drag in controlled channel flow. In Progress in Industrial Mathematics at ECMI 2006, pp. 169–177. Springer.CrossRefGoogle Scholar
Luhar, M., Sharma, A. S. & Mckeon, B. J. 2014 Opposition control within the resolvent analysis framework. J. Fluid Mech. 749, 597–626.Google Scholar
Mao, X., Blackburn, H. M. & Sherwin, S. J. 2015 Nonlinear optimal suppression of vortex shedding from a circular cylinder. J. Fluid Mech. 775, 241–265.CrossRefGoogle Scholar
Marusic, I., Joseph, D. D. & Mahesh, K. 2007 Laminar and turbulent comparisons for channel flow and flow control. J. Fluid Mech. 570, 467–477.Google Scholar
Mckeon, B. J. & Sharma, A. S. 2010 A critical layer framework for turbulent pipe flow. J. Fluid Mech. 658, 336–382.Google Scholar
Mckeon, B. J., Sharma, A. S. & Jacobi, I. 2013 Experimental manipulation of wall turbulence: a systems approach. Phys. Fluids 25 (3), 031301.Google Scholar
Meseguer, A. & Trefethen, L. N. 2003 Linearized pipe flow to Reynolds number 107 . J. Comput. Phys. 186 (1), 178–197.Google Scholar
Mezić, I. 2013 Analysis of fluid flows via spectral properties of the Koopman operator. Annu. Rev. Fluid Mech. 45, 357–378.Google Scholar
Min, T., Kang, S. M., Speyer, J. L. & Kim, J. 2006 Sustained sub-laminar drag in a fully developed channel flow. J. Fluid Mech. 558, 309–318.CrossRefGoogle Scholar
Monty, J. P., Stewart, J. A., Williams, R. C. & Chong, M. S. 2007 Large-scale features in turbulent pipe and channel flows. J. Fluid Mech. 589, 147–156.Google Scholar
Quadrio, M. 2011 Drag reduction in turbulent boundary layers by in-plane wall motion. Phil. Trans. R. Soc. Lond. A 369 (1940), 1428–1442.Google Scholar
Quadrio, M., Floryan, J. M. & Luchini, P. 2007 Effect of streamwise-periodic wall transpiration on turbulent friction drag. J. Fluid Mech. 576, 425–444.Google Scholar
Quadrio, M. & Ricco, P. 2004 Critical assessment of turbulent drag reduction through spanwise wall oscillations. J. Fluid Mech. 521, 251–271.CrossRefGoogle Scholar
Rowley, C. W., Mezić, I., Bagheri, S., Schlatter, P. & Henningson, D. S. 2009 Spectral analysis of nonlinear flows. J. Fluid Mech. 641, 115–127.Google Scholar
Saha, S., Chin, C., Blackburn, H. M. & Ooi, A. S. H. 2011 The influence of pipe length on thermal statistics computed from DNS of turbulent heat transfer. Intl J. Heat Fluid Flow 32 (6), 1083–1097.Google Scholar
Saha, S., Klewicki, J. C., Ooi, A. S. H. & Blackburn, H. M. 2015a Comparison of thermal scaling properties between turbulent pipe and channel flows via DNS. Intl J. Therm. Sci. 89, 43–57.CrossRefGoogle Scholar
Saha, S., Klewicki, J. C., Ooi, A. S. H. & Blackburn, H. M. 2015b Scaling properties of pipe flows with sinusoidal transversely-corrugated walls. J. Fluid Mech. 779, 245–274.Google Scholar
Saha, S., Klewicki, J. C., Ooi, A. S. H., Blackburn, H. M. & Wei, T. 2014 Scaling properties of the equation for passive scalar transport in wall-bounded turbulent flows. Intl J. Heat Mass Transfer 70, 779–792.Google Scholar
Schmid, P. J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39 (1), 129–162.Google Scholar
Schmid, P. J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.Google Scholar
Sharma, A. S. & Mckeon, B. J. 2013 On coherent structure in wall turbulence. J. Fluid Mech. 728, 196–238.Google Scholar
Sharma, A. S., Morrison, J. F., Mckeon, B. J., Limebeer, D. J. N., Koberg, W. H. & Sherwin, S. J. 2011 Relaminarisation of Re 𝜏 = 100 channel flow with globally stabilising linear feedback control. Phys. Fluids 23 (12), 125105.Google Scholar
Smits, A. J., Mckeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.CrossRefGoogle Scholar
Spalart, P. R. & Mclean, J. D. 2011 Drag reduction: enticing turbulence, and then an industry. Phil. Trans. R. Soc. Lond. A 369 (1940), 1556–1569.Google Scholar
Sumitani, Y. & Kasagi, N. 1995 Direct numerical simulation of turbulent transport with uniform wall injection and suction. AIAA J. 33 (7), 1220–1228.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
den Toonder, J. M. J. & Nieuwstadt, F. T. M. 1997 Reynolds number effects in a turbulent pipe flow for low to moderate Re. Phys. Fluids 9 (11), 3398–3409.CrossRefGoogle Scholar
Woodcock, J. D., Sader, J. E. & Marusic, I. 2012 Induced flow due to blowing and suction flow control: an analysis of transpiration. J. Fluid Mech. 690, 366–398.CrossRefGoogle Scholar