Article contents
Streamwise vortex breakdown due to the interaction with crossed shock waves
Published online by Cambridge University Press: 23 October 2023
Abstract
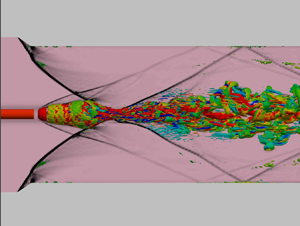
This paper presents a vortex breakdown study due to the interaction between a Batchelor vortex and the crossing of oblique shock waves with Mach numbers of 3.5 and 5.0, favourable for supersonic mixing and combustion, respectively. Numerical simulations were conducted to investigate the effects of the circulation intensity and shock angle on vortex breakdown. The results indicate that a breakdown occurs at the shock angle  $\beta \geqslant 45^\circ$ or the vortex circulation
$\beta \geqslant 45^\circ$ or the vortex circulation  $q = 0.32$, and the configuration is a bubble structure with a recirculation region; most of the breakdowns possess a stagnation point. Furthermore, the structure differs from that of a normal shock wave and vortex interaction because the bubble region is subsonic and does not comprise a normal shock wave on the inside. Additionally, this vortex breakdown shows that the momentum flux on the centreline decreases once at the tip of the bubble owing to a sudden drop in velocity in the subsonic region. In addition, the enstrophy production resulting from vortex stretching and tilting is found to have a significant advantage in the interaction region. Based on these results, the threshold required for a bubble vortex breakdown was theoretically derived as an inequality. The numerical simulation results support the theoretical criterion obtained from the proposed inequality. Therefore, a streamwise vortex breakdown resulting from the interaction between the vortex and intersecting oblique-shocks should be reasonably predicted.
$q = 0.32$, and the configuration is a bubble structure with a recirculation region; most of the breakdowns possess a stagnation point. Furthermore, the structure differs from that of a normal shock wave and vortex interaction because the bubble region is subsonic and does not comprise a normal shock wave on the inside. Additionally, this vortex breakdown shows that the momentum flux on the centreline decreases once at the tip of the bubble owing to a sudden drop in velocity in the subsonic region. In addition, the enstrophy production resulting from vortex stretching and tilting is found to have a significant advantage in the interaction region. Based on these results, the threshold required for a bubble vortex breakdown was theoretically derived as an inequality. The numerical simulation results support the theoretical criterion obtained from the proposed inequality. Therefore, a streamwise vortex breakdown resulting from the interaction between the vortex and intersecting oblique-shocks should be reasonably predicted.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 3
- Cited by



