Article contents
Streamwise variation of turbulent dynamics in boundary layer flow of drag-reducing fluid
Published online by Cambridge University Press: 22 September 2011
Abstract
Direct numerical simulations (DNSs) of a zero-pressure-gradient boundary layer flow of a polymeric fluid have been performed. The FENE-P model was used for the polymer stresses and a wide range of Weissenberg numbers (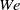 ) was addressed. In all cases, the streamwise variations of the level of polymer stretching and the level of drag reduction are anticorrelated. Consistent with earlier studies, the inlet condition for the flow consists of Newtonian velocity data with no polymer stretching, so in the upstream region of the boundary layer the polymer molecules stretch strongly in response, leading to an initial spatial maximum in polymer stretching. Beyond this initial region, the level of drag reduction increases with increasing downstream position, while the polymer stretch is decreasing. At sufficiently high Weissenberg numbers, these variations are monotonic with streamwise position (outside the upstream region), but at
) was addressed. In all cases, the streamwise variations of the level of polymer stretching and the level of drag reduction are anticorrelated. Consistent with earlier studies, the inlet condition for the flow consists of Newtonian velocity data with no polymer stretching, so in the upstream region of the boundary layer the polymer molecules stretch strongly in response, leading to an initial spatial maximum in polymer stretching. Beyond this initial region, the level of drag reduction increases with increasing downstream position, while the polymer stretch is decreasing. At sufficiently high Weissenberg numbers, these variations are monotonic with streamwise position (outside the upstream region), but at 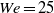 , both the polymer stretching and level of drag reduction display a decaying oscillation in the downstream position. The streamwise dependence of the velocity statistics is also shown. In addition, simulations in which the polymer stress is turned off beyond a chosen downstream position were performed; in this case the flow continues to exhibit substantial drag reduction well downstream of the cutoff position. These observations are analysed in light of other recent literature and in particular the observations of ‘active’ and ‘hibernating’ turbulence recently found in minimal channel flow by Xi and Graham. All of these observations suggest that an important role for viscoelasticity in the turbulent drag reduction phenomenon, at least near solid surfaces, is to suppress conventional turbulence, while leaving behind a much weaker form of turbulence that can persist for a substantial length of time (or downstream distance) even in the absence of viscoelastic stresses.
, both the polymer stretching and level of drag reduction display a decaying oscillation in the downstream position. The streamwise dependence of the velocity statistics is also shown. In addition, simulations in which the polymer stress is turned off beyond a chosen downstream position were performed; in this case the flow continues to exhibit substantial drag reduction well downstream of the cutoff position. These observations are analysed in light of other recent literature and in particular the observations of ‘active’ and ‘hibernating’ turbulence recently found in minimal channel flow by Xi and Graham. All of these observations suggest that an important role for viscoelasticity in the turbulent drag reduction phenomenon, at least near solid surfaces, is to suppress conventional turbulence, while leaving behind a much weaker form of turbulence that can persist for a substantial length of time (or downstream distance) even in the absence of viscoelastic stresses.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2011
References
- 30
- Cited by


