Article contents
Streamwise dispersion of soluble matter in solvent flowing through a tube
Published online by Cambridge University Press: 02 February 2024
Abstract
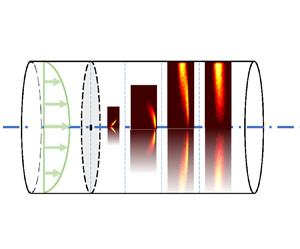
For the dispersion of soluble matter in solvent flowing through a tube as investigated originally by G.I. Taylor, a streamwise dispersion theory is developed from a Lagrangian perspective for the whole process with multi-scale effects. By means of a convected coordinate system to decouple convection from diffusion, a diffusion-type governing equation is presented to reflect superposable diffusion processes with a multi-scale time-dependent anisotropic diffusivity tensor. A short-time benchmark, complementing the existing Taylor–Aris solution, is obtained to reveal novel statistical and physical features of mean concentration for an initial phase with isotropic molecular diffusion. For long times, effective streamwise diffusion prevails asymptotically corresponding to the overall enhanced diffusion in Taylor's classical theory. By inverse integral expansions of local concentration moments, a general streamwise dispersion model is devised to match the short- and long-time asymptotic solutions. Analytical solutions are provided for most typical cases of point and area sources in a Poiseuille tube flow, predicting persistent long tails and skewed platforms. The theoretical findings are substantiated through Monte Carlo simulations, from the initial release to the Taylor dispersion regime. Asymmetries of concentration distribution in a circular tube are certified as originated from (a) initial non-uniformity, (b) unidirectional flow convection, and (c) non-penetration boundary effect. Peculiar peaks in the concentration cloud, enhanced streamwise dispersivity and asymmetric collective phenomena of concentration distributions are illustrated heuristically and characterised to depict the non-equilibrium dispersion. The streamwise perspective could advance our understanding of macro-transport processes of both passive solutes and active suspensions.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
- 7
- Cited by



