Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-08T16:27:37.372Z Has data issue: false hasContentIssue false
  • English
  • Français

Streak instability in turbulent channel flow: the seeding mechanism of large-scale motions

Published online by Cambridge University Press:  26 October 2017

Matteo de Giovanetti Open the ORCID record for Matteo de Giovanetti [Opens in a new window] ,
Hyung Jin Sung Open the ORCID record for Hyung Jin Sung [Opens in a new window]  and
Yongyun Hwang Open the ORCID record for Yongyun Hwang [Opens in a new window]
Matteo de Giovanetti*
Affiliation:
Department of Aeronautics, Imperial College London, South Kensington, London SW7 2AZ, UK
Hyung Jin Sung
Affiliation:
Department of Mechanical Engineering, KAIST, 291 Daehak-ro, Yuseong-gu, Daejeon 34141, South Korea
Yongyun Hwang
Affiliation:
Department of Aeronautics, Imperial College London, South Kensington, London SW7 2AZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

It has often been proposed that the formation of large-scale motion (or bulges) is a consequence of successive mergers and/or growth of near-wall hairpin vortices. In the present study, we report our direct observation that large-scale motion is generated by an instability of an ‘amplified’ streaky motion in the outer region (i.e. very-large-scale motion). 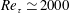We design a numerical experiment in turbulent channel flow up to $Re_{\unicode[STIX]{x1D70F}}\simeq 2000$ where a streamwise-uniform streaky motion is artificially driven by body forcing in the outer region computed from the previous linear theory (Hwang & Cossu, J. Fluid Mech., vol. 664, 2015, pp. 51–73). As the forcing amplitude is increased, it is found that an energetic streamwise vortical structure emerges at a streamwise wavelength of 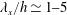$\unicode[STIX]{x1D706}_{x}/h\simeq 1{-}5$ (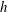$h$ is the half-height of the channel). The application of dynamic mode decomposition and the examination of turbulence statistics reveal that this structure is a consequence of the sinuous-mode instability of the streak, a subprocess of the self-sustaining mechanism of the large-scale outer structures. It is also found that the statistical features of the vortical structure are remarkably similar to those of the large-scale motion in the outer region. Finally, it is proposed that the largest streamwise length of the streak instability determines the streamwise length scale of very-large-scale motion.

JFM classification

Instability: Instability Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulence simulation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 832 , 10 December 2017 , pp. 483 - 513
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19 (4), 041301.Google Scholar
Adrian, R. J., Balachandar, S. & Liu, Z. C. 2001 Spanwise growth of vortex structure in wall turbulence. KSME Intl J. 15 (12), 1741–1749.Google Scholar
del Álamo, J. C. & Jiménez, J. 2003 Spectra of the very large anisotropic scales in turbulent channels. Phys. Fluids 15 (6), 41–44.Google Scholar
del Álamo, J. C. & Jiménez, J. 2006 Linear energy amplification in turbulent channels. J. Fluid Mech. 559, 205–213.Google Scholar
del Álamo, J. C. & Jiménez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5–26.Google Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2006 Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 561, 329–358.Google Scholar
Alizard, F. 2015 Linear stability of optimal streaks in the log-layer of turbulent channel flows. Phys. Fluids 27 (10), 105103.Google Scholar
Andersson, P., Brandt, L., Bottaro, A. & Henningson, D. S. 2001 On the breakdown of boundary layer streaks. J. Fluid Mech. 428, 29–60.CrossRefGoogle Scholar
Baltzer, J. R., Adrian, R. J. & Wu, X. 2013 Structural organization of large and very-large scales in turbulent pipe flow simulation. J. Fluid Mech. 720, 236–279.Google Scholar
Blackwelder, R. F. & Eckelmann, H. 1979 Streamwise vortices associated with the bursting phenomenon. J. Fluid Mech. 94, 577–594.Google Scholar
Butler, K. M. & Farrell, B. F. 1993 Optimal perturbations and streak spacing in wall-bounded turbulent shear flow. Phys. Fluids 3 (5), 774–777.Google Scholar
Canton, J., Örlü, R., Chin, C. & Schlatter, P. 2016 Reynolds number dependence of large-scale friction control in turbulent channel flow. Phys. Rev. Fluids 1 (8), 081501.Google Scholar
Cassinelli, A., de Giovanetti, M. & Hwang, Y. 2017 Streak instability in near-wall turbulence revisited. J. Turbul. 18 (5), 443–464.Google Scholar
Chernyshenko, S. I. & Baig, M. F. 2005 The mechanism of streak formation in near-wall turbulence. J. Fluid Mech. 544, 99–131.Google Scholar
Cossu, C., Pujals, G. & Depardon, S. 2009 Optimal transient growth and very-large-scale structures in turbulent boundary layers. J. Fluid Mech. 619, 79–94.Google Scholar
Flores, O. & Jiménez, J. 2006 Effect of wall-boundary disturbances on turbulent channel flows. J. Fluid Mech. 566, 357–376.Google Scholar
Flores, O. & Jiménez, J. 2010 Hierarchy of minimal flow units in the logarithmic layer. Phys. Fluids 22 (7), 1–4.Google Scholar
de Giovanetti, M., Hwang, Y. & Choi, H. 2016 Skin-friction generation by attached eddies in turbulent channel flow. J. Fluid Mech. 808, 511–538.Google Scholar
Hamilton, J. M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.Google Scholar
Hellström, L. H. O., Marusic, I. & Smits, A. J. 2016 Self-similarity of the large-scale motions in turbulent pipe flow. J. Fluid Mech. 792, R1 1–12.Google Scholar
Hoepffner, J., Brandt, L. & Henningson, D. S. 2005 Transient growth on boundary layer streaks. J. Fluid Mech. 537, 91–100.Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to Re 𝜏 = 2003. Phys. Fluids 18, 1–4.Google Scholar
Hutchins, N. & Marusic, I. 2007 Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365 (1852), 647–664.Google Scholar
Hwang, Y. 2013 Near-wall turbulent fluctuations in the absence of wide outer motions. J. Fluid Mech. 723, 264–288.Google Scholar
Hwang, Y. 2015 Statistical structure of self-sustaining attached eddies in turbulent channel flow. J. Fluid Mech. 767, 254–289.Google Scholar
Hwang, Y. 2016 Mesolayer of attached eddies in turbulent channel flows. Phys. Rev. Fluids 1, 064401.Google Scholar
Hwang, Y. & Bengana, Y. 2016 Self-sustaining process of minimal attached eddies in turbulent channel flow. J. Fluid Mech. 795, 708–738.Google Scholar
Hwang, Y. & Cossu, C. 2010a Amplification of coherent streaks in the turbulent Couette flow: an input–output analysis at low Reynolds number. J. Fluid Mech. 643, 333–348.Google Scholar
Hwang, Y. & Cossu, C. 2010b Linear non-normal energy amplification of harmonic and stochastic forcing in the turbulent channel flow. J. Fluid Mech. 664, 51–73.Google Scholar
Hwang, Y. & Cossu, C. 2010c Self-sustained process at large scales in turbulent channel flow. Phys. Rev. Lett. 105 (4), 1–10.Google Scholar
Hwang, Y. & Cossu, C. 2011 Self-sustained processes in the logarithmic layer of turbulent channel flows. Phys. Fluids 23 (6), 061702.Google Scholar
Hwang, Y., Willis, A. P. & Cossu, C. 2016 Invariant solutions of minimal large-scale structures in turbulent channel flow for Re up to 1000. J. Fluid Mech. 802, R1.Google Scholar
Jeong, J. & Hussain, F. 1997 Coherent structures near the wall in a turbulent channel flow. J. Fluid Mech. 332, 185–214.Google Scholar
Jiménez, J. 2013a How linear is wall-bounded turbulence? Phys. Fluids 25 (11), 110814.Google Scholar
Jiménez, J. 2013b Near-wall turbulence. Phys. Fluids 25 (10), 101302.Google Scholar
Jiménez, J. & Hoyas, S. 2008 Turbulent fluctuations above the buffer layer of wall-bounded flows. J. Fluid Mech. 611, 215–236.Google Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.Google Scholar
Jovanović, M. R., Schmid, P. J. & Nichols, J. W. 2014 Sparsity-promoting dynamic mode decomposition. Phys. Fluids 26 (2), 1–22.Google Scholar
Kim, H. T., Kline, S. J. & Reynolds, W. C. 1971 The production of turbulence near a smooth wall in a turbulent boundary layer. J. Fluid Mech. 50 (1), 133–160.Google Scholar
Kim, J. 2011 Physics and control of wall turbulence for drag reduction. Phil. Trans. R. Soc. Lond. A 369 (1940), 1396–1411.Google Scholar
Kim, J., Moin, P. & Moser, R. D. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.Google Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Rundstatler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30, 741–773.Google Scholar
Kovasznay, L. S. G. 1970 The turbulent boundary layer. Annu. Rev. Fluid Mech. 2, 95–112.Google Scholar
Landahl, M. T. 1980 A note on an algebraic instability of inviscid parallel shear flows. J. Comput. Phys. 98, 243–251.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3 1–11.Google Scholar
Monty, J. P., Hutchins, N., Ng, H. C. H., Marusic, I. & Chong, M. S. 2009 A comparison of turbulent pipe, channel and boundary layer flows. J. Fluid Mech. 632, 431–442.Google Scholar
Nickels, T. B., Marusic, I., Hafez, S. & Chong, M. S. 2005 Evidence of the k 1 -1 law in a high-Reynolds-number turbulent boundary layer. Phys. Rev. Lett. 95 (7), 1–4.CrossRefGoogle Scholar
Park, D. S. & Huerre, P. 1995 Primary and secondary instabilities of the asymptotic suction boundary layer on a curved plate. J. Fluid Mech. 283, 249–272.Google Scholar
Park, J., Hwang, Y. & Cossu, C. 2011 On the stability of large-scale streaks in turbulent Couette and Poiseulle flows. C. R. Méc. 339 (1), 1–5.Google Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.Google Scholar
Perry, A. E., Henbest, S. & Chong, M. S. 1986 Theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.CrossRefGoogle Scholar
Perry, A. E. & Marusic, I. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 1. Extension of the attached eddy hypothesis. J. Fluid Mech. 298, 389–407.Google Scholar
Pujals, G., García-Villalba, M., Cossu, C. & Depardon, S. 2009 A note on optimal transient growth in turbulent channel flows. Phys. Fluids 21 (1), 1–6.Google Scholar
Reynolds, W. C. & Hussain, A. K. M. F. 1972 The mechanics of an organized wave in turbulent shear flow. Part 3. Theoretical models and comparisons with experiments. J. Fluid Mech. 54 (2), 263–288.Google Scholar
Reynolds, W. C. & Tiederman, W. G. 1967 Stability of turbulent channel flow, with application to Malkus’s theory. J. Fluid Mech. 27 (2), 253–272.Google Scholar
Schmid, P. J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.Google Scholar
Schoppa, W. & Hussain, F. 1998 Genesis of longitudinal vortices in near-wall turbulence. Meccanica 33 (5), 489–501.Google Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.Google Scholar
Sharma, A. S. & McKeon, B. J. 2013 On coherent structure in wall turbulence. J. Fluid Mech. 728, 196–238.Google Scholar
Smith, C. R. & Metzler, S. P. 1983 The characteristics of low-speed streaks in the near-wall region of a turbulent boundary layer. J. Fluid Mech. 129, 27–54.Google Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.Google Scholar
Townsend, A. A. 1961 Equilibrium layers and wall turbulence. J. Fluid Mech. 12, 97–120.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 1st edn. Cambridge University Press.Google Scholar
Vreman, A. W. 2004 An eddy-viscosity subgrid-scale model for turbulent shear flow: algebraic theory and applications. Phys. Fluids 16 (10), 3670–3681.Google Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9 (4), 883–900.Google Scholar
Willis, A. P., Hwang, Y. & Cossu, C. 2010 Optimally amplified large-scale streaks and drag reduction in turbulent pipe flow. Phys. Rev. E 82 (3), 1–11.Google Scholar
Zare, A., Jovanović, M. R. & Georgiou, T. 2017 Colour of turbulence. J. Fluid Mech. 812, 636–680.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar