Article contents
Stratified wake of a tilted cylinder. Part 2. Lee internal waves
Published online by Cambridge University Press: 17 April 2012
Abstract
This experimental, numerical and theoretical study considers the lee internal waves generated by the wake of a circular cylinder, whose axis is tilted with respect to a stable density gradient. The main difference with the case of a horizontal cylinder is that the lee waves contain a large axial velocity, which are located in a row of lobes extending downstream from the cylinder. At small tilt angles, the wavelength is equal to 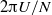 ,
, 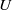 being the velocity of the cylinder and
being the velocity of the cylinder and 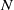 the Brunt–Väisälä frequency, which can be explained by the fact that the group velocity of the waves is small. The amplitude of the waves can be predicted using the Lighthill theory for dispersive waves applied to the case of a tilted bluff body. The flow around the cylinder is modelled empirically in order to reach a quantitative prediction in good agreement with the experimental and numerical results. The spatial structure of the predicted internal waves is qualitatively correct although some discrepancies arise because the advection by the flow around the cylinder is neglected.
the Brunt–Väisälä frequency, which can be explained by the fact that the group velocity of the waves is small. The amplitude of the waves can be predicted using the Lighthill theory for dispersive waves applied to the case of a tilted bluff body. The flow around the cylinder is modelled empirically in order to reach a quantitative prediction in good agreement with the experimental and numerical results. The spatial structure of the predicted internal waves is qualitatively correct although some discrepancies arise because the advection by the flow around the cylinder is neglected.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 8
- Cited by


