Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-24T14:27:10.868Z Has data issue: false hasContentIssue false
  • English
  • Français

Stokes flow near the contact line of an evaporating drop

Published online by Cambridge University Press:  31 August 2012

Hanneke Gelderblom ,
Oscar Bloemen  and
Jacco H. Snoeijer
Hanneke Gelderblom*
Affiliation:
Physics of Fluids Group, Faculty of Science and Technology, Mesa+ Institute, University of Twente, 7500 AE Enschede, The Netherlands
Oscar Bloemen
Affiliation:
Physics of Fluids Group, Faculty of Science and Technology, Mesa+ Institute, University of Twente, 7500 AE Enschede, The Netherlands
Jacco H. Snoeijer
Affiliation:
Physics of Fluids Group, Faculty of Science and Technology, Mesa+ Institute, University of Twente, 7500 AE Enschede, The Netherlands
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

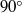The evaporation of sessile drops in quiescent air is usually governed by vapour diffusion. For contact angles below , the evaporative flux from the droplet tends to diverge in the vicinity of the contact line. Therefore, the description of the flow inside an evaporating drop has remained a challenge. Here, we focus on the asymptotic behaviour near the pinned contact line, by analytically solving the Stokes equations in a wedge geometry of arbitrary contact angle. The flow field is described by similarity solutions, with exponents that match the singular boundary condition due to evaporation. We demonstrate that there are three contributions to the flow in a wedge: the evaporative flux, the downward motion of the liquid–air interface and the eigenmode solution which fulfils the homogeneous boundary conditions. Below a critical contact angle of 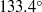, the evaporative flux solution will dominate, while above this angle the eigenmode solution dominates. We demonstrate that for small contact angles, the velocity field is very accurately described by the lubrication approximation. For larger contact angles, the flow separates into regions where the flow is reversing towards the drop centre.

JFM classification

Interfacial Flows (free surface): Capillary flows Interfacial Flows (free surface): Contact lines Drops and Bubbles: Drops
Type
Papers
Information
Journal of Fluid Mechanics , Volume 709 , 25 October 2012 , pp. 69 - 84
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Anderson, D. & Davis, S. 1995 The spreading of volatile liquid droplets on heated surfaces. Phys. Fluids 7 (2), 248–265.CrossRefGoogle Scholar
2. Berteloot, G., Pham, C. T., Daerr, A., Lequeux, F. & Limat, L. 2008 Evaporation-induced flow near a contact line: consequences on coating and contact angle. Europhys. Lett. 83, 14003.CrossRefGoogle Scholar
3. Bigioni, T. P., Lin, X. M., Nguyen, T. T., Corwin, E. I., Witten, T. A. & Jaeger, H. M. 2006 Kinetically driven self assembly of highly ordered nanoparticle monolayers. Nature Mater. 5 (4), 265–270.CrossRefGoogle ScholarPubMed
4. Bodiguel, H. & Leng, J. 2010 Imaging the drying of a colloidal suspension. Soft Matt. 6 (21), 5451–5460.CrossRefGoogle Scholar
5. Brutin, D., Sobac, B., Loquet, B. & Sampol, J. 2011 Pattern formation in drying drops of blood. J. Fluid Mech. 667, 85–95.CrossRefGoogle Scholar
6. Burelbach, J. P., Bankoff, S. G. & Davis, S. H. 1988 Nonlinear stability of evaporating condensing liquid films. J. Fluid Mech. 195, 463–494.CrossRefGoogle Scholar
7. Cazabat, A. M. & Guéna, G. 2010 Evaporation of macroscopic sessile droplets. Soft Matt. 6 (12), 2591–2612.CrossRefGoogle Scholar
8. Colinet, P. & Rednikov, A. 2011 On integrable singularities and apparent contact angles within a classical paradigm. Eur. Phys. J. Spec. Top. 197 (1), 89–113.CrossRefGoogle Scholar
9. Dean, W. R. & Montagnon, P. E. 1949 On the steady motion of viscous liquid in a corner. Proc. Camb. Phil. Soc. 45, 389–394.CrossRefGoogle Scholar
10. Deegan, R. D., Bakajin, O., Dupont, T. F., Huber, G., Nagel, S. R. & Witten, T. A. 1997 Capillary flow as the cause of ring stains from dried liquid drops. Nature 389 (6653), 827–828.CrossRefGoogle Scholar
11. Deegan, R. D., Bakajin, O., Dupont, T. F., Huber, G., Nagel, S. R. & Witten, T. A. 2000 Contact line deposits in an evaporating drop. Phys. Rev. E 62 (1), 756–765.CrossRefGoogle Scholar
12. Dufresne, E. R., Corwin, E. I., Greenblatt, N. A., Ashmore, J., Wang, D. Y., Dinsmore, A. D., Cheng, J. X., Xie, X. S., Hutchinson, J. W. & Weitz, D. A. 2003 Flow and fracture in drying nanoparticle suspensions. Phys. Rev. Lett. 91 (22), 224501.CrossRefGoogle ScholarPubMed
13. Eggers, J. & Pismen, L. M. 2010 Non-local description of evaporating drops. Phys. Fluids 22 (11), 112101.CrossRefGoogle Scholar
14. Eral, H. B., Augustine, D. M., Duits, M. H. G. & Mugele, F. 2011 Suppressing the coffee stain effect: how to control colloidal self-assembly in evaporating drops using electrowetting. Soft Matt. 7, 1–5.CrossRefGoogle Scholar
15. Fischer, B. J. 2002 Particle convection in an evaporating colloidal droplet. Langmuir 18, 60–67.CrossRefGoogle Scholar
16. Gelderblom, H., Marín, A. G., Nair, H., van Housselt, A., Lefferts, L., Snoeijer, J. H. & Lohse, D. 2011 How water droplets evaporate on a superhydrophobic substrate. Phys. Rev. E 83 (2), 026306.CrossRefGoogle ScholarPubMed
17. Guéna, G., Poulard, C. & Cazabat, A. M. 2007 The leading edge of evaporating droplets. J. Colloid Interface Sci. 312 (1), 164–171.CrossRefGoogle Scholar
18. Haut, B. & Colinet, P. 2005 Surface-tension-driven instabilities of a pure liquid layer evaporating into an inert gas. J. Colloid Interface Sci. 285 (1), 296–305.CrossRefGoogle ScholarPubMed
19. Hu, H. & Larson, R. G. 2002 Evaporation of a sessile droplet on a substrate. J. Phys. Chem. B 106 (6), 1334–1344.CrossRefGoogle Scholar
20. Hu, H. & Larson, R. G. 2005 Analysis of the microfluidic flow in an evaporating sessile droplet. Langmuir 21 (9), 3963–3971.CrossRefGoogle Scholar
21. Hu, H. & Larson, R. G. 2006 Marangoni effect reverses coffee-ring depositions. J. Phys. Chem. B 110 (14), 7090–7094.CrossRefGoogle ScholarPubMed
22. Huh, C. & Scriven, L. E. 1971 Hydrodynamic model of steady movement of a solid/liquid/fluid contact line. J. Colloid Interface Sci. 35 (1), 85–101.CrossRefGoogle Scholar
23. Marín, A. G., Gelderblom, H., Lohse, D. & Snoeijer, J. H. 2011 Order-to-disorder transition in ring-shaped colloidal stains. Phys. Rev. Lett. 107, 085502.CrossRefGoogle ScholarPubMed
24. Masoud, H. & Felske, J. D. 2009 Analytical solution for Stokes flow inside an evaporating drop: spherical and cylindrical cap shapes. Phys. Fluids 21, 042102.CrossRefGoogle Scholar
25. Michell, J. H. 1899 On the direct determination of stress in an elastic solid, with application to the theory of plates. Proc. Lond. Math. Soc. 100 (31), 100–124.CrossRefGoogle Scholar
26. Moffatt, H. K. 1964 Viscous and resistive eddies near a sharp corner. J. Fluid Mech. 18, 1–18.CrossRefGoogle Scholar
27. Moffatt, H. K. & Duffy, B. R. 1980 Local similarity solutions and their limitations. J. Fluid Mech. 96, 299–313.CrossRefGoogle Scholar
28. Murisic, N. & Kondic, L. 2011 On evaporation of sessile drops with moving contact lines. J. Fluid Mech. 679, 219–246.CrossRefGoogle Scholar
29. Petsi, A. J. & Burganos, V. N. 2008 Stokes flow inside an evaporating liquid line for any contact angle. Phys. Rev. E 78, 036324.CrossRefGoogle ScholarPubMed
30. Pham, C. T., Berteloot, G., Lequeux, F. & Limat, L. 2010 Dynamics of complete wetting liquid under evaporation. Europhys. Lett. 92 (5), 54005.CrossRefGoogle Scholar
31. Popov, Y. O. 2005 Evaporative deposition patterns: spatial dimensions of the deposit. Phys. Rev. E 71 (3), 036313.CrossRefGoogle ScholarPubMed
32. Poulard, C., Guena, G., Cazabat, A. M., Boudaoud, A. & Ben Amar, M. 2005 Rescaling the dynamics of evaporating drops. Langmuir 21 (18), 8226–8233.CrossRefGoogle ScholarPubMed
33. Ristenpart, W. D., Kim, P. G., Domingues, C., Wan, J. & Stone, H. A. 2007 Influence of substrate conductivity on circulation reversal in evaporating drops. Phys. Rev. Lett. 99 (23), 234502.CrossRefGoogle ScholarPubMed
34. Semenov, S., Starov, V. M., Velarde, M. G. & Rubio, R. G. 2011 Droplets evaporation: problems and solutions. Eur. Phys. J. Spec. Top. 197 (1), 265–278.CrossRefGoogle Scholar
35. Sobac, B. & Brutin, D. 2011 Triple-line behaviour and wettability controlled by nanocoated substrates: influence on sessile drop evaporation. Langmuir 27 (24), 14999–15007.CrossRefGoogle ScholarPubMed
36. Velikov, K. P. 2002 Layer-by-layer growth of binary colloidal crystals. Science 296 (5565), 106–109.CrossRefGoogle ScholarPubMed
37. Yunker, P. J., Still, T., Lohr, M. A. & Yodh, A. G. 2011 Suppression of the coffee-ring effect by shape-dependent capillary interactions. Nature 476 (7360), 308–311.CrossRefGoogle ScholarPubMed