Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T22:28:05.876Z Has data issue: false hasContentIssue false
  • English
  • Français

Steady detonation propagation in a circular arc: a Detonation Shock Dynamics model

Published online by Cambridge University Press:  18 October 2016

Mark Short ,
James J. Quirk ,
Chad D. Meyer  and
Carlos Chiquete
Mark Short*
Affiliation:
Los Alamos National Laboratory, Los Alamos, NM 87545, USA
James J. Quirk
Affiliation:
Los Alamos National Laboratory, Los Alamos, NM 87545, USA
Chad D. Meyer
Affiliation:
Los Alamos National Laboratory, Los Alamos, NM 87545, USA
Carlos Chiquete
Affiliation:
Los Alamos National Laboratory, Los Alamos, NM 87545, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the physics of steady detonation wave propagation in a two-dimensional circular arc via a Detonation Shock Dynamics (DSD) surface evolution model. The dependence of the surface angular speed and surface spatial structure on the inner arc radius (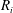$R_{i}$), the arc thickness (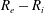$R_{e}-R_{i}$, where 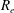$R_{e}$ is the outer arc radius) and the degree of confinement on the inner and outer arc is examined. We first analyse the results for a linear 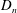$D_{n}$–$\unicode[STIX]{x1D705}$ model, in which the normal surface velocity 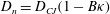$D_{n}=D_{CJ}(1-B\unicode[STIX]{x1D705})$, where 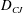$D_{CJ}$ is the planar Chapman–Jouguet velocity, $\unicode[STIX]{x1D705}$ is the total surface curvature and 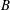$B$ is a length scale representative of a reaction zone thickness. An asymptotic analysis assuming the ratio 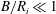$B/R_{i}\ll 1$ is conducted for this model and reveals a complex surface structure as a function of the radial variation from the inner to the outer arc. For sufficiently thin arcs, where $(R_{e}-R_{i})/R_{i}=O(B/R_{i})$, the angular speed of the surface depends on the inner arc radius, the arc thickness and the inner and outer arc confinement. For thicker arcs, where 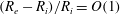$(R_{e}-R_{i})/R_{i}=O(1)$, the angular speed does not depend on the outer arc radius or the outer arc confinement to the order calculated. It is found that the leading-order angular speed depends only on 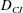$D_{CJ}$ and 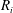$R_{i}$, and corresponds to a Huygens limit (zero curvature) propagation model where 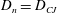$D_{n}=D_{CJ}$, assuming a constant angular speed and perfect confinement on the inner arc surface. Having the normal surface speed depend on curvature requires the insertion of a boundary layer structure near the inner arc surface. This is driven by an increase in the magnitude of the surface wave curvature as the inner arc surface is approached that is needed to meet the confinement condition on the inner arc surface. For weak inner arc confinement, the surface wave spatial variation with the radial coordinate is described by a triple-deck structure. The first-order correction to the angular speed brings in a dependence on the surface curvature through the parameter 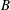$B$, while the influence of the inner arc confinement on the angular velocity only appears in the second-order correction. For stronger inner arc confinement, the surface wave structure is described by a two-layer solution, where the effect of the confinement on the angular speed is promoted to the first-order correction. We also compare the steady-state arc solution for a PBX 9502 DSD model to an experimental two-dimensional arc geometry validation test.

JFM classification

Compressible Flows: Compressible Flows Compressible Flows: Detonation waves Compressible Flows: Shock waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 807 , 25 November 2016 , pp. 87 - 134
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aslam, T. D. & Bdzil, J. B. 2002 Numerical and theoretical investigations on detonation-inert confinement interactions. In Twelfth International Symposium on Detonation, Office of Naval Research ONR 333-05-2, pp. 483–488.Google Scholar
Aslam, T. D. & Bdzil, J. B. 2006 Numerical and theoretical investigations on detonation confinement sandwich tests. In Thirteenth International Detonation Symposium, Office of Naval Research ONR 351-07-01, pp. 761–769.Google Scholar
Aslam, T. D., Bdzil, J. B. & Stewart, D. S. 1996 Level set methods applied to modeling detonation shock dynamics. J. Comput. Phys. 126, 390–409.CrossRefGoogle Scholar
Aslam, T. D. & Short, M.2013 Detonation Shock Dynamics overview and calibration. Tech. Rep. LA-UR-13-26358. Los Alamos National Laboratory.Google Scholar
Aslam, T. D. & Stewart, D. S. 1999 Detonation shock dynamics and comparisons with direct numerical simulation. Combust. Theor. Model. 3, 77–101.Google Scholar
Bdzil, J. B. 1981 Steady-state two-dimensional detonation. J. Fluid Mech. 108, 195–226.CrossRefGoogle Scholar
Bdzil, J. B., Aida, T., Henninger, R. J. & Walter, J. W.2007 Test problems for DSD3D. Tech. Rep. LA-14366. Los Alamos National Laboratory.Google Scholar
Bdzil, J. B., Aslam, T. D., Henninger, R. & Quirk, J. J. 2003 High-explosives performance: understanding the effects of a finite-length reaction zone. Los Alamos Science 28, 96–110.Google Scholar
Bdzil, J. B., Fickett, W. & Stewart, D. S. 1989 Detonation Shock Dynamics: a new approach to modeling multi-dimensional detonation waves. In Ninth Symposium (International) on Detonation, Office of the Chief of Naval Research OCNR 113291-7, pp. 730–742.Google Scholar
Bdzil, J. B., Henninger, R. J. & Walter, J. W.2006 Test problems for DSD2D. Tech. Rep. LA-14277. Los Alamos National Laboratory.Google Scholar
Bdzil, J. B. & Stewart, D. S. 1986 Time-dependent two-dimensional detonation: the interaction of edge rarefactions with finite-length reaction zones. J. Fluid. Mech. 171, 1–26.CrossRefGoogle Scholar
Bdzil, J. B. & Stewart, D. S. 1989 Modelling two-dimensional detonations with detonation shock dynamics. Phys. Fluids A 1, 1261–1267.CrossRefGoogle Scholar
Bdzil, J. B. & Stewart, D. S. 2007 The dynamics of detonation in explosive systems. Annu. Rev. Fluid Mech. 39, 263–292.CrossRefGoogle Scholar
Bdzil, J. B. & Stewart, D. S. 2011 Theory of Detonation Shock Dynamics. In Detonation Dynamics (ed. Zhang, F.), Shock Waves Science and Technology Library, vol. 6, pp. 373–453. Springer.Google Scholar
Fickett, W. & Davis, W. C. 1979 Detonation. University of California Press.Google Scholar
Hernández, A., Bdzil, J. B. & Stewart, D. S. 2013 An MPI parallel level-set algorithm for propagating front curvature dependent detonation shock fronts in complex geometries. Combust. Theor. Model. 17, 109–141.Google Scholar
Hill, L. G. & Aslam, T. D. 2010 Detonation Shock Dynamics calibration for PBX 9502 with temperature, density, and material lot variations. In Fourteenth International Detonation Symposium, Office of Naval Research ONR-351-10-185, pp. 779–788.Google Scholar
Hodgson, A. N. 2014 Modelling an IHE experiment with a suite of DSD models. J. Phys.: Conf. Ser. 500 (5), 052018.Google Scholar
Jackson, S. I. & Short, M. 2015 Scaling of detonation velocity in cylinder and slab geometries for ideal, insensitive and non-ideal explosives. J. Fluid Mech. 773, 224–266.Google Scholar
Kapila, A. K., Bdzil, J. B. & Stewart, D. S. 2006 On the structure and accuracy of programmed burn. Combust. Theor. Model. 10, 289–321.Google Scholar
Lambert, D. E., Stewart, D. S., Yoo, S. & Wescott, B. L. 2006 Experimental validation of detonation shock dynamics in condensed explosives. J. Fluid Mech. 546, 227–253.Google Scholar
Lieberthal, B., Bdzil, J. B. & Stewart, D. S. 2014 Modelling detonation of heterogeneous explosives with embedded inert particles using detonation shock dynamics: normal and divergent propagation in regular and simplified microstructure. Combust. Theor. Model. 18, 204–241.Google Scholar
Lubyatinsky, S. N., Batalov, S. V., Garmashev, A. Yu., Israelyan, V. G., Kostitsyn, O. V., Loboiko, B. G., Pashentsev, V. A., Sibilev, V. A., Smirnov, E. B. & Filin, V. P. 2003 Detonation propagation in 180° ribs of an insensitive high explosive. In Shock Compression of Condensed Matter (ed. Furnish, M. D., Gupta, Y. M. & Forbes, J. W.), pp. 859–862. American Institute of Physics; AIP Conf. Proc. 706.Google Scholar
Meyer, C. D., Quirk, J. J., Short, M. & Chiquete, C.2016 Evaluation of a programmed burn methodology for detonation propagation using Detonation Shock Dynamics and the Pseudo-Reaction-Zone model (submitted).Google Scholar
Nakayama, H., Kasahara, J., Matsuo, A. & Funaki, I. 2013 Front shock behavior of stable curved detonation waves in rectangular-cross-section curved channels. Proc. Combust. Inst. 34, 1939–1947.Google Scholar
Nakayama, H., Moriya, T., Kasahara, J., Matsuo, A., Sasamoto, Y. & Funaki, I. 2012 Stable detonation wave propagation in rectangular-cross-section curved channels. Combust. Flame 159, 859–869.Google Scholar
Stewart, D. S. & Bdzil, J. B. 1988a A lecture on Detonation-Shock Dynamics. In Mathematical Modeling in Combustion Science (ed. Buckmaster, J. D. & Takeno, T.), Lecture Notes in Physics, vol. 299, pp. 17–30. Springer.CrossRefGoogle Scholar
Stewart, D. S. & Bdzil, J. B. 1988b The shock dynamics of stable multidimensional detonation. Combust. Flame 72, 311–323.CrossRefGoogle Scholar
Tarver, C. M. & Chidester, S. K. 2007 Ignition and growth modeling of detonating TATB cones and arcs. In Shock Compression of Condensed Matter (ed. Elert, M., Furnish, M. D., Chau, R., Holmes, N. & Nguyen, J.), pp. 429–432. American Institute of Physics; AIP Conf. Proc. 955.Google Scholar