Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-24T12:58:24.092Z Has data issue: false hasContentIssue false
  • English
  • Français

Steady circular hydraulic jump on a rotating disk

Published online by Cambridge University Press:  28 September 2021

Anna Ipatova Open the ORCID record for Anna Ipatova [Opens in a new window] ,
K.V. Smirnov Open the ORCID record for K.V. Smirnov [Opens in a new window]  and
E.I. Mogilevskiy Open the ORCID record for E.I. Mogilevskiy [Opens in a new window]
Anna Ipatova
Affiliation:
Faculty of Mechanics and Mathematics, Lomonosov Moscow State University, Leninskie gory, 1, 119991 Moscow, Russia Université de Lille, CNRS, IEMN UMR 8520, F-59000 Lille, France
K.V. Smirnov
Affiliation:
Faculty of Mechanics and Mathematics, Lomonosov Moscow State University, Leninskie gory, 1, 119991 Moscow, Russia
E.I. Mogilevskiy*
Affiliation:
Faculty of Mechanics and Mathematics, Lomonosov Moscow State University, Leninskie gory, 1, 119991 Moscow, Russia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

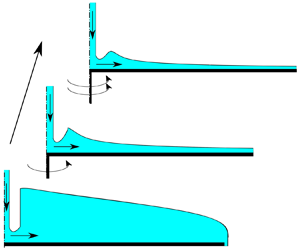
The paper deals with the steady axially symmetric flow of a viscous liquid layer over a rotating disk. The liquid is fed near the axis of rotation and spreads due to inertia and the centrifugal force. The viscous shallow-water approach gives a system of ordinary differential equations governing the flow. We consider inertia, gravity, centrifugal and Coriolis forces and estimate the effect of surface tension. We found four qualitatively different flow regimes. Transition through these regimes shows the continuous evolution of the flow structure from a hydraulic jump on a static disk to a monotonic thickness decrease on a fast rotating one. We show that, in the absence of surface tension, the intensity of the jump gradually vanishes at a finite distance from the axis of rotation while the angular velocity increases. The surface tension decreases the jump radius and destroys the steady solution for a certain range of parameters.

JFM classification

Interfacial Flows (free surface): Thin films Waves/Free-surface Flows: Hydraulics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 927 , 25 November 2021 , A24
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Anderson, J.D. 1995 Computational Fluid Dynamics. Computational Fluid Dynamics: The Basics with Applications. McGraw-Hill Education.Google Scholar
Askarizadeh, H., Ahmadikia, H., Ehrenpreis, C., Kneer, R., Pishevar, A. & Rohlfs, W. 2019 Role of gravity and capillary waves in the origin of circular hydraulic jumps. Phys. Rev. Fluids 4, 114002.CrossRefGoogle Scholar
Avedisian, C.T. & Zhao, Z. 2000 The circular hydraulic jump in low gravity. Proc. R. Soc. Lond. A 456 (2001), 2127–2151.10.1098/rspa.2000.0606CrossRefGoogle Scholar
Batchelor, G.K. 2000 An Introduction to Fluid Dynamics. Cambridge Mathematical Library. Cambridge University Press.10.1017/CBO9780511800955CrossRefGoogle Scholar
Bhagat, R.K., Jha, N.K., Linden, P.F. & Wilson, D.I. 2018 On the origin of the circular hydraulic jump in a thin liquid film. J. Fluid Mech. 851, R5.CrossRefGoogle Scholar
Bhagat, R.K. & Linden, P.F. 2020 The circular capillary jump. J. Fluid Mech. 896, A25.10.1017/jfm.2020.303CrossRefGoogle Scholar
Bohr, T., Dimon, P. & Putkaradze, V. 1993 Shallow-water approach to the circular hydraulic jump. J. Fluid Mech. 254, 635–648.10.1017/S0022112093002289CrossRefGoogle Scholar
Bohr, T. & Scheichl, B. 2021 Surface tension and energy conservation in a moving fluid. Phys. Rev. Fluids 6, L052001.CrossRefGoogle Scholar
Brechet, Y. & Néda, Z. 1999 On the circular hydraulic jump. Am. J. Phys. 67 (8), 723–731.CrossRefGoogle Scholar
Bush, J.W.M. & Aristoff, J.M. 2003 The influence of surface tension on the circular hydraulic jump. J. Fluid Mech. 489, 229–238.CrossRefGoogle Scholar
Bush, J.W.M., Aristoff, J.M. & Hosoi, A.E. 2006 An experimental investigation of the stability of the circular hydraulic jump. J. Fluid Mech. 558, 33–52.CrossRefGoogle Scholar
Charwat, A.F., Kelly, R.E. & Gazley, C. 1972 The flow and stability of thin liquid films on a rotating disk. J. Fluid Mech. 53 (2), 227–255.CrossRefGoogle Scholar
Choo, K. & Kim, S.J. 2016 The influence of nozzle diameter on the circular hydraulic jump of liquid jet impingement. Exp. Therm. Fluid Sci. 72, 12–17.CrossRefGoogle Scholar
Duchesne, A., Andersen, A. & Bohr, T. 2019 Surface tension and the origin of the circular hydraulic jump in a thin liquid film. Phys. Rev. Fluids 4 (8), 084001.CrossRefGoogle Scholar
Duchesne, A., Lebon, L. & Limat, L. 2014 Constant Froude number in a circular hydraulic jump and its implication on the jump radius selection. Europhys. Lett. 107 (5), 54002.CrossRefGoogle Scholar
Ellegaard, C., Hansen, A.E., Haaning, A., Hansen, K., Marcussen, A., Bohr, T., Hansen, J.L. & Watanabe, S. 1998 Creating corners in kitchen sinks. Nature 392 (6678), 767–768.CrossRefGoogle Scholar
Espig, H. & Hoyle, R. 1965 Waves in a thin liquid layer on a rotating disk. J. Fluid Mech. 22 (4), 671–677.10.1017/S0022112065001052CrossRefGoogle Scholar
Fernandez-Feria, R., Sanmiguel-Rojas, E. & Benilov, E.S. 2019 On the origin and structure of a stationary circular hydraulic jump. Phys. Fluids 31 (7), 072104.CrossRefGoogle Scholar
Foglizzo, T., Masset, F., Guilet, J. & Durand, G. 2012 Shallow water analogue of the standing accretion shock instability: experimental demonstration and a two-dimensional model. Phys. Rev. Lett. 108, 051103.CrossRefGoogle Scholar
Hansen, S.H., Hørlück, S., Zauner, D., Dimon, P., Ellegaard, C. & Creagh, S.C. 1997 Geometric orbits of surface waves from a circular hydraulic jump. Phys. Rev. E 55, 7048–7062.CrossRefGoogle Scholar
Ivanova, K.A. & Gavrilyuk, S.L. 2019 Structure of the hydraulic jump in convergent radial flows. J. Fluid Mech. 860, 441–464.CrossRefGoogle Scholar
Jannes, G., Piquet, R., Maïssa, P., Mathis, C. & Rousseaux, G. 2011 Experimental demonstration of the supersonic-subsonic bifurcation in the circular jump: a hydrodynamic white hole. Phys. Rev. E 83, 056312.CrossRefGoogle ScholarPubMed
Kalliadasis, S., Ruyer-Quil, C., Scheid, B. & Velarde, M.G. 2011 Falling Liquid Films. Applied Mathematical Sciences. Springer.Google Scholar
Kapitza, P.L. & Kapitza, S.P. 1949 Wavy flow of thin layers of a viscous fluid. Zh. Eksp. Teor. Fiz. 19, 105–120.Google Scholar
Kasimov, A.R. 2008 A stationary circular hydraulic jump, the limits of its existence and its gasdynamic analogue. J. Fluid Mech. 601, 189–198.CrossRefGoogle Scholar
Landau, L.D. & Lifshitz, E.M. 1987 Chapter X - One-dimensional gas flow. In Fluid Mechanics, 2nd edn (ed. L.D. Landau & E.M. Lifshitz), pp. 361–413. Pergamon.CrossRefGoogle Scholar
Leshev, I. & Peev, G. 2003 Film flow on a horizontal rotating disk. Chem. Engng Process. 42 (11), 925–929.CrossRefGoogle Scholar
Li, Y., Sisoev, G.M. & Shikhmurzaev, Y.D. 2019 On the breakup of spiralling liquid jets. J. Fluid Mech. 862, 364–384.CrossRefGoogle Scholar
Mogilevskii, E.I. & Shkadov, V.Ya. 2009 Thin viscous fluid film flows over rotating curvilinear surfaces. Fluid Dyn. 44 (2), 189–201.CrossRefGoogle Scholar
Mohajer, B. & Li, R. 2015 Circular hydraulic jump on finite surfaces with capillary limit. Phys. Fluids 27 (11), 117102.CrossRefGoogle Scholar
Myers, T.G. & Lombe, M. 2006 The importance of the coriolis force on axisymmetric horizontal rotating thin film flows. Chem. Engng Process. 45 (2), 90–98.CrossRefGoogle Scholar
Needham, D.J. & Merkin, J.H. 1987 The development of nonlinear waves on the surface of a horizontally rotating thin liquid film. J. Fluid Mech. 184, 357–379.CrossRefGoogle Scholar
Ozar, B., Cetegen, B.M. & Faghri, A. 2003 Experiments on the flow of a thin liquid film over a horizontal stationary and rotating disk surface. Exp. Fluids 34 (5), 556–565.CrossRefGoogle Scholar
Pask, S.D., Nuyken, O. & Cai, Z. 2012 The spinning disk reactor: an example of a process intensification technology for polymers and particles. Polym. Chem. 3, 2698–2707.CrossRefGoogle Scholar
Phillips, K., Kuhlman, J., Mohebbi, M., Calandrelli, E. & Gray, D. 2008 Investigation of circular hydraulic jump behavior in microgravity. In 38th Fluid Dynamics Conference and Exhibit, AIAA 2008-4049, p. 4049. AIAA.CrossRefGoogle Scholar
Rayleigh, Lord 1914 On the theory of long waves and bores. Proc. R. Soc. Lond. A 90 (619), 324–328.Google Scholar
Rojas, N., Argentina, M. & Tirapegui, E. 2013 A progressive correction to the circular hydraulic jump scaling. Phys. Fluids 25 (4), 042105.CrossRefGoogle Scholar
Rozhdestvenskii, B.L. 1979 Application of exact solutions of the ‘shallow water’ equations to the explanation of the simplest flows. J. Appl. Mech. Tech. Phys. 20 (2), 140–143.CrossRefGoogle Scholar
Saberi, A., Mahpeykar, M.R. & Teymourtash, A.R. 2019 Experimental measurement of radius of circular hydraulic jumps: effect of radius of convex target plate. Flow Meas. Instrum. 65, 274–279.CrossRefGoogle Scholar
Scheichl, B. & Kluwick, A. 2019 Laminar spread of a circular liquid jet impinging axially on a rotating disc. J. Fluid Mech. 864, 449–489.10.1017/jfm.2018.1009CrossRefGoogle Scholar
Schlichting, H. & Gersten, K. 2016 Boundary-Layer Theory. Springer.Google Scholar
Shkadov, V.Ya. 1967 Wave flow regimes of a thin layer of viscous fluid subject to gravity. Fluid Dyn. 2 (1), 29–34.CrossRefGoogle Scholar
Shkadov, V.Ya. 1973 Some methods and problems of the theory of hydrodynamic stability. In Proceedings of Institute of Mechanics of Lomonosov Moscow State University.Google Scholar
Sisoev, G.M., Goldgof, D.B. & Korzhova, V.N. 2010 Stationary spiral waves in film flow over a spinning disk. Phys. Fluids 22 (5), 052106.CrossRefGoogle Scholar
Sisoev, G.M., Matar, O.K. & Lawrence, C.J. 2003 Axisymmetric wave regimes in viscous liquid film flow over a spinning disk. J. Fluid Mech. 495, 385–411.CrossRefGoogle Scholar
Sisoev, G.M., Tal'drik, A.F. & Shkadov, V.Ya. 1986 Flow of a viscous liquid film on the surface of a rotating disk. J. Engng Phys. 51 (4), 1171–1174.CrossRefGoogle Scholar
Tani, I. 1949 Water jump in the boundary layer. J. Phys. Soc. Japan 4 (4–6), 212–215.CrossRefGoogle Scholar
Thomas, S., Faghri, A. & Hankey, W. 1991 Experimental analysis and flow visualization of a thin liquid film on a stationary and rotating disk. Trans. ASME J. Fluids Engng 113 (1), 73–80.CrossRefGoogle Scholar
Trifonov, Yu. 2014 Stability of a film flowing down an inclined corrugated plate: the direct Navier–Stokes computations and Floquet theory. Phys. Fluids 26 (11), 114101-1–114101-15.CrossRefGoogle Scholar
Volovik, G.E. 2005 Hydraulic jump as a white hole. J. Expl Theor. Phys. Lett. 82 (10), 624–627.CrossRefGoogle Scholar
Wang, D., Jin, H., Ling, X., Peng, H., Yu, J. & Cui, Z. 2020 Regulation of velocity zoning behaviour and hydraulic jump of impinging jet flow on a spinning disk reactor. Chem. Engng J. 390, 124392.CrossRefGoogle Scholar
Wang, Y. & Khayat, R.E. 2018 Impinging jet flow and hydraulic jump on a rotating disk. J. Fluid Mech. 839, 525–560.CrossRefGoogle Scholar
Wang, Y. & Khayat, R.E. 2019 The role of gravity in the prediction of the circular hydraulic jump radius for high-viscosity liquids. J. Fluid Mech. 862, 128–161.CrossRefGoogle Scholar
Watanabe, S., Putkaradze, V. & Bohr, T. 2003 Integral methods for shallow free-surface flows with separation. J. Fluid Mech. 480, 233–265.CrossRefGoogle Scholar
Watson, E.J. 1964 The radial spread of a liquid jet over a horizontal plane. J. Fluid Mech. 20 (3), 481–499.CrossRefGoogle Scholar
Weinstein, S.J. & Ruschak, K.J. 2004 Coating flows. Annu. Rev. Fluid Mech. 36 (1), 29–53.CrossRefGoogle Scholar