Article contents
Statistical structure of self-sustaining attached eddies in turbulent channel flow
Published online by Cambridge University Press: 12 February 2015
Abstract
The linear growth of the spanwise correlation length scale with the distance from the wall in the logarithmic region of wall-bounded turbulent flows has been understood as a reflection of Townsend’s attached eddies. Based on this observation, in the present study, we perform a numerical experiment, which simulates energy-containing motions only at a given spanwise length scale in the logarithmic region, using their self-sustaining nature found recently. The self-sustaining energy-containing motions at each of the spanwise length scales are found to be self-similar with respect to the given spanwise length. Furthermore, their statistical structures are consistent with those of the attached eddies in the original theory, providing direct evidence on the existence of Townsend’s attached eddies. It is shown that a single self-sustaining attached eddy is composed of two distinct elements, one of which is a long streaky motion reaching the near-wall region, and the other is a relatively short vortical structure carrying all the velocity components. For the given spanwise length  ${\it\lambda}_{z}$ between
${\it\lambda}_{z}$ between 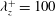 ${\it\lambda}_{z}^{+}=100$ and
${\it\lambda}_{z}^{+}=100$ and  ${\it\lambda}_{z}\simeq 1.5h$, where
${\it\lambda}_{z}\simeq 1.5h$, where  $h$ is half the height of the channel, the former is found to be self-similar along
$h$ is half the height of the channel, the former is found to be self-similar along  $y\simeq 0.1{\it\lambda}_{z}$ and
$y\simeq 0.1{\it\lambda}_{z}$ and  ${\it\lambda}_{x}\simeq 10{\it\lambda}_{z}$, while the latter is self-similar along
${\it\lambda}_{x}\simeq 10{\it\lambda}_{z}$, while the latter is self-similar along  $y\simeq 0.5{\it\lambda}_{z}\sim 0.7{\it\lambda}_{z}$ and
$y\simeq 0.5{\it\lambda}_{z}\sim 0.7{\it\lambda}_{z}$ and  ${\it\lambda}_{x}\simeq 2{\it\lambda}_{z}\sim 3{\it\lambda}_{z}$ where
${\it\lambda}_{x}\simeq 2{\it\lambda}_{z}\sim 3{\it\lambda}_{z}$ where  $y$ is the wall-normal direction. The scaling suggests that the smallest attached eddy would be a near-wall coherent motion in the form of a streak and quasi-streamwise vortices aligned to that, whereas the largest one would be an outer motion with a very-large-scale motion (VLSM) and large-scale motions (LSMs) aligned to that. The attached eddies in between, the size of which is proportional to their distance from the wall, contribute to the logarithmic region and fill the space caused by the length scale separation. The scaling is also found to yield behaviour consistent with the emergence of
$y$ is the wall-normal direction. The scaling suggests that the smallest attached eddy would be a near-wall coherent motion in the form of a streak and quasi-streamwise vortices aligned to that, whereas the largest one would be an outer motion with a very-large-scale motion (VLSM) and large-scale motions (LSMs) aligned to that. The attached eddies in between, the size of which is proportional to their distance from the wall, contribute to the logarithmic region and fill the space caused by the length scale separation. The scaling is also found to yield behaviour consistent with the emergence of  $k_{x}^{-1}$ spectra in a number of previous studies. Finally, a further discussion is provided, in particular on Townsend’s inactive motion and several recent theoretical findings.
$k_{x}^{-1}$ spectra in a number of previous studies. Finally, a further discussion is provided, in particular on Townsend’s inactive motion and several recent theoretical findings.
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 176
- Cited by



