Article contents
Stable equilibrium configurations of an oblate capsule in simple shear flow
Published online by Cambridge University Press: 24 February 2016
Abstract
The objective of the paper is to determine the stable mechanical equilibrium states of an oblate capsule subjected to a simple shear flow, by positioning its revolution axis initially off the shear plane. We consider an oblate capsule with a strain-hardening membrane and investigate the influence of the initial orientation, capsule aspect ratio 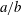 $a/b$, viscosity ratio
$a/b$, viscosity ratio 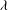 ${\it\lambda}$ between the internal and external fluids and the capillary number
${\it\lambda}$ between the internal and external fluids and the capillary number 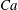 $Ca$ which compares the viscous to the elastic forces. A numerical model coupling the finite element and boundary integral methods is used to solve the three-dimensional fluid–structure interaction problem. For any initial orientation, the capsule converges towards the same mechanical equilibrium state, which is only a function of the capillary number and viscosity ratio. For
$Ca$ which compares the viscous to the elastic forces. A numerical model coupling the finite element and boundary integral methods is used to solve the three-dimensional fluid–structure interaction problem. For any initial orientation, the capsule converges towards the same mechanical equilibrium state, which is only a function of the capillary number and viscosity ratio. For 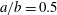 $a/b=0.5$, only four regimes are stable when
$a/b=0.5$, only four regimes are stable when 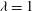 ${\it\lambda}=1$: tumbling and swinging in the low and medium
${\it\lambda}=1$: tumbling and swinging in the low and medium 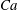 $Ca$ range (
$Ca$ range (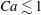 $Ca\lesssim 1$), regimes for which the capsule revolution axis is contained within the shear plane; then wobbling during which the capsule experiences precession around the vorticity axis; and finally rolling along the vorticity axis at high capillary numbers. When
$Ca\lesssim 1$), regimes for which the capsule revolution axis is contained within the shear plane; then wobbling during which the capsule experiences precession around the vorticity axis; and finally rolling along the vorticity axis at high capillary numbers. When 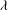 ${\it\lambda}$ is increased, the tumbling-to-swinging transition occurs for higher
${\it\lambda}$ is increased, the tumbling-to-swinging transition occurs for higher 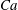 $Ca$; the wobbling regime takes place at lower
$Ca$; the wobbling regime takes place at lower  $Ca$ values and within a narrower
$Ca$ values and within a narrower  $Ca$ range. For
$Ca$ range. For 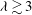 ${\it\lambda}\gtrsim 3$, the swinging regime completely disappears, which indicates that the stable equilibrium states are mainly the tumbling and rolling regimes at higher viscosity ratios. We finally show that the
${\it\lambda}\gtrsim 3$, the swinging regime completely disappears, which indicates that the stable equilibrium states are mainly the tumbling and rolling regimes at higher viscosity ratios. We finally show that the 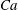 $Ca$–
$Ca$–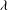 ${\it\lambda}$ phase diagram is qualitatively similar for higher aspect ratio. Only the
${\it\lambda}$ phase diagram is qualitatively similar for higher aspect ratio. Only the 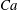 $Ca$-range over which wobbling is stable increases with
$Ca$-range over which wobbling is stable increases with 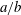 $a/b$, restricting the stability ranges of in- and out-of-plane motions, although this phenomenon is mainly visible for viscosity ratios larger than 1.
$a/b$, restricting the stability ranges of in- and out-of-plane motions, although this phenomenon is mainly visible for viscosity ratios larger than 1.
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
Dupont et al. supplementary movie
Tumbling motion of an oblate capsule (aspect ratio of 0.5, strain-hardening Skalak membrane). The initial inclination ζ0 of the revolution axis with the vorticity axis of the shear flow is 45°; the capillary number is Ca = 0.01 and the internal to external viscosity ratio λ = 1. The point M3(t) is the location at time t of the membrane point located at the tip of the short axis. The point A3 (t) is the location at time t of the membrane point that used to be located on the short axis initially. The shear plane of the external flow, represented in blue, passes through the capsule centre of mass.
Dupont et al. supplementary movie
Swinging motion of an oblate capsule (aspect ratio of 0.5, strain-hardening Skalak membrane). The initial inclination ζ0 of the revolution axis with the vorticity axis of the shear flow is 30°; the capillary number is Ca = 0.03 and the internal to external viscosity ratio λ = 1. The point M3(t) is the location at time t of the membrane point located at the tip of the short axis. The point A3(t) is the location at time t of the membrane point that used to be located on the short axis initially. The shear plane of the external flow, represented in blue, passes through the capsule centre of mass.
Dupont et al. supplementary movie
Motion of transition between the swinging and rolling regimes with precession around the vorticity axis for an oblate capsule (aspect ratio of 0.5, strain-hardening Skalak membrane). The initial inclination ζ0 of the revolution axis with the vorticity axis of the shear flow is 45°; the capillary number is Ca = 0.9 and the internal to external viscosity ratio λ = 1. The point M3(t) is the location at time t of the membrane point located at the tip of the short axis. The point A3(t) is the location at time t of the membrane point that used to be located on the short axis initially. The shear plane of the external flow, represented in blue, passes through the capsule centre of mass.
Dupont et al. supplementary movie
Rolling motion of an oblate capsule (aspect ratio of 0.5, strain-hardening Skalak membrane). The initial inclination ζ0 of the revolution axis with the vorticity axis of the shear flow is 15°; the capillary number is Ca = 2 and the internal to external viscosity ratio λ = 1.The point M3(t) is the location at time t of the membrane point located at the tip of the short axis. The point A3(t) is the location at time t of the membrane point that used to be located on the short axis initially. The shear plane of the external flow, represented in blue, passes through the capsule centre of mass.
Dupont et al. supplementary movie
Relaxation to rest of an oblate capsule (aspect ratio of 0.5, strain-hardening Skalak membrane) experiencing a steady rolling regime. The initial inclination ζ0 of the revolution axis with the vorticity axis of the shear flow is 15°; the capillary number is Ca = 2 and the internal to external viscosity ratio λ = 1. The point M3(t) is the location at time t of the membrane point located at the tip of the short axis. The point A3(t) is the location at time t of the membrane point that used to be located on the short axis initially. The shear plane of the external flow, represented in blue, passes through the capsule centre of mass. The movie encoding speed was decreased by a factor 20 compared to the other films to enable the visualization of the relaxation phenomenon.
- 20
- Cited by



