Published online by Cambridge University Press: 23 June 2017
We investigate the spatial stability of compressible, viscous pipe flows with radius-dependent mean density profiles, subjected to solid body rotations. For a fixed Rossby number  $\unicode[STIX]{x1D716}$ (inverse of the rotational speed), as the Reynolds number
$\unicode[STIX]{x1D716}$ (inverse of the rotational speed), as the Reynolds number 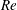 $Re$ is increased, the flow transitions from being stable to convectively unstable, usually leading to absolute instability. If flow compressibility is unimportant and
$Re$ is increased, the flow transitions from being stable to convectively unstable, usually leading to absolute instability. If flow compressibility is unimportant and 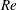 $Re$ is held constant, there appears to be a maximum
$Re$ is held constant, there appears to be a maximum 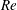 $Re$ below which the flow remains stable irrespective of any rotational speed, or a minimum azimuthal Reynolds number
$Re$ below which the flow remains stable irrespective of any rotational speed, or a minimum azimuthal Reynolds number 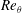 $Re_{\unicode[STIX]{x1D703}}$
$Re_{\unicode[STIX]{x1D703}}$ 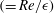 $(=Re/\unicode[STIX]{x1D716})$ is required for any occurrence of absolute instabilities. Once compressible forces are significant, the effect of pressure–density coupling is found to be more severe below a critical
$(=Re/\unicode[STIX]{x1D716})$ is required for any occurrence of absolute instabilities. Once compressible forces are significant, the effect of pressure–density coupling is found to be more severe below a critical 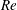 $Re$, where as rotational speeds are raised, a stable flow almost directly transitions to an absolutely unstable state. This happens at a critical
$Re$, where as rotational speeds are raised, a stable flow almost directly transitions to an absolutely unstable state. This happens at a critical 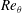 $Re_{\unicode[STIX]{x1D703}}$ which reduces with increased flow Mach number, pointing to compressibility aiding in the instability at these lower Reynolds numbers. However, at higher
$Re_{\unicode[STIX]{x1D703}}$ which reduces with increased flow Mach number, pointing to compressibility aiding in the instability at these lower Reynolds numbers. However, at higher 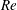 $Re$, above the critical value, the traditional stabilizing role of compressibility is recovered if mean density stratification exists, where the gradients of density play an equally important role, more so at the higher azimuthal modes. A total disturbance energy-based formulation is used to obtain mechanistic understanding at these stability states, where we find the entropic energy perturbations to dominate as the primary instability mechanism, in sharp contrast to the energy due to axial shear, known to play a leading role in incompressible swirling flows.
$Re$, above the critical value, the traditional stabilizing role of compressibility is recovered if mean density stratification exists, where the gradients of density play an equally important role, more so at the higher azimuthal modes. A total disturbance energy-based formulation is used to obtain mechanistic understanding at these stability states, where we find the entropic energy perturbations to dominate as the primary instability mechanism, in sharp contrast to the energy due to axial shear, known to play a leading role in incompressible swirling flows.