Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-28T23:28:41.707Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability of a moving radial liquid sheet: experiments

Published online by Cambridge University Press:  08 April 2015

Manjula Paramati ,
Mahesh S. Tirumkudulu Open the ORCID record for Mahesh S. Tirumkudulu [Opens in a new window]  and
Peter J. Schmid
Manjula Paramati
Affiliation:
Department of Chemical Engineering, Indian Institute of Technology Bombay, Powai, Mumbai 400076, India
Mahesh S. Tirumkudulu*
Affiliation:
Department of Chemical Engineering, Indian Institute of Technology Bombay, Powai, Mumbai 400076, India
Peter J. Schmid
Affiliation:
Department of Mathematics, Imperial College London, London SW7 2AZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A recent theory (Tirumkudulu & Paramati, Phys. Fluids, vol. 25, 2013, 102107) for a radially expanding liquid sheet, that accounts for liquid inertia, interfacial tension and thinning of the liquid sheet while ignoring the inertia of the surrounding gas and viscous effects, shows that such a sheet is convectively unstable to small sinuous disturbances at all frequencies and Weber numbers 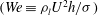$(We\equiv {\it\rho}_{l}U^{2}h/{\it\sigma})$. Here, 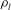${\it\rho}_{l}$ and ${\it\sigma}$ are the density and surface tension of the liquid, respectively, 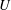$U$ is the speed of the liquid jet, and 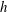$h$ is the local sheet thickness. In this study we use a simple non-contact optical technique based on laser-induced fluorescence (LIF) to measure the instantaneous local sheet thickness and displacement of a circular sheet produced by head-on impingement of two laminar jets. When the impingement point is disturbed via acoustic forcing, sinuous waves produced close to the impingement point travel radially outwards. The phase speed of the sinuous wave decreases while the amplitude grows as they propagate radially outwards. Our experimental technique was unable to detect thickness modulations in the presence of forcing, suggesting that the modulations could be smaller than the resolution of our experimental technique. The measured phase speed of the sinuous wave envelope matches with theoretical predictions while there is a qualitative agreement in the case of spatial growth. We show that there is a range of frequencies over which the sheet is unstable due to both aerodynamic interaction and thinning effects, while outside this range, thinning effects dominate. These results imply that a full theory that describes the dynamics of a radially expanding liquid sheet should account for both effects.

JFM classification

Instability: Absolute/convective instability Interfacial Flows (free surface): Interfacial Flows (free surface) Interfacial Flows (free surface): Thin films
Type
Papers
Information
Journal of Fluid Mechanics , Volume 770 , 10 May 2015 , pp. 398 - 423
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alekseenko, S., Antipin, V., Cherdantsev, A., Kharlamov, S. & Markovich, D. 2009 Two-wave structure of liquid film and wave interrelation in annular gas liquid flow with and without entrainment. Phys. Fluids 21, 1–5.CrossRefGoogle Scholar
Ashgriz, N.(Ed.) 2011 Handbook of Atomization and Sprays, 1st edn. Springer.CrossRefGoogle Scholar
Birge, R. R. 1987 KODAK Laser Dyes. Eastman Kodak Company.Google Scholar
Boudaoud, A., Couder, Y. & Amar, M. B. 1999 Self-adaptation in vibrating soap films. Phys. Rev. Lett. 82, 3847–3850.CrossRefGoogle Scholar
Bremond, N., Clanet, C. & Villermaux, E. 2007 Atomization of undulating liquid sheet. Phys. Fluids 585, 421–456.Google Scholar
Brown, R. C., Andruessi, P. & Zanelli, S. 1978 The use of wire probes for the measurement of liquid film thickness in annular gas–liquid flows. J. Chem. Engng 56, 754–757.Google Scholar
Choo, Y. J. & Kang, B. S. 2001 Parametric study on impinging jet liquid sheet thickness distribution using an interferometric method. Exp. Fluids 31, 56–62.CrossRefGoogle Scholar
Clark, G. D., Dombrowski, N. & Pyott, G. A. D. 1975 Large amplitude Kelvin–Helmholtz waves on thin liquid sheets. Proc. R. Soc. Lond. A 342 (1629), 209–224.Google Scholar
Crapper, G. D. & Dombrowski, N. 1984 A note on the effect of forced disturbances on the stability of thin liquid sheets and on the resulting drop size. Intl J. Multiphase Flow 10 (6), 731–736.CrossRefGoogle Scholar
Crimaldi, J. P. 2008 Planar laser induced fluorescence in aqueous flows. Exp. Fluids 44, 851–863.CrossRefGoogle Scholar
Dombrowski, N., Hasson, D. & Ward, D. E. 1960 Some aspects of liquid flow through fan spray nozzles. Chem. Engng Sci. 12, 35–50.CrossRefGoogle Scholar
Hidrovo, H. C. & Douglas, H. 2001 Emission and reabsorption of a laser induced fluorescence film thickness measurement. Meas. Sci. Technol. 12, 467–477.CrossRefGoogle Scholar
Huang, J. C. P. 1970 The break-up of axisymmetric liquid sheets. J. Fluid Mech. 43, 305–319.CrossRefGoogle Scholar
Liang, N. Y. & Chan, C. K. 1997 Fast thickness profile measurement of a thin film by using a line scan charge coupled device camera. Rev. Sci. Instrum. 68, 4525–4530.CrossRefGoogle Scholar
Lin, S. P. & Jiang, W. Y. 2003 Absolute and convective instability of a radially expanding liquid sheet. Phys. Fluids 15, 1745–1754.CrossRefGoogle Scholar
Matsumoto, S. & Takashima, Y. 1971 Studies of the standard deviation of sprayed drop size distribution. J. Chem. Engng Japan 4 (3), 53–59.CrossRefGoogle Scholar
Mulmule, A., Tirumkudulu, M. S. & Ramamurthi, K. 2010 Instability of a moving liquid sheet in the presence of acoustic forcing. Phys. Fluids 22, 1–14.CrossRefGoogle Scholar
Shen, Y., Mitts, C. & Poulikakos, D. 1997 Holographic investigation of the effect of elevated ambient temperature on the atomization characteristics of impinging jet sprays. Atomiz. Sprays 7, 123–142.CrossRefGoogle Scholar
Squire, H. B. 1953 Investigation of the instability of a moving liquid film. Br. J. Appl. Phys. 4, 167–169.CrossRefGoogle Scholar
Tammisola, O., Sasaki, A., Lundell, F., Ma, M. & Soderberg, L. D. 2011 Stabilizing effect of surrounding gas flow on a plane liquid sheet. J. Fluid Mech. 672, 5–32.CrossRefGoogle Scholar
Taylor, G. I. 1959 The dynamics of thin sheets of fluid. Part II. Waves on fluid sheets. Proc. R. Soc. Lond. A 253, 296–312.Google Scholar
Tirumkudulu, M. S. & Paramati, M. 2013 Stability of a moving radial liquid sheet: time-dependent equations. Phys. Fluids 25, 102107.CrossRefGoogle Scholar
Villermaux, E. & Clanet, C. 2002 Life of flapping liquid sheet. J. Fluid Mech. 462, 341–366.CrossRefGoogle Scholar
Wakimoto, T. & Azuma, T. 2004 Instability of radial liquid sheet flow. Trans. JSME 47, 9–19.Google Scholar
Weihs, D. 1978 Stability of thin, radially moving liquid sheets. J. Fluid Mech. 87, 289–298.CrossRefGoogle Scholar