Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-24T11:53:34.332Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability characteristics of a counter-rotating unequal-strength Batchelor vortex pair

Published online by Cambridge University Press:  06 March 2012

Kris Ryan ,
Christopher J. Butler  and
Gregory J. Sheard
Kris Ryan*
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, VIC 3800, Australia
Christopher J. Butler
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, VIC 3800, Australia
Gregory J. Sheard
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, VIC 3800, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A Batchelor vortex represents the asymptotic solution of a trailing vortex in an aircraft wake. In this study, an unequal-strength, counter-rotating Batchelor vortex pair is employed as a model of the wake emanating from one side of an aircraft wing; this model is a direct extension of several prior investigations that have considered unequal-strength Lamb–Oseen vortices as representations of the aircraft wake problem. Both solution of the linearized Navier–Stokes equations and direct numerical simulations are employed to study the linear and nonlinear development of a vortex pair with a circulation ratio of 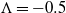. In contrast to prior investigations considering a Lamb–Oseen vortex pair, we note strong growth of the Kelvin mode 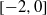coupled with an almost equal growth rate of the Crow instability. Three stages of nonlinear instability development are defined. In the initial stage, the Kelvin mode amplitude becomes sufficiently large that oscillations within the core of the weaker vortex are easily observable and significantly affect the profile of the weaker vortex. In the secondary stage, filaments of secondary vorticity emanate from the weaker vortex and are convected around the stronger vortex. In the tertiary stage, a transition in the dominant instability wavelength is observed from the short-wavelength Kelvin mode to the longer-wavelength Crow instability. Much of the instability growth is observed on the weaker vortex of the pair, although small perturbations in the stronger vortex are observed in the tertiary nonlinear growth phase.

JFM classification

Vortex Flows: Vortex dynamics Vortex Flows: Vortex instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 696 , 10 April 2012 , pp. 374 - 401
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Ash, R. L. & Khorrami, M. R. 1995 Vortex stability. In Fluid Vortices (ed. Green, S. I. ), chap. 8, pp. 317–372. Kluwer.Google Scholar
2. Batchelor, G. K. 1964 Axial flow in trailing line vortices. J. Fluid Mech. 20 (4), 645–658.Google Scholar
3. Blackburn, H. M. & Sheard, G. J. 2010 On quasi-periodic and subharmonic Floquet wake instabilities. Phys. Fluids 22 (3), 031701.CrossRefGoogle Scholar
4. Blackburn, H. M. & Sherwin, S. J. 2004 Formulation of a Galerkin spectral element–Fourier method for three-dimensional incompressible flows in cylindrical geometries. J. Comput. Phys. 197 (2), 759–778.CrossRefGoogle Scholar
5. Bristol, R. L., Ortega, J. M., Marcus, P. S. & Savaş, Ö. 2004 On cooperative instabilities of parallel vortex pairs. J. Fluid Mech. 517, 331–358.Google Scholar
6. Crouch, J. D. 1997 Instability and transient growth for two trailing-vortex pairs. J. Fluid Mech. 350, 311–330.Google Scholar
7. Crow, S. C. 1970 Stability theory for a pair of trailing vortices. AIAA J. 8 (12), 2172–2179.Google Scholar
8. Eloy, C. & Le Dizès, S. 1999 Three-dimensional instability of Burgers and Lamb–Oseen vortices in a strain field. J. Fluid Mech. 378, 145–166.CrossRefGoogle Scholar
9. Fabre, D., Jacquin, L. & Loof, A. 2002 Optimal perturbations in a four-vortex aircraft wake in counter-rotating configuration. J. Fluid Mech. 451, 319–328.CrossRefGoogle Scholar
10. Garten, J. F., Werne, J., Fritts, D. C. & Arendt, S. 2001 Direct numerical simulations of the Crow instability and subsequent vortex reconnection in a stratified flow. J. Fluid Mech. 426, 1–45.Google Scholar
11. Heaton, C. J. 2007 Centre modes in inviscid swirling flows, and their application to the stability of the Batchelor vortex. J. Fluid Mech. 576, 325–348.CrossRefGoogle Scholar
12. Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
13. Jimenez, J. 1975 Stability of a pair of corotating vortices. Phys. Fluids 18, 1580–1581.Google Scholar
14. Karniadakis, G. E., Israeli, M. & Orszag, S. A. 1991 High-order splitting methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 97 (2), 414–443.CrossRefGoogle Scholar
15. Karniadakis, G. E. & Sherwin, S. J. 2005 Spectral/hp Element Methods for Computational Fluid Dynamics, 2nd edn. Oxford University Press.CrossRefGoogle Scholar
16. Karniadakis, G. E. & Triantafyllou, G. S. 1992 Three-dimensional dynamics and transition to turbulence in the wake of bluff objects. J. Fluid Mech. 238, 1–30.Google Scholar
17. Kerswell, R. R. 2002 Elliptical instability. Annu. Rev. Fluid Mech. 34, 83–113.CrossRefGoogle Scholar
18. Lacaze, L., Birbaud, A.-L. & Le Dizès, S. 2005 Elliptic instability in a Rankine vortex with axial flow. Phys. Fluids 17, 017101–1.Google Scholar
19. Lacaze, L., Ryan, K. & Le Dizès, S. 2007 Elliptic instability in a strained Batchelor vortex. J. Fluid Mech. 577, 341–361.CrossRefGoogle Scholar
20. Laporte, F. & Corjon, A. 2000 Direct numerical simulations of the elliptic instability of a vortex pair. Phys. Fluids 12, 1016–1031.CrossRefGoogle Scholar
21. Le Dizès, S. & Laporte, F. 2002 Theoretical predictions for the elliptical instability in a two-vortex flow. J. Fluid Mech. 471, 169–201.CrossRefGoogle Scholar
22. Le Dizès, S. & Verga, A. 2002 Viscous interactions of two co-rotating vortices before merging. J. Fluid Mech. 467, 389–410.Google Scholar
23. Leweke, T. & Williamson, C. H. K. 1998 Cooperative elliptic instability of a vortex pair. J. Fluid Mech. 360, 85–119.Google Scholar
24. Leweke, T. & Williamson, C. H. K. 2011 Experiments on long-wavelength instability and reconnection of a vortex pair. Phys. Fluids 23, 024101.Google Scholar
25. Kelvin, Lord 1880 Vibrations of a columnar vortex. Phil. Mag. 10, 155–168.Google Scholar
26. Mariotti, A., Legras, B. & Dritschel, D. G. 1994 Vortex stripping and the erosion of coherent structures in two-dimensional flows. Phys. Fluids 6, 3954.Google Scholar
27. Marshall, J. S., Brancher, P. & Giovannini, A. 2001 Interaction of unequal anti-parallel vortex tubes. J. Fluid Mech. 446, 229–252.CrossRefGoogle Scholar
28. Meunier, P. & Leweke, T. 2005 Elliptic instability of a co-rotating vortex pair. J. Fluid Mech. 533, 125–159.Google Scholar
29. Moore, D. W. & Saffman, P. G. 1975 The instability of a straight vortex filament in a strain field. Proc. R. Soc. Lond. A 346, 413–425.Google Scholar
30. Ortega, J. M., Bristol, R. L. & Savaş, Ö. 2003 Experimental study of the instability of unequal-strength counter-rotating vortex pairs. J. Fluid Mech. 474, 35–84.CrossRefGoogle Scholar
31. Roy, C., Leweke, T., Thompson, M. C. & Hourigan, K. 2011 Experiments on the elliptic instability in vortex pairs with axial core flow. J. Fluid Mech. 677, 383–416.Google Scholar
32. Roy, C., Schaeffer, N., Le Dizès, S. & Thompson, M. C. 2008 Stability of a pair of co-rotating vortices with axial flow. Phys. Fluids 20, 094101.Google Scholar
33. Ryan, K. & Sheard, G. J. 2007 Nonlinear growth of short-wave instabilities in a Batchelor vortex pair. In Proceedings of the 16th Australasian Fluid Mechanics Conference, School of Engineering, The University of Queensland (ed. Jacobs, P., McIntyre, T., Cleary, M., Buttsworth, D., Mee, D., Clements, R., Morgan, R. & Lemckert, C. ). pp. 1463–1469.Google Scholar
34. Saffman, P. G. 1992 Vortex Dynamics. Cambridge University Press.Google Scholar
35. Schaeffer, N. & Le Dizès, S. 2010 Nonlinear dynamics of the elliptic instability. J. Fluid Mech. 646, 471–480.CrossRefGoogle Scholar
36. Scorer, R. S. & Davenport, L. J. 1970 Contrails and aircraft downwash. J. Fluid Mech. 43 (3), 451–464.CrossRefGoogle Scholar
37. Sheard, G. J., Fitzgerald, M. J. & Ryan, K. 2009 Cylinders with square cross section: wake instabilities with incidence angle variation. J. Fluid Mech. 630, 43–69.Google Scholar
38. Sipp, D., Jacquin, L. & Cossu, C. 2000 Self-adaptation and viscous selection in concentrated two-dimensional vortex dipoles. Phys. Fluids 12, 245.Google Scholar
39. So, J., Ryan, K. & Sheard, G. J. 2011 Short-wave instabilities on a vortex pair of unequal strength circulation ratio. Appl. Math. Model. 35 (4), 1581–1590.CrossRefGoogle Scholar
40. Thomas, P. J. & Auerbach, D. 1994 The observation of the simultaneous development of a long- and a short-wave instability mode on a vortex pair. J. Fluid Mech. 265, 289–302.Google Scholar
41. Thompson, M. C., Hourigan, K. & Sheridan, J. 1996 Three-dimensional instabilities in the wake of a circular cylinder. Exp. Therm. Fluid Sci. 12 (2), 190–196.Google Scholar
42. Tsai, C.-Y. & Widnall, S. E. 1976 The stability of short waves on a straight vortex filament in a weak externally imposed strain field. J. Fluid Mech. 76, 721–733.Google Scholar
43. Widnall, S. E., Bliss, D. B. & Tsai, C.-Y. 1974 The instability of short waves on a vortex ring. J. Fluid Mech. 66, 35–47.CrossRefGoogle Scholar