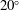1 Introduction
Volvox is a genus of algae with spherical, free-swimming colonies consisting of up to 50 000 surface somatic cells embedded in an extracellular matrix and a small number of interior germ cells which develop to become the next generation (figure 1). Discovered by van Leeuwenhoek (Reference van Leeuwenhoek1700), who marvelled at their graceful swimming, it was named by Linnaeus (Reference Linnaeus1758) for its characteristic spinning motion. The colony swims in a direction parallel to its anterior–posterior axis thanks to the beating of a pair of flagella on each somatic cell. All flagella exhibit an approximately coplanar, meridional beat, with the power stroke directed towards the rear, i.e. from the north pole towards the south pole, except that the plane of beating is in fact offset from a purely meridional plane by an angle of
![]() $10$
–
$10$
–
![]() $20^{\circ }$
. It is believed that this offset causes the observed rotation (Hoops Reference Hoops1993, Reference Hoops1997). The colonies are about 0.3 % denser than water, and swim upwards in still water; this is because the relatively dense interior cells are clustered towards the rear, so when the anterior–posterior axis is deflected from vertical, the colony experiences a restoring gravitational torque that competes with a viscous torque to right the colony on a timescale of
$20^{\circ }$
. It is believed that this offset causes the observed rotation (Hoops Reference Hoops1993, Reference Hoops1997). The colonies are about 0.3 % denser than water, and swim upwards in still water; this is because the relatively dense interior cells are clustered towards the rear, so when the anterior–posterior axis is deflected from vertical, the colony experiences a restoring gravitational torque that competes with a viscous torque to right the colony on a timescale of
![]() ${\sim}10~\text{s}$
. It is remarkable that a typical, free-swimming Volvox colony swims in a constant (vertical) direction, suggesting axially symmetric coordination of the flagellar beating, and that it clearly rotates about the axis of symmetry.
${\sim}10~\text{s}$
. It is remarkable that a typical, free-swimming Volvox colony swims in a constant (vertical) direction, suggesting axially symmetric coordination of the flagellar beating, and that it clearly rotates about the axis of symmetry.

Figure 1. A colony of Volvox carteri. Small green dots are the somatic cells on the outside (2000–6000 for V. carteri); larger green spheroids are the interior daughter colonies. The photograph is taken from above, as the colony swims upwards towards the camera.
1.1 Experimental background
During its 48-h life cycle, the size of a Volvox colony increases, though the number and size of somatic cells do not. Thus one would expect the sedimentation speed
![]() $V$
of a colony whose swimming was arrested to increase with colony radius
$V$
of a colony whose swimming was arrested to increase with colony radius
![]() $a_{0}$
, while its upswimming speed
$a_{0}$
, while its upswimming speed
![]() $U_{1}$
would decrease, both because of the increase in
$U_{1}$
would decrease, both because of the increase in
![]() $V$
and because, even if it were neutrally buoyant, one would expect the viscous drag to increase with size and hence the swimming speed
$V$
and because, even if it were neutrally buoyant, one would expect the viscous drag to increase with size and hence the swimming speed
![]() $U$
to decrease. Presumably the angular velocity about the axis,
$U$
to decrease. Presumably the angular velocity about the axis,
![]() ${\it\Omega}$
, would also decrease. Drescher et al. (Reference Drescher, Leptos, Tuval, Ishikawa, Pedley and Goldstein2009) measured the swimming speeds, sedimentation speeds, and angular velocities of 78, 81 and 61 colonies of V. carteri, respectively, ranging in radius from about
${\it\Omega}$
, would also decrease. Drescher et al. (Reference Drescher, Leptos, Tuval, Ishikawa, Pedley and Goldstein2009) measured the swimming speeds, sedimentation speeds, and angular velocities of 78, 81 and 61 colonies of V. carteri, respectively, ranging in radius from about
![]() $100~{\rm\mu}\text{m}$
to about
$100~{\rm\mu}\text{m}$
to about
![]() $500~{\rm\mu}\text{m}$
. The results are shown in figure 2, where indeed both
$500~{\rm\mu}\text{m}$
. The results are shown in figure 2, where indeed both
![]() $U_{1}$
and
$U_{1}$
and
![]() ${\it\Omega}$
are seen to decrease with
${\it\Omega}$
are seen to decrease with
![]() $a_{0}$
, while
$a_{0}$
, while
![]() $V$
increases. The expected swimming speed if the colony were neutrally buoyant would be
$V$
increases. The expected swimming speed if the colony were neutrally buoyant would be
![]() $U=U_{1}+V$
(Solari et al.
Reference Solari, Ganguly, Kessler, Michod and Goldstein2006), where linearity is expected because the Reynolds number of even the largest colony is less than 0.1, so the fluid dynamics will be governed by the Stokes equations.
$U=U_{1}+V$
(Solari et al.
Reference Solari, Ganguly, Kessler, Michod and Goldstein2006), where linearity is expected because the Reynolds number of even the largest colony is less than 0.1, so the fluid dynamics will be governed by the Stokes equations.
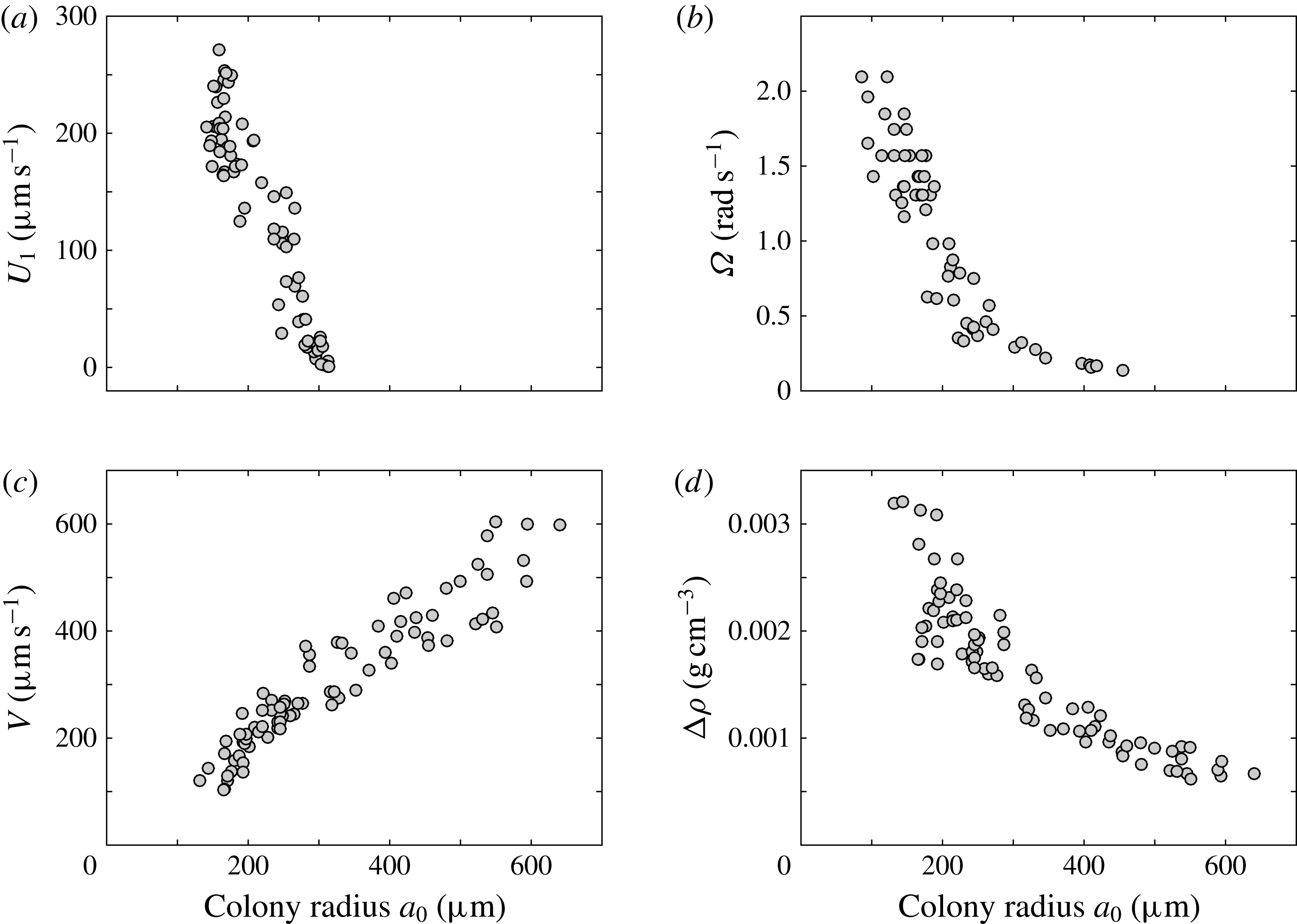
Figure 2. Swimming properties of V. carteri as a function of colony radius
![]() $a_{0}$
. Measured values of the (a) upswimming speed
$a_{0}$
. Measured values of the (a) upswimming speed
![]() $U_{1}$
, (b) angular velocity
$U_{1}$
, (b) angular velocity
![]() ${\it\Omega}$
and (c) sedimentation speed
${\it\Omega}$
and (c) sedimentation speed
![]() $V$
, as well as (d) the deduced density offset
$V$
, as well as (d) the deduced density offset
![]() ${\rm\Delta}{\it\rho}=9{\rm\mu}V/2ga_{0}^{2}$
compared with the surrounding medium. Adapted from Drescher et al. (Reference Drescher, Leptos, Tuval, Ishikawa, Pedley and Goldstein2009).
${\rm\Delta}{\it\rho}=9{\rm\mu}V/2ga_{0}^{2}$
compared with the surrounding medium. Adapted from Drescher et al. (Reference Drescher, Leptos, Tuval, Ishikawa, Pedley and Goldstein2009).
The purpose of this paper is to describe a model for Volvox swimming from which both
![]() $U$
and
$U$
and
![]() ${\it\Omega}$
can be predicted, and to compare the predictions with the experiments of figure 2. The input to the model will be the fluid velocities generated by the flagellar beating as measured by Brumley et al. (Reference Brumley, Polin, Pedley and Goldstein2012, Reference Brumley, Polin, Pedley and Goldstein2015a
,Reference Brumley, Rusconi, Son and Stocker
b
). Detailed measurements were made of the time-dependent flow fields produced by the beating flagella of numerous V. carteri colonies. Individual colonies were held in place on a micro-pipette in a
${\it\Omega}$
can be predicted, and to compare the predictions with the experiments of figure 2. The input to the model will be the fluid velocities generated by the flagellar beating as measured by Brumley et al. (Reference Brumley, Polin, Pedley and Goldstein2012, Reference Brumley, Polin, Pedley and Goldstein2015a
,Reference Brumley, Rusconi, Son and Stocker
b
). Detailed measurements were made of the time-dependent flow fields produced by the beating flagella of numerous V. carteri colonies. Individual colonies were held in place on a micro-pipette in a
![]() $25~\text{mm}\times 25~\text{mm}\times 5~\text{mm}$
glass observation chamber; the colonies were attached at the equator and arranged so that the symmetry axis of a colony was perpendicular both to the pipette and to the field of view of the observing microscope. The projection of the flow field onto the focal plane of the microscope was visualised by seeding the fluid medium with
$25~\text{mm}\times 25~\text{mm}\times 5~\text{mm}$
glass observation chamber; the colonies were attached at the equator and arranged so that the symmetry axis of a colony was perpendicular both to the pipette and to the field of view of the observing microscope. The projection of the flow field onto the focal plane of the microscope was visualised by seeding the fluid medium with
![]() $0.5~{\rm\mu}\text{m}$
polystyrene microspheres at a volume fraction of
$0.5~{\rm\mu}\text{m}$
polystyrene microspheres at a volume fraction of
![]() $2\times 10^{-4}$
, and 30-second-long high-speed movies were taken. The (projected) velocity field was measured using particle image velocimetry (PIV); a total of 60 different colonies were investigated, ranging in radius from
$2\times 10^{-4}$
, and 30-second-long high-speed movies were taken. The (projected) velocity field was measured using particle image velocimetry (PIV); a total of 60 different colonies were investigated, ranging in radius from
![]() $48~{\rm\mu}\text{m}$
to
$48~{\rm\mu}\text{m}$
to
![]() $251~{\rm\mu}\text{m}$
(mean
$251~{\rm\mu}\text{m}$
(mean
![]() $144\pm 43~{\rm\mu}\text{m}$
), the distribution of which is shown in figure 3.
$144\pm 43~{\rm\mu}\text{m}$
), the distribution of which is shown in figure 3.
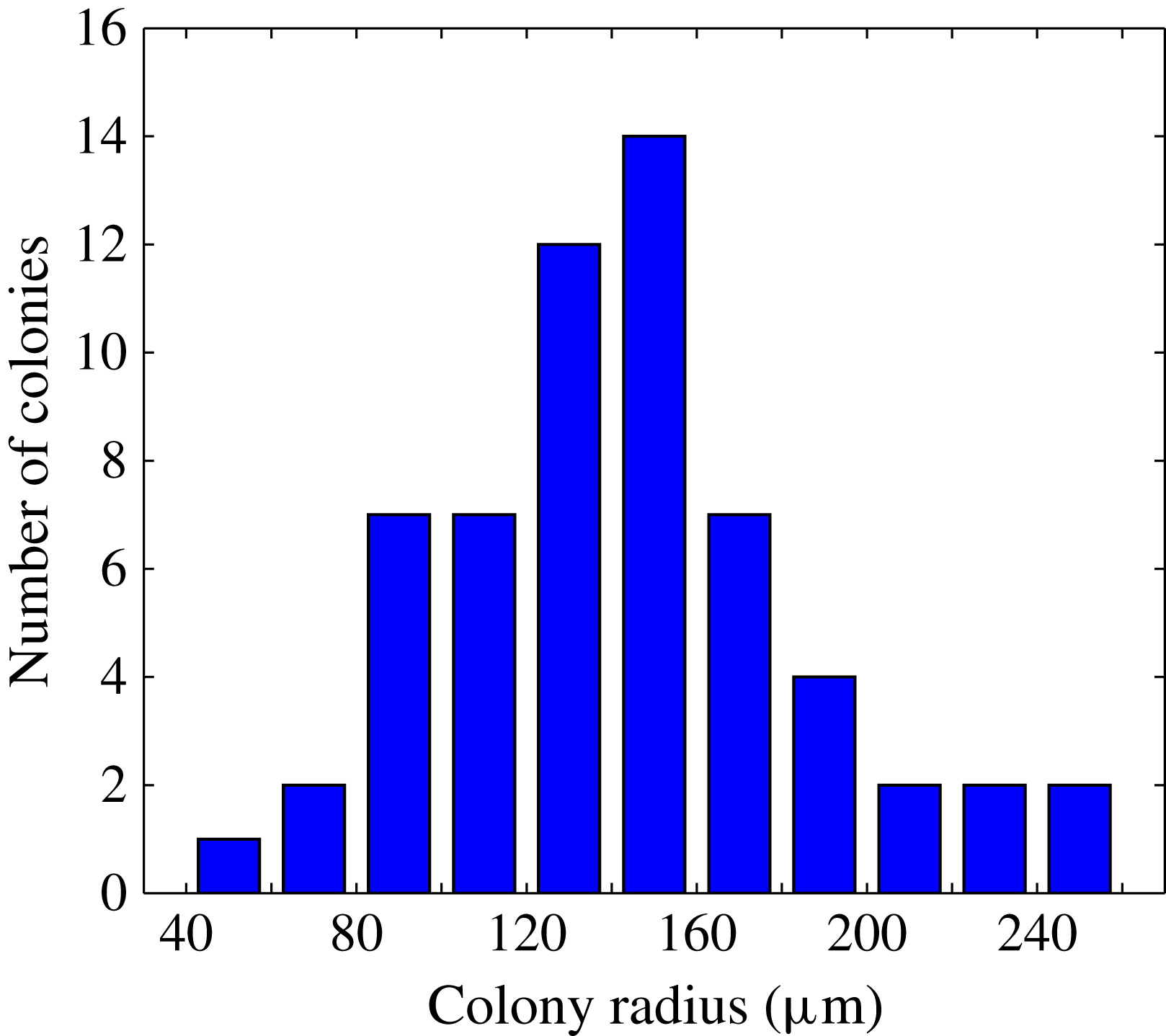
Figure 3. Distribution of colonies by radius, for which the metachronal wave properties are characterised. Adapted from figure 1(b) of Brumley et al. (Reference Brumley, Polin, Pedley and Goldstein2015a ).
One example of the time-averaged magnitude of the velocity distribution is shown in figure 4(a). This is a maximum near the equator because the flagellar beating drives a non-zero mean flow past the colony, parallel to the axis of symmetry and directed from front to back. This is consistent with the fact that untethered colonies swim forwards, parallel to the axis.

Figure 4. Experimental flow fields. (a) Magnitude (colour) and direction (arrows) of the time-averaged velocity field measured with PIV. Radial
![]() $u_{r}^{\prime }$
(b) and tangential
$u_{r}^{\prime }$
(b) and tangential
![]() $u_{{\it\theta}}^{\prime }$
(c) components of the unsteady fluid velocity field shown at various times through one flagellar beating cycle. Parts (a) and (b) are adapted from figures 1(c) and (d), respectively, of Brumley et al. (Reference Brumley, Polin, Pedley and Goldstein2015a
).
$u_{{\it\theta}}^{\prime }$
(c) components of the unsteady fluid velocity field shown at various times through one flagellar beating cycle. Parts (a) and (b) are adapted from figures 1(c) and (d), respectively, of Brumley et al. (Reference Brumley, Polin, Pedley and Goldstein2015a
).
Figure 5. Kymographs of radial
![]() $u_{r}^{\prime }$
(a) and tangential
$u_{r}^{\prime }$
(a) and tangential
![]() $u_{{\it\theta}}^{\prime }$
(b) velocity around Volvox colonies, measured at a radius of
$u_{{\it\theta}}^{\prime }$
(b) velocity around Volvox colonies, measured at a radius of
![]() $r=1.3\times a_{0}$
.
$r=1.3\times a_{0}$
.
More interesting are the perturbations to this mean flow. Time-dependent details of the velocity field can be seen in movies S1 and S2 which are available at http://dx.doi.org/10.1017/jfm.2016.306. Close to the colony surface, backwards and forwards motion, driven by the beating flagella, can be clearly seen; further away the flow is nearly steady. Figure 4 contains a series of snapshots showing unsteady components of (b) the radial velocity,
![]() $u_{r}^{\prime }$
, and (c) the tangential velocity,
$u_{r}^{\prime }$
, and (c) the tangential velocity,
![]() $u_{{\it\theta}}^{\prime }$
. It is immediately evident that the maximum of radial velocity propagates as a wave from front to back, in the same direction as the power stroke of the flagellar beat: a symplectic metachronal wave (Sleigh Reference Sleigh1962). This is further demonstrated in figure 5 which shows kymographs of
$u_{{\it\theta}}^{\prime }$
. It is immediately evident that the maximum of radial velocity propagates as a wave from front to back, in the same direction as the power stroke of the flagellar beat: a symplectic metachronal wave (Sleigh Reference Sleigh1962). This is further demonstrated in figure 5 which shows kymographs of
![]() $u_{r}$
and
$u_{r}$
and
![]() $u_{{\it\theta}}$
measured at a distance
$u_{{\it\theta}}$
measured at a distance
![]() $r=1.3\times a_{0}$
from the colony surface: the propagating wave is clearly seen in figure 5(a), which includes evidence of an interesting phase defect, while figure 5(b) suggests that the tangential velocity behaves more like a standing wave, dominated by the power stroke near the equator. (The mechanism underlying the coordination of the flagellar beats between the thousands of quite widely spaced somatic cells is itself thought to stem from the fluid mechanical interaction between them. Brumley et al. (Reference Brumley, Polin, Pedley and Goldstein2015a
) developed a model for this coordination, as well as for phase defects; it will not be expanded on here.)
$r=1.3\times a_{0}$
from the colony surface: the propagating wave is clearly seen in figure 5(a), which includes evidence of an interesting phase defect, while figure 5(b) suggests that the tangential velocity behaves more like a standing wave, dominated by the power stroke near the equator. (The mechanism underlying the coordination of the flagellar beats between the thousands of quite widely spaced somatic cells is itself thought to stem from the fluid mechanical interaction between them. Brumley et al. (Reference Brumley, Polin, Pedley and Goldstein2015a
) developed a model for this coordination, as well as for phase defects; it will not be expanded on here.)
Each set of velocity measurements by Brumley et al. (Reference Brumley, Polin, Pedley and Goldstein2012) are projections onto a single meridional plane. However, the clear axial symmetry of a Volvox colony, freely swimming and spinning, indicates that it is reasonable to assume that the flagellar displacement and the consequent velocity fields are also axisymmetric. The fact that the colonies were held fixed means that a force and torque were applied to them while the measurements were being made. This may mean that the flagellar displacements, relative to the colony surface, differed from those for the same colony when swimming freely. The same goes for any constraints felt by a pinned colony due to the proximity of the chamber walls, though this effect is probably small since the largest colonies have diameter around
![]() $500~{\rm\mu}\text{m}$
, about one tenth of the minimum chamber dimension. We have no direct evidence on these questions, and will assume that the two flagellar beats are the same.
$500~{\rm\mu}\text{m}$
, about one tenth of the minimum chamber dimension. We have no direct evidence on these questions, and will assume that the two flagellar beats are the same.
The results of Brumley et al. (Reference Brumley, Polin, Pedley and Goldstein2012) show that a good fit to the observations of the radial velocity perturbations is given by the following simple form:
where
![]() ${\it\theta}_{0}$
is the polar angle,
${\it\theta}_{0}$
is the polar angle,
![]() $k,{\it\sigma}$
are the wavenumber and frequency of the wave, and
$k,{\it\sigma}$
are the wavenumber and frequency of the wave, and
![]() ${\it\epsilon}$
is an amplitude parameter. The mean values of
${\it\epsilon}$
is an amplitude parameter. The mean values of
![]() $k,{\it\sigma},{\it\epsilon}$
over all of the colonies observed were
$k,{\it\sigma},{\it\epsilon}$
over all of the colonies observed were
![]() $k=4.7$
,
$k=4.7$
,
![]() ${\it\sigma}=203~\text{rad}~\text{s}^{-1}$
,
${\it\sigma}=203~\text{rad}~\text{s}^{-1}$
,
![]() ${\it\epsilon}\approx 0.035$
. Such data for each colony measured will make up the full input to our model below.
${\it\epsilon}\approx 0.035$
. Such data for each colony measured will make up the full input to our model below.
1.2 Theoretical background
The model will be an extension to the swirling case of the spherical envelope (or ‘squirmer’) model for the propulsion of ciliated protozoa introduced by Lighthill (Reference Lighthill1952) and Blake (Reference Blake1971b
). When the surface of a cell is densely covered with beating cilia, as for the protist Opalina for example, it is a very good approximation to treat the flow around it as being driven by the displacement of a stretching flexible sheet, attached to the tips of all of the cilia and moving with them. The sheet will undergo radial and tangential wave-like displacements, and it needs to stretch to accommodate temporal variations between the displacements of neighbouring cilia tips (figure 6
a). In the case of Volvox carteri the tips of the beating flagella are not very close together; for a colony of radius
![]() $200~{\rm\mu}\text{m}$
, the average spacing between somatic cells is
$200~{\rm\mu}\text{m}$
, the average spacing between somatic cells is
![]() ${\sim}20~{\rm\mu}\text{m}$
, comparable with the flagellar length,
${\sim}20~{\rm\mu}\text{m}$
, comparable with the flagellar length,
![]() $\langle L\rangle =19.9~{\rm\mu}\text{m}$
(Brumley et al.
Reference Brumley, Wan, Polin and Goldstein2014), so the envelope model may well be somewhat inaccurate. As indicated above, the new feature of our model is the introduction of azimuthal swirl to the envelope model.
$\langle L\rangle =19.9~{\rm\mu}\text{m}$
(Brumley et al.
Reference Brumley, Wan, Polin and Goldstein2014), so the envelope model may well be somewhat inaccurate. As indicated above, the new feature of our model is the introduction of azimuthal swirl to the envelope model.
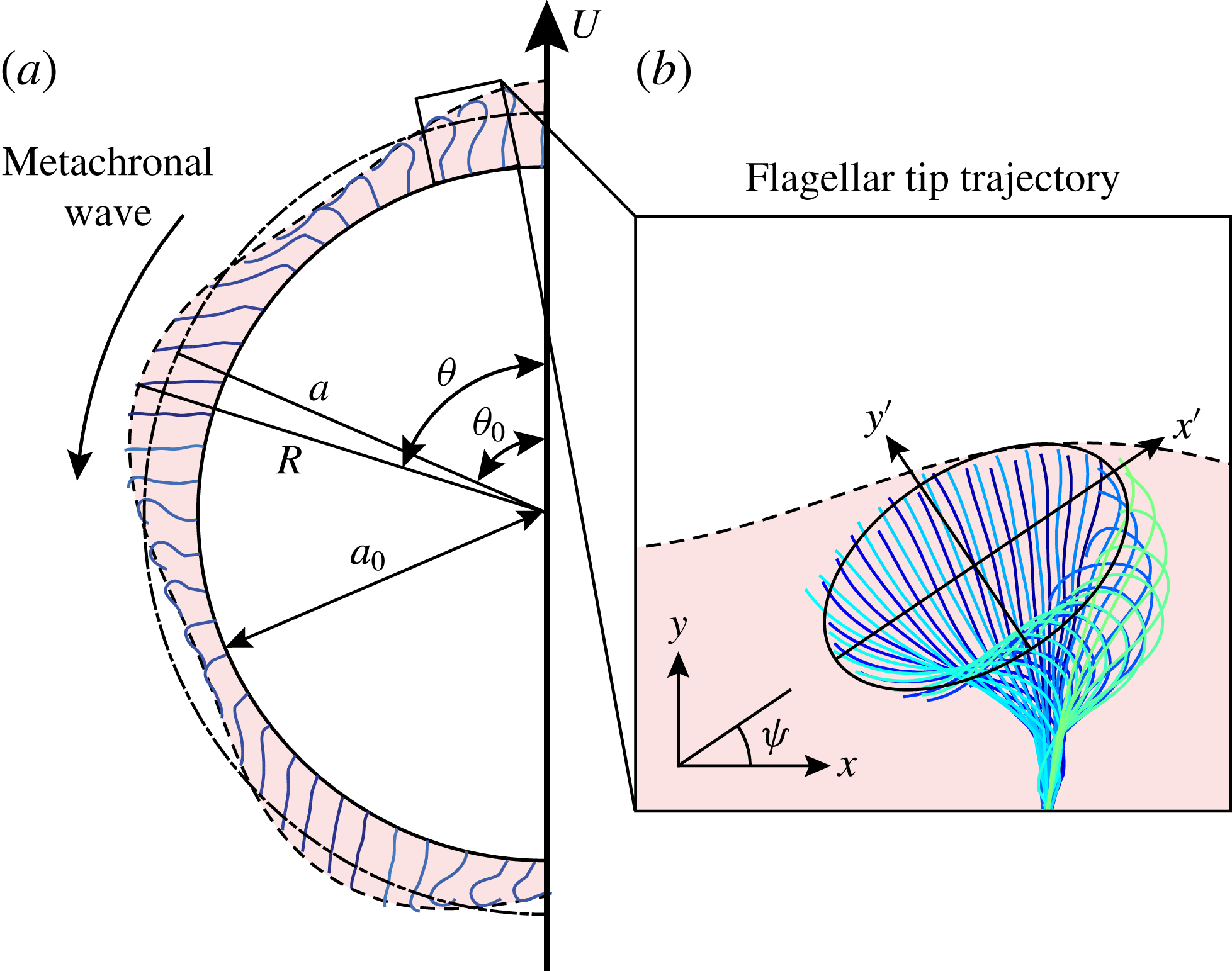
Figure 6. (a) Schematic diagram of a spherical Volvox colony at one instant in time, with beating flagella and the envelope of flagellar tips. The radius of the extracellular matrix in which the flagella are embedded is
![]() $a_{0}$
. The mean radius of the envelope is
$a_{0}$
. The mean radius of the envelope is
![]() $a$
;
$a$
;
![]() $(R,{\it\theta})$
are the coordinates of a surface element whose average position is
$(R,{\it\theta})$
are the coordinates of a surface element whose average position is
![]() $(a,{\it\theta}_{0})$
. (Adapted from Blake (Reference Blake1971b
), but replotted with the experimentally determined metachronal wavenumber.) (b) Measured tip trajectory over multiple beats of a single Volvox flagellum. The trajectory is fitted with an ellipse, which is rotated at an angle
$(a,{\it\theta}_{0})$
. (Adapted from Blake (Reference Blake1971b
), but replotted with the experimentally determined metachronal wavenumber.) (b) Measured tip trajectory over multiple beats of a single Volvox flagellum. The trajectory is fitted with an ellipse, which is rotated at an angle
![]() ${\it\psi}$
with respect to the local colony surface.
${\it\psi}$
with respect to the local colony surface.
The theory will be given in the next two sections, first extending the Lighthill–Blake model to include swirl, and second applying the model to Volvox on the basis of the data of Brumley et al. (Reference Brumley, Polin, Pedley and Goldstein2012). The objective is to calculate the mean swimming speed
![]() $\bar{U}$
and mean angular velocity
$\bar{U}$
and mean angular velocity
![]() $\bar{{\it\Omega}}$
, and test the model by comparison with the measurements of Drescher et al. (Reference Drescher, Leptos, Tuval, Ishikawa, Pedley and Goldstein2009). The final section will include a discussion of discrepancies and the model’s limitations.
$\bar{{\it\Omega}}$
, and test the model by comparison with the measurements of Drescher et al. (Reference Drescher, Leptos, Tuval, Ishikawa, Pedley and Goldstein2009). The final section will include a discussion of discrepancies and the model’s limitations.
2 Theory for squirmers with swirl
In the original, zero-Reynolds-number, spherical-envelope model of ciliated micro-organisms (Lighthill Reference Lighthill1952; Blake Reference Blake1971b
), the radial and tangential Eulerian velocity components
![]() $(u_{r},u_{{\it\theta}})$
are written as infinite series of eigensolutions of the Stokes equation:
$(u_{r},u_{{\it\theta}})$
are written as infinite series of eigensolutions of the Stokes equation:
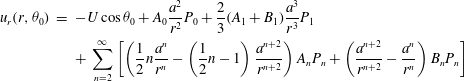 $$\begin{eqnarray}\displaystyle u_{r}(r,{\it\theta}_{0}) & = & \displaystyle -U\cos {\it\theta}_{0}+A_{0}\frac{a^{2}}{r^{2}}P_{0}+\frac{2}{3}(A_{1}+B_{1})\frac{a^{3}}{r^{3}}P_{1}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{n=2}^{\infty }\left[\left(\frac{1}{2}n\frac{a^{n}}{r^{n}}-\left(\frac{1}{2}n-1\right)\frac{a^{n+2}}{r^{n+2}}\right)A_{n}P_{n}+\left(\frac{a^{n+2}}{r^{n+2}}-\frac{a^{n}}{r^{n}}\right)B_{n}P_{n}\right]\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u_{r}(r,{\it\theta}_{0}) & = & \displaystyle -U\cos {\it\theta}_{0}+A_{0}\frac{a^{2}}{r^{2}}P_{0}+\frac{2}{3}(A_{1}+B_{1})\frac{a^{3}}{r^{3}}P_{1}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{n=2}^{\infty }\left[\left(\frac{1}{2}n\frac{a^{n}}{r^{n}}-\left(\frac{1}{2}n-1\right)\frac{a^{n+2}}{r^{n+2}}\right)A_{n}P_{n}+\left(\frac{a^{n+2}}{r^{n+2}}-\frac{a^{n}}{r^{n}}\right)B_{n}P_{n}\right]\end{eqnarray}$$
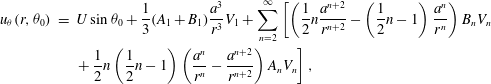 $$\begin{eqnarray}\displaystyle u_{{\it\theta}}(r,{\it\theta}_{0}) & = & \displaystyle U\sin {\it\theta}_{0}+\frac{1}{3}(A_{1}+B_{1})\frac{a^{3}}{r^{3}}V_{1}+\mathop{\sum }_{n=2}^{\infty }\left[\left(\frac{1}{2}n\frac{a^{n+2}}{r^{n+2}}-\left(\frac{1}{2}n-1\right)\frac{a^{n}}{r^{n}}\right)B_{n}V_{n}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{1}{2}n\left(\frac{1}{2}n-1\right)\left(\frac{a^{n}}{r^{n}}-\frac{a^{n+2}}{r^{n+2}}\right)A_{n}V_{n}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u_{{\it\theta}}(r,{\it\theta}_{0}) & = & \displaystyle U\sin {\it\theta}_{0}+\frac{1}{3}(A_{1}+B_{1})\frac{a^{3}}{r^{3}}V_{1}+\mathop{\sum }_{n=2}^{\infty }\left[\left(\frac{1}{2}n\frac{a^{n+2}}{r^{n+2}}-\left(\frac{1}{2}n-1\right)\frac{a^{n}}{r^{n}}\right)B_{n}V_{n}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{1}{2}n\left(\frac{1}{2}n-1\right)\left(\frac{a^{n}}{r^{n}}-\frac{a^{n+2}}{r^{n+2}}\right)A_{n}V_{n}\right],\end{eqnarray}$$
A trace of a typical flagellar beat is shown in figure 6(b), adapted from Brumley et al. (Reference Brumley, Wan, Polin and Goldstein2014), where it can be seen that the trajectory of the tip is approximately elliptical, with centre about two-thirds of the flagellar length from the surface of the extracellular medium. Thus,
![]() $a$
is taken to be the mean radius of a flagellar tip, so we take
$a$
is taken to be the mean radius of a flagellar tip, so we take
![]() $a\approx a_{0}+2L/3$
, where
$a\approx a_{0}+2L/3$
, where
![]() $L$
is the length of a flagellum. With the origin fixed at the centre of the sphere,
$L$
is the length of a flagellum. With the origin fixed at the centre of the sphere,
![]() $-U(t)$
is the speed of the flow at infinity (i.e.
$-U(t)$
is the speed of the flow at infinity (i.e.
![]() $U$
is the instantaneous swimming speed of the sphere). If the sphere is taken to be neutrally buoyant, it experiences no external force, so the Stokeslet term must be zero, and
$U$
is the instantaneous swimming speed of the sphere). If the sphere is taken to be neutrally buoyant, it experiences no external force, so the Stokeslet term must be zero, and
(Blake Reference Blake1971b
). Corresponding to the velocity field (2.1), the velocity components on the sphere
![]() $r=a$
are
$r=a$
are
From this we can see that
![]() $A_{1}$
should be zero, because it corresponds to longitudinal translation of the centre, which is incorporated into
$A_{1}$
should be zero, because it corresponds to longitudinal translation of the centre, which is incorporated into
![]() $U$
. However, we follow Lighthill (Reference Lighthill1952) and not Blake (Reference Blake1971b
) in retaining a non-zero
$U$
. However, we follow Lighthill (Reference Lighthill1952) and not Blake (Reference Blake1971b
) in retaining a non-zero
![]() $A_{0}$
. Blake wished to prohibit any volume change in his squirmers, which is of course physically correct, although if there really were an impenetrable membrane covering the flagellar tips and if, say, all of the flagella beat synchronously, the envelope of their tips would experience a small variation in volume, so
$A_{0}$
. Blake wished to prohibit any volume change in his squirmers, which is of course physically correct, although if there really were an impenetrable membrane covering the flagellar tips and if, say, all of the flagella beat synchronously, the envelope of their tips would experience a small variation in volume, so
![]() $A_{0}$
should not be zero. Our choice of sinusoidal velocity and displacement wave, equations (1.1) and (3.1) below, in fact requires a non-zero
$A_{0}$
should not be zero. Our choice of sinusoidal velocity and displacement wave, equations (1.1) and (3.1) below, in fact requires a non-zero
![]() $A_{0}$
. It turns out that for the parameter values applicable to Volvox the presence or absence of this term makes little difference to the predictions of mean swimming speed, and it does not affect the angular velocity anyway.
$A_{0}$
. It turns out that for the parameter values applicable to Volvox the presence or absence of this term makes little difference to the predictions of mean swimming speed, and it does not affect the angular velocity anyway.
The surface velocities in (2.4) must in fact be generated by the motion of material elements of the spherical envelope, representing the tips of the beating flagella. In the Lighthill–Blake analysis, the envelope is represented by the following expressions for the Lagrangian coordinates
![]() $(R,{\it\theta})$
of the material elements:
$(R,{\it\theta})$
of the material elements:
The new feature that we introduce in this paper is to add axisymmetric swirl velocities and azimuthal (
![]() ${\it\phi}$
) displacements to the above. The
${\it\phi}$
) displacements to the above. The
![]() ${\it\phi}$
component of the Stokes equation is
${\it\phi}$
component of the Stokes equation is
and the general axisymmetric solution that tends to zero at infinity is
equal to
on
![]() $r=a$
. Now the total torque about the axis of symmetry is
$r=a$
. Now the total torque about the axis of symmetry is
![]() $-8{\rm\pi}{\it\mu}a^{3}C_{1}$
and, since the sphere is our model for a free-swimming Volvox colony, this, like the total force, must be zero, i.e.
$-8{\rm\pi}{\it\mu}a^{3}C_{1}$
and, since the sphere is our model for a free-swimming Volvox colony, this, like the total force, must be zero, i.e.
Analogous to (2.5), the
![]() ${\it\phi}$
displacement of the material point
${\it\phi}$
displacement of the material point
![]() $(R,{\it\theta},{\it\phi})$
on the spherical envelope is taken to be
$(R,{\it\theta},{\it\phi})$
on the spherical envelope is taken to be
![]() ${\it\phi}-{\it\phi}_{0}$
where
${\it\phi}-{\it\phi}_{0}$
where
Here
![]() ${\it\phi}_{0}$
is fixed on the rotating sphere, and
${\it\phi}_{0}$
is fixed on the rotating sphere, and
![]() ${\it\Omega}$
is the instantaneous angular velocity of the sphere. The general solution for a squirmer with non-axisymmetric (
${\it\Omega}$
is the instantaneous angular velocity of the sphere. The general solution for a squirmer with non-axisymmetric (
![]() ${\it\phi}$
-dependent) squirming and swirling has been given in terms of vector spherical harmonics by Ghose & Adhikari (Reference Ghose and Adhikari2014), Pak & Lauga (Reference Pak and Lauga2014), Felderhof (Reference Felderhof2016) and Felderhof & Jones (Reference Felderhof and Jones2016). They all calculated the body’s translational and angular velocities corresponding to an arbitrary distribution of velocities on
${\it\phi}$
-dependent) squirming and swirling has been given in terms of vector spherical harmonics by Ghose & Adhikari (Reference Ghose and Adhikari2014), Pak & Lauga (Reference Pak and Lauga2014), Felderhof (Reference Felderhof2016) and Felderhof & Jones (Reference Felderhof and Jones2016). They all calculated the body’s translational and angular velocities corresponding to an arbitrary distribution of velocities on
![]() $r=a$
, but only Felderhof related the surface velocities to Lagrangian displacements of surface elements.
$r=a$
, but only Felderhof related the surface velocities to Lagrangian displacements of surface elements.
The relations between the Eulerian velocities (2.1), (2.7) and the Lagrangian displacements (2.5), (2.10), from which
![]() $A_{n}$
,
$A_{n}$
,
![]() $B_{n}$
,
$B_{n}$
,
![]() $C_{n}$
and
$C_{n}$
and
![]() $U$
,
$U$
,
![]() ${\it\Omega}$
are to be derived from
${\it\Omega}$
are to be derived from
![]() ${\it\alpha}_{n},{\it\beta}_{n},{\it\gamma}_{n}$
, are
${\it\alpha}_{n},{\it\beta}_{n},{\it\gamma}_{n}$
, are
where an overdot represents the time derivative. Blake (Reference Blake1971b
) performed the analysis for the
![]() $r$
and
$r$
and
![]() ${\it\theta}$
velocities; here we illustrate the method by deriving the relation between the
${\it\theta}$
velocities; here we illustrate the method by deriving the relation between the
![]() $C_{n}$
and the
$C_{n}$
and the
![]() ${\it\gamma}_{n}$
.
${\it\gamma}_{n}$
.
The analysis is developed in powers of the amplitude
![]() ${\it\epsilon}$
, so we take
${\it\epsilon}$
, so we take
Immediately, therefore, we see from (2.9) that
![]() ${\it\Omega}^{(1)}=-\dot{{\it\gamma}}_{1}$
, which has zero mean, so the mean angular velocity, like the mean translational speed, is
${\it\Omega}^{(1)}=-\dot{{\it\gamma}}_{1}$
, which has zero mean, so the mean angular velocity, like the mean translational speed, is
![]() $O({\it\epsilon}^{2})$
. At second order, the fact that
$O({\it\epsilon}^{2})$
. At second order, the fact that
![]() $(R,{\it\theta})\neq (a,{\it\theta}_{0})$
is important in the expression for the velocity field:
$(R,{\it\theta})\neq (a,{\it\theta}_{0})$
is important in the expression for the velocity field:
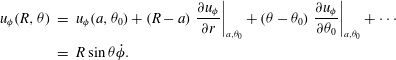 $$\begin{eqnarray}\displaystyle u_{{\it\phi}}(R,{\it\theta}) & = & \displaystyle u_{{\it\phi}}(a,{\it\theta}_{0})+(R-a)\left.\frac{\partial u_{{\it\phi}}}{\partial r}\right|_{a,{\it\theta}_{0}}+({\it\theta}-{\it\theta}_{0})\left.\frac{\partial u_{{\it\phi}}}{\partial {\it\theta}_{0}}\right|_{a,{\it\theta}_{0}}+\cdots \nonumber\\ \displaystyle & = & \displaystyle R\sin {\it\theta}\dot{{\it\phi}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u_{{\it\phi}}(R,{\it\theta}) & = & \displaystyle u_{{\it\phi}}(a,{\it\theta}_{0})+(R-a)\left.\frac{\partial u_{{\it\phi}}}{\partial r}\right|_{a,{\it\theta}_{0}}+({\it\theta}-{\it\theta}_{0})\left.\frac{\partial u_{{\it\phi}}}{\partial {\it\theta}_{0}}\right|_{a,{\it\theta}_{0}}+\cdots \nonumber\\ \displaystyle & = & \displaystyle R\sin {\it\theta}\dot{{\it\phi}}.\end{eqnarray}$$
Substituting for
![]() $R,{\it\theta},{\it\phi}$
gives
$R,{\it\theta},{\it\phi}$
gives
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n=1}^{\infty }({\it\epsilon}C_{n}^{(1)}+{\it\epsilon}^{2}C_{n}^{(2)})V_{n}-{\it\epsilon}^{2}\mathop{\sum }_{n=0}^{\infty }{\it\alpha}_{n}P_{n}\mathop{\sum }_{m=2}^{\infty }(m+1)\dot{{\it\gamma}}_{m}V_{m}\nonumber\\ \displaystyle & & \displaystyle \quad +\,{\it\epsilon}^{2}\mathop{\sum }_{n=1}^{\infty }{\it\beta}_{n}V_{n}\mathop{\sum }_{m=2}^{\infty }\dot{{\it\gamma}}_{m}\left(2P_{m}-\frac{\cos {\it\theta}_{0}}{\sin {\it\theta}_{0}}V_{m}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad ={\it\epsilon}\sin {\it\theta}_{0}\left(1+{\it\epsilon}\mathop{\sum }_{n=0}^{\infty }{\it\alpha}_{n}P_{n}+{\it\epsilon}\frac{\cos {\it\theta}_{0}}{\sin {\it\theta}_{0}}\mathop{\sum }_{n=1}^{\infty }{\it\beta}_{n}V_{n}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\left({\it\Omega}^{(1)}+{\it\epsilon}{\it\Omega}^{(2)}+\frac{1}{\sin {\it\theta}_{0}}\mathop{\sum }_{m=1}^{\infty }\dot{{\it\gamma}}_{m}V_{m}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{n=1}^{\infty }({\it\epsilon}C_{n}^{(1)}+{\it\epsilon}^{2}C_{n}^{(2)})V_{n}-{\it\epsilon}^{2}\mathop{\sum }_{n=0}^{\infty }{\it\alpha}_{n}P_{n}\mathop{\sum }_{m=2}^{\infty }(m+1)\dot{{\it\gamma}}_{m}V_{m}\nonumber\\ \displaystyle & & \displaystyle \quad +\,{\it\epsilon}^{2}\mathop{\sum }_{n=1}^{\infty }{\it\beta}_{n}V_{n}\mathop{\sum }_{m=2}^{\infty }\dot{{\it\gamma}}_{m}\left(2P_{m}-\frac{\cos {\it\theta}_{0}}{\sin {\it\theta}_{0}}V_{m}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad ={\it\epsilon}\sin {\it\theta}_{0}\left(1+{\it\epsilon}\mathop{\sum }_{n=0}^{\infty }{\it\alpha}_{n}P_{n}+{\it\epsilon}\frac{\cos {\it\theta}_{0}}{\sin {\it\theta}_{0}}\mathop{\sum }_{n=1}^{\infty }{\it\beta}_{n}V_{n}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad \times \,\left({\it\Omega}^{(1)}+{\it\epsilon}{\it\Omega}^{(2)}+\frac{1}{\sin {\it\theta}_{0}}\mathop{\sum }_{m=1}^{\infty }\dot{{\it\gamma}}_{m}V_{m}\right).\end{eqnarray}$$
Taking the
![]() $O({\it\epsilon}^{2})$
terms in this equation, multiplying by
$O({\it\epsilon}^{2})$
terms in this equation, multiplying by
![]() $\sin ^{2}{\it\theta}_{0}$
and integrating from
$\sin ^{2}{\it\theta}_{0}$
and integrating from
![]() ${\it\theta}_{0}=0$
to
${\it\theta}_{0}=0$
to
![]() ${\it\theta}_{0}={\rm\pi}$
(recalling that
${\it\theta}_{0}={\rm\pi}$
(recalling that
![]() $C_{1}^{(2)}=0$
), gives the following explicit expression for
$C_{1}^{(2)}=0$
), gives the following explicit expression for
![]() ${\it\Omega}^{(2)}$
:
${\it\Omega}^{(2)}$
:
 $$\begin{eqnarray}\displaystyle {\it\Omega}^{(2)}=-\frac{4}{5}{\it\beta}_{1}\dot{{\it\gamma}}_{2}+\mathop{\sum }_{n=2}^{\infty }\frac{3}{(2n+1)(2n+3)}[-(n+3){\it\alpha}_{n}\dot{{\it\gamma}}_{n+1}+(n+2){\it\alpha}_{n+1}\dot{{\it\gamma}}_{n}] & & \displaystyle \nonumber\\ \displaystyle \quad +\,\mathop{\sum }_{n=2}^{\infty }\frac{6}{(2n+1)(2n+3)(n+1)}[-(n+3){\it\beta}_{n}\dot{{\it\gamma}}_{n+1}+(n-1){\it\beta}_{n+1}\dot{{\it\gamma}}_{n}]. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\Omega}^{(2)}=-\frac{4}{5}{\it\beta}_{1}\dot{{\it\gamma}}_{2}+\mathop{\sum }_{n=2}^{\infty }\frac{3}{(2n+1)(2n+3)}[-(n+3){\it\alpha}_{n}\dot{{\it\gamma}}_{n+1}+(n+2){\it\alpha}_{n+1}\dot{{\it\gamma}}_{n}] & & \displaystyle \nonumber\\ \displaystyle \quad +\,\mathop{\sum }_{n=2}^{\infty }\frac{6}{(2n+1)(2n+3)(n+1)}[-(n+3){\it\beta}_{n}\dot{{\it\gamma}}_{n+1}+(n-1){\it\beta}_{n+1}\dot{{\it\gamma}}_{n}]. & & \displaystyle\end{eqnarray}$$
(Some of the required integrals of products of
![]() $P_{n}$
and
$P_{n}$
and
![]() $V_{m}$
are given in appendix A.) The corresponding result for the second-order term in the translational velocity is
$V_{m}$
are given in appendix A.) The corresponding result for the second-order term in the translational velocity is
 $$\begin{eqnarray}\displaystyle U^{(2)}/a & = & \displaystyle \frac{2}{3}{\it\alpha}_{0}\dot{{\it\beta}}_{1}-\frac{8}{15}{\it\alpha}_{2}\dot{{\it\beta}}_{1}-\frac{2}{5}\dot{{\it\alpha}}_{2}{\it\beta}_{1}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{n=2}^{\infty }\frac{(2n+4){\it\alpha}_{n}\dot{{\it\beta}}_{n+1}-2n\dot{{\it\alpha}}_{n}{\it\beta}_{n+1}-(6n+4){\it\alpha}_{n+1}\dot{{\it\beta}}_{n}-(2n+4)\dot{{\it\alpha}}_{n+1}{\it\beta}_{n}}{(2n+1)(2n+3)}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{n=1}^{\infty }\frac{4(n+2){\it\beta}_{n}\dot{{\it\beta}}_{n+1}-4n\dot{{\it\beta}}_{n}{\it\beta}_{n+1}}{(n+1)(2n+1)(2n+3)}\nonumber\\ \displaystyle & & \displaystyle -\,\mathop{\sum }_{n=2}^{\infty }\frac{(n+1)^{2}{\it\alpha}_{n}\dot{{\it\alpha}}_{n+1}-(n^{2}-4n-2){\it\alpha}_{n+1}\dot{{\it\alpha}}_{n}}{(2n+1)(2n+3)}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle U^{(2)}/a & = & \displaystyle \frac{2}{3}{\it\alpha}_{0}\dot{{\it\beta}}_{1}-\frac{8}{15}{\it\alpha}_{2}\dot{{\it\beta}}_{1}-\frac{2}{5}\dot{{\it\alpha}}_{2}{\it\beta}_{1}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{n=2}^{\infty }\frac{(2n+4){\it\alpha}_{n}\dot{{\it\beta}}_{n+1}-2n\dot{{\it\alpha}}_{n}{\it\beta}_{n+1}-(6n+4){\it\alpha}_{n+1}\dot{{\it\beta}}_{n}-(2n+4)\dot{{\it\alpha}}_{n+1}{\it\beta}_{n}}{(2n+1)(2n+3)}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{n=1}^{\infty }\frac{4(n+2){\it\beta}_{n}\dot{{\it\beta}}_{n+1}-4n\dot{{\it\beta}}_{n}{\it\beta}_{n+1}}{(n+1)(2n+1)(2n+3)}\nonumber\\ \displaystyle & & \displaystyle -\,\mathop{\sum }_{n=2}^{\infty }\frac{(n+1)^{2}{\it\alpha}_{n}\dot{{\it\alpha}}_{n+1}-(n^{2}-4n-2){\it\alpha}_{n+1}\dot{{\it\alpha}}_{n}}{(2n+1)(2n+3)}.\end{eqnarray}$$
This is the formula given by Blake (Reference Blake1971b
), except that he omitted the term involving
![]() ${\it\alpha}_{0}$
which Lighthill (Reference Lighthill1952) included; Lighthill omitted some of the other terms.
${\it\alpha}_{0}$
which Lighthill (Reference Lighthill1952) included; Lighthill omitted some of the other terms.
A shortcut to predicting
![]() $U$
and
$U$
and
![]() ${\it\Omega}$
was proposed by Stone & Samuel (Reference Stone and Samuel1996), following Anderson & Prieve (Reference Anderson and Prieve1991). They used the reciprocal theorem for Stokes flow to relate the translation and rotation speeds of a deformable body with non-zero surface velocity
${\it\Omega}$
was proposed by Stone & Samuel (Reference Stone and Samuel1996), following Anderson & Prieve (Reference Anderson and Prieve1991). They used the reciprocal theorem for Stokes flow to relate the translation and rotation speeds of a deformable body with non-zero surface velocity
![]() $\boldsymbol{u}^{\prime }$
to the drag and torque on a rigid body of instantaneously identical shape, and derived the following results for a sphere of radius
$\boldsymbol{u}^{\prime }$
to the drag and torque on a rigid body of instantaneously identical shape, and derived the following results for a sphere of radius
![]() $a$
, surface
$a$
, surface
![]() $S$
:
$S$
:
3 Application to Volvox
In order to apply the above theory to Volvox, we need to specify the
![]() ${\it\alpha}_{n},{\it\beta}_{n},{\it\gamma}_{n}$
. This will be done by making use of the experimental results on the metachronal wave by Brumley et al. (Reference Brumley, Polin, Pedley and Goldstein2012), which led to (1.1) for the radial velocity distribution on the envelope of flagellar tips, plus assumptions about the tangential and azimuthal displacements. Following (1.1), we write the radial displacement as
${\it\alpha}_{n},{\it\beta}_{n},{\it\gamma}_{n}$
. This will be done by making use of the experimental results on the metachronal wave by Brumley et al. (Reference Brumley, Polin, Pedley and Goldstein2012), which led to (1.1) for the radial velocity distribution on the envelope of flagellar tips, plus assumptions about the tangential and azimuthal displacements. Following (1.1), we write the radial displacement as
where
![]() $k$
is the wavenumber,
$k$
is the wavenumber,
![]() ${\it\sigma}$
the radian frequency, and
${\it\sigma}$
the radian frequency, and
![]() ${\it\epsilon}\ll 1$
. Observations of flagellar beating show that a flagellar tip moves in an approximately elliptical orbit (see figure 6
b). Thus, we may write
${\it\epsilon}\ll 1$
. Observations of flagellar beating show that a flagellar tip moves in an approximately elliptical orbit (see figure 6
b). Thus, we may write
where figure 6(b) suggests
![]() ${\it\delta}\approx 1.68$
and the phase difference
${\it\delta}\approx 1.68$
and the phase difference
![]() ${\it\chi}\approx -{\rm\pi}/2$
. The observation that the plane of beating of the flagella is offset by
${\it\chi}\approx -{\rm\pi}/2$
. The observation that the plane of beating of the flagella is offset by
![]() $10$
–
$10$
–
![]() $20^{\circ }$
from the meridional plane suggests that the functional form of the
$20^{\circ }$
from the meridional plane suggests that the functional form of the
![]() ${\it\phi}$
displacement, relative to the rotating sphere, is also given by (3.2), multiplied by a constant,
${\it\phi}$
displacement, relative to the rotating sphere, is also given by (3.2), multiplied by a constant,
![]() ${\it\tau}$
, equal to the tangent of the offset angle. Together, then, equations (2.5), (2.10), (3.1) and (3.2) give
${\it\tau}$
, equal to the tangent of the offset angle. Together, then, equations (2.5), (2.10), (3.1) and (3.2) give
It can be seen immediately that
![]() ${\it\gamma}_{n}={\it\tau}{\it\beta}_{n}$
, so only (3.3a
) and (3.3b
) need to be solved for
${\it\gamma}_{n}={\it\tau}{\it\beta}_{n}$
, so only (3.3a
) and (3.3b
) need to be solved for
![]() ${\it\alpha}_{n}$
and
${\it\alpha}_{n}$
and
![]() ${\it\beta}_{n}$
. To do this requires expressions for
${\it\beta}_{n}$
. To do this requires expressions for
![]() $\sin k{\it\theta}_{0}$
and
$\sin k{\it\theta}_{0}$
and
![]() $\cos k{\it\theta}_{0}$
as series of both
$\cos k{\it\theta}_{0}$
as series of both
![]() $P_{n}(\cos {\it\theta}_{0})$
and
$P_{n}(\cos {\it\theta}_{0})$
and
![]() $V_{n}(\cos {\it\theta}_{0})$
:
$V_{n}(\cos {\it\theta}_{0})$
:
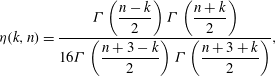 $$\begin{eqnarray}{\it\eta}(k,n)=\frac{{\it\Gamma}\left(\displaystyle \frac{n-k}{2}\right){\it\Gamma}\left(\displaystyle \frac{n+k}{2}\right)}{16{\it\Gamma}\left(\displaystyle \frac{n+3-k}{2}\right){\it\Gamma}\left(\displaystyle \frac{n+3+k}{2}\right)},\end{eqnarray}$$
$$\begin{eqnarray}{\it\eta}(k,n)=\frac{{\it\Gamma}\left(\displaystyle \frac{n-k}{2}\right){\it\Gamma}\left(\displaystyle \frac{n+k}{2}\right)}{16{\it\Gamma}\left(\displaystyle \frac{n+3-k}{2}\right){\it\Gamma}\left(\displaystyle \frac{n+3+k}{2}\right)},\end{eqnarray}$$
and
![]() $k$
is assumed not to be an integer. It then follows from (3.3) that
$k$
is assumed not to be an integer. It then follows from (3.3) that
 $$\begin{eqnarray}\displaystyle {\it\beta}_{n}(t) & = & \displaystyle \frac{{\it\gamma}_{n}}{{\it\tau}}\nonumber\\ \displaystyle & = & \displaystyle \frac{{\it\delta}}{2}(-1)^{n+1}n(n+1)(2n+1)[(-1)^{n}\sin ({\it\sigma}t+{\it\chi})-\sin ({\it\sigma}t+{\it\chi}-k{\rm\pi})]{\it\eta}(k,n).\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\beta}_{n}(t) & = & \displaystyle \frac{{\it\gamma}_{n}}{{\it\tau}}\nonumber\\ \displaystyle & = & \displaystyle \frac{{\it\delta}}{2}(-1)^{n+1}n(n+1)(2n+1)[(-1)^{n}\sin ({\it\sigma}t+{\it\chi})-\sin ({\it\sigma}t+{\it\chi}-k{\rm\pi})]{\it\eta}(k,n).\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Now we can put (3.7) into (2.16) and (2.17), take the mean values and obtain final results for the second-order contributions to the mean angular and translational velocities:
 $$\begin{eqnarray}\displaystyle \bar{{\it\Omega}}^{(2)} & = & \displaystyle 36{\it\sigma}{\it\tau}{\it\delta}^{2}{\it\eta}(k,1){\it\eta}(k,2)\sin k{\rm\pi}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{3}{2}{\it\sigma}{\it\tau}{\it\delta}\sin k{\rm\pi}\mathop{\sum }_{n=2}^{\infty }{\it\eta}(k,n){\it\eta}(k,n+1)(-1)^{n+1}(n+1)(n+2)\nonumber\\ \displaystyle & & \displaystyle \times \,[(2n+3)k\sin {\it\chi}+2{\it\delta}n(n+1)],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \bar{{\it\Omega}}^{(2)} & = & \displaystyle 36{\it\sigma}{\it\tau}{\it\delta}^{2}{\it\eta}(k,1){\it\eta}(k,2)\sin k{\rm\pi}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{3}{2}{\it\sigma}{\it\tau}{\it\delta}\sin k{\rm\pi}\mathop{\sum }_{n=2}^{\infty }{\it\eta}(k,n){\it\eta}(k,n+1)(-1)^{n+1}(n+1)(n+2)\nonumber\\ \displaystyle & & \displaystyle \times \,[(2n+3)k\sin {\it\chi}+2{\it\delta}n(n+1)],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \bar{U}^{(2)} & = & \displaystyle -2a{\it\sigma}{\it\delta}{\it\eta}(k,1){\it\eta}(k,2)\sin k{\rm\pi}\left(12{\it\delta}+\frac{9}{k}\sin {\it\chi}\right)\nonumber\\ \displaystyle & & \displaystyle +\,a{\it\sigma}\sin k{\rm\pi}\mathop{\sum }_{n=2}^{\infty }(-1)^{n}{\it\eta}(k,n){\it\eta}(k,n+1)\nonumber\\ \displaystyle & & \displaystyle \times \,[2{\it\delta}^{2}n(n+1)^{2}(n+2)+2k{\it\delta}(n+1)(2n^{2}+3n+2)\sin {\it\chi}-k^{2}(2n^{2}-2n-1)];\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \bar{U}^{(2)} & = & \displaystyle -2a{\it\sigma}{\it\delta}{\it\eta}(k,1){\it\eta}(k,2)\sin k{\rm\pi}\left(12{\it\delta}+\frac{9}{k}\sin {\it\chi}\right)\nonumber\\ \displaystyle & & \displaystyle +\,a{\it\sigma}\sin k{\rm\pi}\mathop{\sum }_{n=2}^{\infty }(-1)^{n}{\it\eta}(k,n){\it\eta}(k,n+1)\nonumber\\ \displaystyle & & \displaystyle \times \,[2{\it\delta}^{2}n(n+1)^{2}(n+2)+2k{\it\delta}(n+1)(2n^{2}+3n+2)\sin {\it\chi}-k^{2}(2n^{2}-2n-1)];\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
note that non-zero
![]() ${\it\alpha}_{0}$
makes no difference to
${\it\alpha}_{0}$
makes no difference to
![]() $\bar{{\it\Omega}}^{(2)}$
. We may also note that calculations are made easier by recognising that
$\bar{{\it\Omega}}^{(2)}$
. We may also note that calculations are made easier by recognising that
We now put in parameter values obtained from the experiments of Brumley et al. (Reference Brumley, Polin, Pedley and Goldstein2012) and compare the predicted values of
![]() $\bar{U}$
and
$\bar{U}$
and
![]() $\bar{{\it\Omega}}$
with the measurements of Drescher et al. (Reference Drescher, Leptos, Tuval, Ishikawa, Pedley and Goldstein2009). Rather than merely using the average values of
$\bar{{\it\Omega}}$
with the measurements of Drescher et al. (Reference Drescher, Leptos, Tuval, Ishikawa, Pedley and Goldstein2009). Rather than merely using the average values of
![]() $k$
and
$k$
and
![]() ${\it\sigma}$
quoted by Brumley et al. (
${\it\sigma}$
quoted by Brumley et al. (
![]() $k=4.7$
,
$k=4.7$
,
![]() ${\it\sigma}=203~\text{rad}~\text{s}^{-1}$
), we use the individual values for each of the 60 Volvox colonies from which the averages were obtained, together with their radii
${\it\sigma}=203~\text{rad}~\text{s}^{-1}$
), we use the individual values for each of the 60 Volvox colonies from which the averages were obtained, together with their radii
![]() $a$
. We also need the value of the dimensionless amplitude
$a$
. We also need the value of the dimensionless amplitude
![]() ${\it\epsilon}$
. As discussed above, the recorded radius
${\it\epsilon}$
. As discussed above, the recorded radius
![]() $a_{0}$
is the radius of the surface of the extracellular matrix in which the somatic cells are embedded, and
$a_{0}$
is the radius of the surface of the extracellular matrix in which the somatic cells are embedded, and
![]() $a=a_{0}+2L/3$
and, hence,
$a=a_{0}+2L/3$
and, hence,
![]() ${\it\epsilon}=L/(3a_{0}+2L)\approx L/3a_{0}$
(noting the typical orbit in figure 6
b). Solari et al. (Reference Solari, Drescher, Ganguly, Kessler, Michod and Goldstein2011) have shown that flagellar length, as well as colony radius, increases as a colony of V. carteri or V. barberi ages. The values of
${\it\epsilon}=L/(3a_{0}+2L)\approx L/3a_{0}$
(noting the typical orbit in figure 6
b). Solari et al. (Reference Solari, Drescher, Ganguly, Kessler, Michod and Goldstein2011) have shown that flagellar length, as well as colony radius, increases as a colony of V. carteri or V. barberi ages. The values of
![]() $L$
(
$L$
(
![]() $14.9{-}20.5~{\rm\mu}\text{m}$
) and
$14.9{-}20.5~{\rm\mu}\text{m}$
) and
![]() $a_{0}$
quoted by them give values of
$a_{0}$
quoted by them give values of
![]() ${\it\epsilon}$
between 0.029 and 0.038; thus, we may be justified in choosing
${\it\epsilon}$
between 0.029 and 0.038; thus, we may be justified in choosing
![]() ${\it\epsilon}=0.035$
as normal. We also use the value of
${\it\epsilon}=0.035$
as normal. We also use the value of
![]() ${\it\delta}$
(1.68) quoted above, although trajectories of flagellar tips measured by Brumley et al. (Reference Brumley, Wan, Polin and Goldstein2014) show a range of values of
${\it\delta}$
(1.68) quoted above, although trajectories of flagellar tips measured by Brumley et al. (Reference Brumley, Wan, Polin and Goldstein2014) show a range of values of
![]() ${\it\delta}$
from 1.45 to 1.86. Moreover, we use
${\it\delta}$
from 1.45 to 1.86. Moreover, we use
![]() ${\it\tau}=\tan (20^{\circ })\approx 0.36$
although we do not have measurements of the offset angle for individual colonies.
${\it\tau}=\tan (20^{\circ })\approx 0.36$
although we do not have measurements of the offset angle for individual colonies.
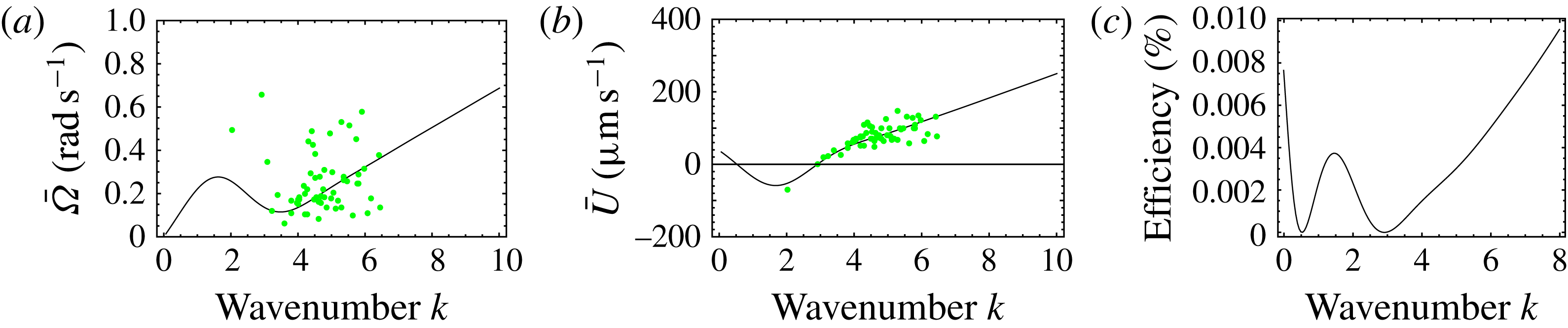
Figure 7. Predicted values of (a) mean angular velocity
![]() $\bar{{\it\Omega}}$
, (b) mean swimming speed
$\bar{{\it\Omega}}$
, (b) mean swimming speed
![]() $\bar{U}$
and (c) mechanical efficiency,
$\bar{U}$
and (c) mechanical efficiency,
![]() $E$
, as functions of the metachronal wavenumber
$E$
, as functions of the metachronal wavenumber
![]() $k$
. Green dots are predictions of the squirmer model using the individually measured parameters for each of the 60 Volvox colonies. The solid lines are the predictions using the mean properties (
$k$
. Green dots are predictions of the squirmer model using the individually measured parameters for each of the 60 Volvox colonies. The solid lines are the predictions using the mean properties (
![]() $k=4.7$
,
$k=4.7$
,
![]() ${\it\sigma}=203~\text{rad}~\text{s}^{-1}$
). Other parameters include
${\it\sigma}=203~\text{rad}~\text{s}^{-1}$
). Other parameters include
![]() ${\it\delta}=1.68$
,
${\it\delta}=1.68$
,
![]() ${\it\chi}=-{\rm\pi}/2$
,
${\it\chi}=-{\rm\pi}/2$
,
![]() ${\it\tau}=\tan (20^{\circ })$
. Here the mean amplitude is
${\it\tau}=\tan (20^{\circ })$
. Here the mean amplitude is
![]() ${\it\epsilon}\approx 0.035$
, equivalent to flagella length
${\it\epsilon}\approx 0.035$
, equivalent to flagella length
![]() $L=20~{\rm\mu}\text{m}$
.
$L=20~{\rm\mu}\text{m}$
.
The results for
![]() $\bar{U}~(={\it\epsilon}^{2}\bar{U}^{(2)})$
and
$\bar{U}~(={\it\epsilon}^{2}\bar{U}^{(2)})$
and
![]() $\bar{{\it\Omega}}~(={\it\epsilon}^{2}\bar{{\it\Omega}}^{(2)})$
are plotted against
$\bar{{\it\Omega}}~(={\it\epsilon}^{2}\bar{{\it\Omega}}^{(2)})$
are plotted against
![]() $k$
in figure 7, where the dots use the individual values of
$k$
in figure 7, where the dots use the individual values of
![]() $k$
,
$k$
,
![]() ${\it\sigma}$
and
${\it\sigma}$
and
![]() $a$
in each of the 60 Volvox colonies measured by Brumley et al. (Reference Brumley, Polin, Pedley and Goldstein2015a
). The continuous curve uses the mean values of
$a$
in each of the 60 Volvox colonies measured by Brumley et al. (Reference Brumley, Polin, Pedley and Goldstein2015a
). The continuous curve uses the mean values of
![]() ${\it\sigma}$
and
${\it\sigma}$
and
![]() $a$
; all results assume a flagellum of length
$a$
; all results assume a flagellum of length
![]() $L=20~{\rm\mu}\text{m}$
, and a mean value of
$L=20~{\rm\mu}\text{m}$
, and a mean value of
![]() ${\it\epsilon}$
of 0.035. It is interesting that
${\it\epsilon}$
of 0.035. It is interesting that
![]() $\bar{U}$
and, to a lesser extent,
$\bar{U}$
and, to a lesser extent,
![]() $\bar{{\it\Omega}}$
increase regularly with
$\bar{{\it\Omega}}$
increase regularly with
![]() $k$
over the range of measured values, but would vary considerably for lower values, even resulting in negative mean swimming speeds.
$k$
over the range of measured values, but would vary considerably for lower values, even resulting in negative mean swimming speeds.
Also plotted, in figure 7(c), is the mechanical efficiency
where
![]() $P$
is the instantaneous rate of working of the stresses at the surface of the sphere,
$P$
is the instantaneous rate of working of the stresses at the surface of the sphere,
and
![]() ${\it\sigma}$
is the stress tensor. The formula for
${\it\sigma}$
is the stress tensor. The formula for
![]() $P$
in the absence of swirl was given by Blake (Reference Blake1971b
, (9)), the additional, third, term due to swirl is equal to
$P$
in the absence of swirl was given by Blake (Reference Blake1971b
, (9)), the additional, third, term due to swirl is equal to
(see also Pak & Lauga Reference Pak and Lauga2014). Figure 7(c) shows a local maximum of
![]() $E$
at
$E$
at
![]() $k\simeq 1.5$
, corresponding to negative swimming speed, which may therefore be discounted. For
$k\simeq 1.5$
, corresponding to negative swimming speed, which may therefore be discounted. For
![]() $k>3.0$
, however, the efficiency increases with
$k>3.0$
, however, the efficiency increases with
![]() $k$
. According to this model, then, it appears that the swimming mode of Volvox did not come about evolutionarily through energetic optimisation.
$k$
. According to this model, then, it appears that the swimming mode of Volvox did not come about evolutionarily through energetic optimisation.
We plot the calculated
![]() $\bar{U}$
and
$\bar{U}$
and
![]() $\bar{{\it\Omega}}$
against
$\bar{{\it\Omega}}$
against
![]() $a$
in figure 8. The green points represent colony-specific predictions using data from Brumley et al. (Reference Brumley, Polin, Pedley and Goldstein2015a
) and the continuous curves correspond to the mean values of
$a$
in figure 8. The green points represent colony-specific predictions using data from Brumley et al. (Reference Brumley, Polin, Pedley and Goldstein2015a
) and the continuous curves correspond to the mean values of
![]() $k$
,
$k$
,
![]() ${\it\sigma}$
and
${\it\sigma}$
and
![]() ${\it\epsilon}$
referred to above. The red points represent the experimental values measured by Drescher et al. (Reference Drescher, Leptos, Tuval, Ishikawa, Pedley and Goldstein2009), again using the individual values of
${\it\epsilon}$
referred to above. The red points represent the experimental values measured by Drescher et al. (Reference Drescher, Leptos, Tuval, Ishikawa, Pedley and Goldstein2009), again using the individual values of
![]() $\bar{U}$
,
$\bar{U}$
,
![]() $\bar{{\it\Omega}}$
and
$\bar{{\it\Omega}}$
and
![]() $a$
for each of the colonies measured (data kindly supplied by Dr Knut Drescher) rather than an average value. As noted in the introduction, with reference to figure 2, because the above theory assumes neutral buoyancy, the value quoted for
$a$
for each of the colonies measured (data kindly supplied by Dr Knut Drescher) rather than an average value. As noted in the introduction, with reference to figure 2, because the above theory assumes neutral buoyancy, the value quoted for
![]() $U$
is the sum of the actual upwards swimming speed
$U$
is the sum of the actual upwards swimming speed
![]() $U_{1}$
and the sedimentation speed
$U_{1}$
and the sedimentation speed
![]() $V$
of an inactive colony of the same radius.
$V$
of an inactive colony of the same radius.
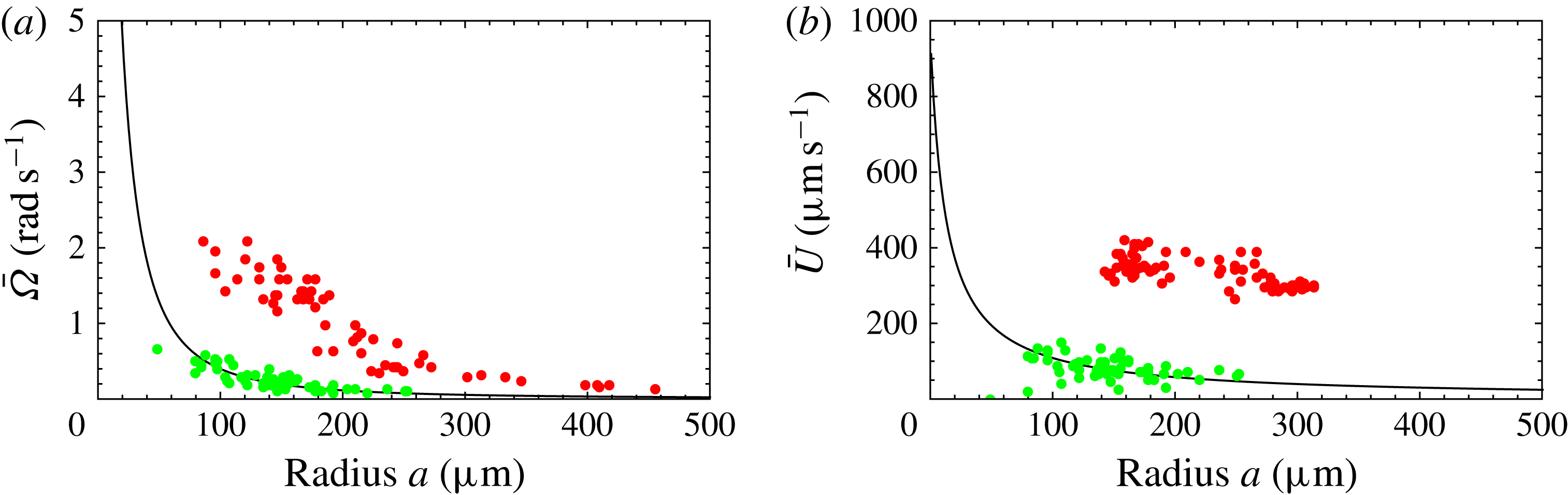
Figure 8. Predicted and measured values of (a) mean angular velocity
![]() $\bar{{\it\Omega}}$
and (b) mean swimming speed
$\bar{{\it\Omega}}$
and (b) mean swimming speed
![]() $\bar{U}$
, as functions of colony radius. Green dots are predictions of this model, red dots are measurements (on a different population of colonies) by Drescher et al. (Reference Drescher, Leptos, Tuval, Ishikawa, Pedley and Goldstein2009) (cf. figure 2). The solid line is the prediction from mean properties of the 60 colonies whose metachronal wave data have been used.
$\bar{U}$
, as functions of colony radius. Green dots are predictions of this model, red dots are measurements (on a different population of colonies) by Drescher et al. (Reference Drescher, Leptos, Tuval, Ishikawa, Pedley and Goldstein2009) (cf. figure 2). The solid line is the prediction from mean properties of the 60 colonies whose metachronal wave data have been used.
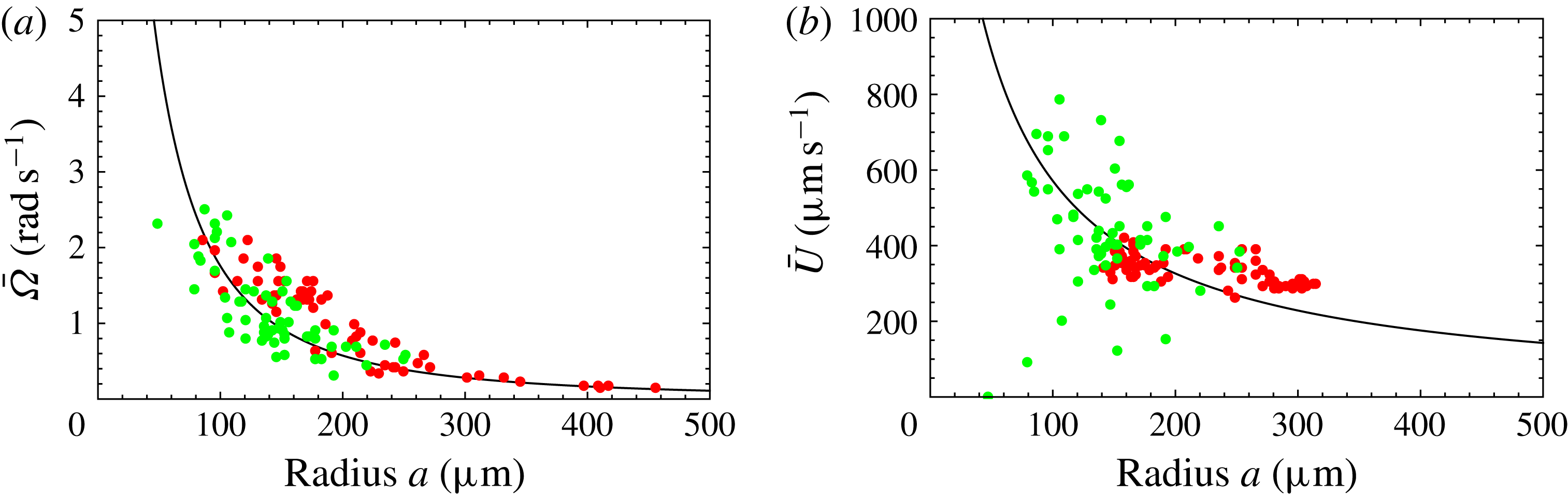
Figure 9. Same as figure 8 but with mean
![]() ${\it\epsilon}\approx 0.10$
(
${\it\epsilon}\approx 0.10$
(
![]() $L=50~{\rm\mu}\text{m}$
).
$L=50~{\rm\mu}\text{m}$
).

Figure 10. Squirming flow fields. Radial (a) and tangential (b) components of the fluid velocity field shown at various times through one flagellar beating cycle. The metachronal wave properties ((3.1) and (3.2)) are the same as for the average Volvox colony (
![]() $k=4.7$
,
$k=4.7$
,
![]() ${\it\sigma}=203~\text{rad}~\text{s}^{-1}$
,
${\it\sigma}=203~\text{rad}~\text{s}^{-1}$
,
![]() $a_{0}=144~{\rm\mu}\text{m}$
) and other parameters correspond to measured flagella and their trajectories (
$a_{0}=144~{\rm\mu}\text{m}$
) and other parameters correspond to measured flagella and their trajectories (
![]() $L=20~{\rm\mu}\text{m}$
,
$L=20~{\rm\mu}\text{m}$
,
![]() ${\it\delta}=1.68$
,
${\it\delta}=1.68$
,
![]() ${\it\chi}=-{\rm\pi}/2$
).
${\it\chi}=-{\rm\pi}/2$
).
In figure 8, the predictions for both
![]() $\bar{U}$
and
$\bar{U}$
and
![]() $\bar{{\it\Omega}}$
are significantly below the measured values, though the trend with increasing radius is similar. If we had taken the flagellar length
$\bar{{\it\Omega}}$
are significantly below the measured values, though the trend with increasing radius is similar. If we had taken the flagellar length
![]() $L$
to be
$L$
to be
![]() $50~{\rm\mu}\text{m}$
instead of
$50~{\rm\mu}\text{m}$
instead of
![]() $20~{\rm\mu}\text{m}$
, the agreement would seem to be almost perfect (figure 9). In the next section we discuss in more detail aspects of the model that may need to be improved.
$20~{\rm\mu}\text{m}$
, the agreement would seem to be almost perfect (figure 9). In the next section we discuss in more detail aspects of the model that may need to be improved.
In addition to calculating
![]() $\bar{{\it\Omega}}$
and
$\bar{{\it\Omega}}$
and
![]() $\bar{U}$
we can use the squirmer model to compute the time-dependent velocity field, for comparison with the measurements in figures 4 and 5. Figure 10 shows the radial and tangential velocities as functions of position at different times during a cycle, for the mean values of
$\bar{U}$
we can use the squirmer model to compute the time-dependent velocity field, for comparison with the measurements in figures 4 and 5. Figure 10 shows the radial and tangential velocities as functions of position at different times during a cycle, for the mean values of
![]() $k$
(4.7),
$k$
(4.7),
![]() ${\it\sigma}$
(203 rad s
${\it\sigma}$
(203 rad s
![]() $^{-1}$
) and
$^{-1}$
) and
![]() $a_{0}=144~{\rm\mu}\text{m}$
. Both velocity components show the metachronal wave, which is not surprising since that was used as input from (3.1) and (3.2). The figure also indicates that the tangential velocity component decays more rapidly with radial distance than the radial component. Calculated kymographs of
$a_{0}=144~{\rm\mu}\text{m}$
. Both velocity components show the metachronal wave, which is not surprising since that was used as input from (3.1) and (3.2). The figure also indicates that the tangential velocity component decays more rapidly with radial distance than the radial component. Calculated kymographs of
![]() $u_{r}$
and
$u_{r}$
and
![]() $u_{{\it\theta}}$
at
$u_{{\it\theta}}$
at
![]() $r=1.3\times a_{0}$
are shown in figure 11, and can be compared with figure 5. There is good qualitative agreement between figures 10 and 11 and figures 4 and 5. Unlike the mean velocity, however, which is lower than measured, the amplitude of the calculated
$r=1.3\times a_{0}$
are shown in figure 11, and can be compared with figure 5. There is good qualitative agreement between figures 10 and 11 and figures 4 and 5. Unlike the mean velocity, however, which is lower than measured, the amplitude of the calculated
![]() $u_{r}$
or
$u_{r}$
or
![]() $u_{{\it\theta}}$
oscillations, scaling as
$u_{{\it\theta}}$
oscillations, scaling as
![]() ${\it\sigma}a_{0}{\it\epsilon}$
from (2.11a-c
) and (3.1), is about
${\it\sigma}a_{0}{\it\epsilon}$
from (2.11a-c
) and (3.1), is about
![]() $1000~{\rm\mu}\text{m}~\text{s}^{-1}$
, significantly larger than the measured value of about
$1000~{\rm\mu}\text{m}~\text{s}^{-1}$
, significantly larger than the measured value of about
![]() $300~{\rm\mu}\text{m}~\text{s}^{-1}$
(figure 5).
$300~{\rm\mu}\text{m}~\text{s}^{-1}$
(figure 5).

Figure 11. Squirmer kymographs. Radial
![]() $u_{r}$
(a) and tangential
$u_{r}$
(a) and tangential
![]() $u_{{\it\theta}}$
(b) components of the flow, as functions of polar angle
$u_{{\it\theta}}$
(b) components of the flow, as functions of polar angle
![]() ${\it\theta}$
and time
${\it\theta}$
and time
![]() $t$
, computed at the fixed radius (
$t$
, computed at the fixed radius (
![]() $r=1.3\times a_{0}$
). Other parameters are the same as in figure 10.
$r=1.3\times a_{0}$
). Other parameters are the same as in figure 10.
4 Discussion
The main discrepancy between the theoretical predictions of this paper and the experimental observations of Drescher et al. (Reference Drescher, Leptos, Tuval, Ishikawa, Pedley and Goldstein2009) is that, although the maximum fluid velocity during a cycle, for the experimental parameter values, is much larger in the model than measured, the predicted mean velocity and angular velocity are significantly smaller than measured.
The envelope model is clearly a great oversimplification, because even in the context of single-celled ciliates, the cilia tips do not form a continuous surface at all times. Not only may there be wide spaces between neighbouring tips, but also some tips may, during their recovery stroke, be overshadowed by others in their power stroke, so the envelope is not single-valued (Brennen & Winet Reference Brennen and Winet1977). The latter is not a problem for V. carteri, because the flagellar pairs are more widely spaced, but that in itself adds to the former difficulty. Blake (Reference Blake1971b ) argued that the envelope model would be a better approximation for symplectic metachronal waves than for antiplectic ones, because the tips are closer together during the power stroke, when their effect on the neighbouring fluid is greatest; this is especially true for a ciliate such as Opalina, but is less compelling in the case of V. carteri, for which typical cell (and, hence, flagellar) spacings are roughly equal to the flagellar length. The wide spacing between flagellar tips means that much of the ‘envelope’ is not actively engaged in driving fluid past the surface, and fluid can leak back between neighbours, so one would expect the model to overestimate the fluid velocity, as it does if one considers the maximum instantaneous radial or tangential velocity. As reviewed elsewhere (Goldstein Reference Goldstein2015), the volvocine algae include a range of species with differing interflagellar distances, some of which are significantly smaller than in V. carteri, and one can anticipate that future studies of those species may shed further light on the validity of the envelope model.
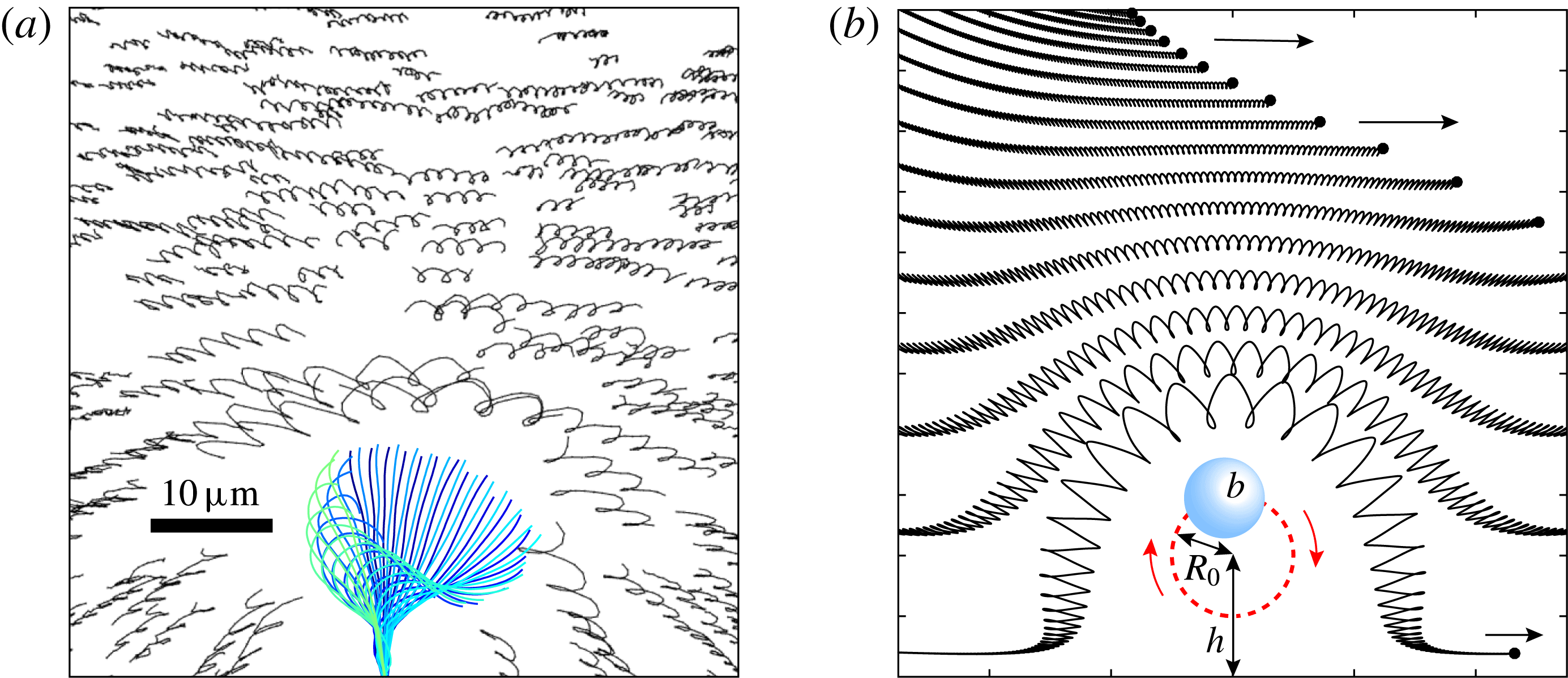
Figure 12. Particle paths in the vicinity of a flagellum. (a) Trajectories of
![]() $0.5~{\rm\mu}\text{m}$
passive tracers near an isolated Volvox flagellum held with a glass micropipette. The tracked flagellar waveform from several beats is also shown. (b) A sphere of radius
$0.5~{\rm\mu}\text{m}$
passive tracers near an isolated Volvox flagellum held with a glass micropipette. The tracked flagellar waveform from several beats is also shown. (b) A sphere of radius
![]() $b$
moving in a circular trajectory above and perpendicular to a no-slip boundary produces a time-dependent flow, which closely mimics that of a real flagellum. This simulation of 100 beats shows particle paths from various initial positions, and corresponds to
$b$
moving in a circular trajectory above and perpendicular to a no-slip boundary produces a time-dependent flow, which closely mimics that of a real flagellum. This simulation of 100 beats shows particle paths from various initial positions, and corresponds to
![]() $h=10~{\rm\mu}\text{m}$
,
$h=10~{\rm\mu}\text{m}$
,
![]() $R_{0}=5~{\rm\mu}\text{m}$
,
$R_{0}=5~{\rm\mu}\text{m}$
,
![]() $b=5~{\rm\mu}\text{m}$
.
$b=5~{\rm\mu}\text{m}$
.
Why, therefore, is the mean velocity underestimated? It seems likely that the difference lies in the fact that each flagellum beats close to the no-slip surface of the extracellular matrix in which the somatic cells are embedded. In the power stroke, a flagellum is extended and its outer parts, in particular the tip, set neighbouring fluid particles in motion, over a range of several flagellar radii, at about the same speed as the tip. During the recovery stroke, on the other hand, the flagellum is much more curved, and the outer part remains roughly parallel to the colony surface (Blake Reference Blake1972). Thus the drag exerted by the outer part of the flagellum on the fluid will be reduced by a factor approaching two compared with the power stroke. Moreover, this outer part is relatively close to the colony surface, and the no-slip condition on that surface will prevent fluid particles from moving at the same speed as the tip except very close to it. Both these factors mean that, although every element of the beating flagellum oscillates with zero mean displacement, the fluid velocities that it generates do not have zero mean.
As part of the experiments reported by Brumley et al. (Reference Brumley, Wan, Polin and Goldstein2014), movies were taken of the motion of microspheres in the flow driven by a single beating flagellum on an isolated V. carteri somatic cell fixed on a micropipette. Experimental details are given briefly in appendix C. One of these movies is reproduced in movie S3, in which the difference between the fluid particle displacements in power and recovery strokes can be clearly seen. The trajectories of a number of the microspheres are shown in figure 12(a). Movie S4 and figure 12(b) show particle trajectories calculated from a very simple model (see appendix C), which consists of a small spherical bead following a circular orbit perpendicular to a nearby rigid plane (such an orbiting bead model of a beating flagellum has been used extensively in recent years (Lenz & Ryskin Reference Lenz and Ryskin2006; Vilfan & Jülicher Reference Vilfan and Jülicher2006; Niedermayer et al. Reference Niedermayer, Eckhardt and Lenz2008; Uchida & Golestanian Reference Uchida and Golestanian2011; Brumley et al. Reference Brumley, Polin, Pedley and Goldstein2012, Reference Brumley, Polin, Pedley and Goldstein2015a ; Bruot & Cicuta Reference Bruot and Cicuta2016)). The similarity between the measured and computed trajectories is clear.
It is therefore evident that the net tangential velocity excess of the power stroke over the recovery stroke of Volvox flagella will be
![]() $O({\it\epsilon})$
, so the mean velocity generated will be
$O({\it\epsilon})$
, so the mean velocity generated will be
![]() $O({\it\epsilon})$
not
$O({\it\epsilon})$
not
![]() $O({\it\epsilon}^{2})$
as obtained from our squirmer model. That may be a more important limitation of the model than the wide spacing of the flagella. What is required, in future, is a detailed fluid dynamic analysis of an array of beating flagella on the surface of a sphere. This will be an extension of the so-called sublayer model of Blake (Reference Blake1972) and Brennen & Winet (Reference Brennen and Winet1977), in which each cilium is represented as a linear distribution of Stokeslets whose strengths can be estimated using resistive force theory, or calculated more accurately as the solution of an integral equation using slender-body theory, taking account of the no-slip boundary by including the Stokeslet image system as derived for a planar boundary by Blake (Reference Blake1971a
). This model is currently being developed.
$O({\it\epsilon}^{2})$
as obtained from our squirmer model. That may be a more important limitation of the model than the wide spacing of the flagella. What is required, in future, is a detailed fluid dynamic analysis of an array of beating flagella on the surface of a sphere. This will be an extension of the so-called sublayer model of Blake (Reference Blake1972) and Brennen & Winet (Reference Brennen and Winet1977), in which each cilium is represented as a linear distribution of Stokeslets whose strengths can be estimated using resistive force theory, or calculated more accurately as the solution of an integral equation using slender-body theory, taking account of the no-slip boundary by including the Stokeslet image system as derived for a planar boundary by Blake (Reference Blake1971a
). This model is currently being developed.
Three other assumptions in the theory of this paper should be discussed. First is the choice of a sine wave to represent the displacement of the flagella tips ((3.1) and (3.2)). The choice necessitates some intricate calculations (§ 3 and appendix B) and it could be argued that the measurements of Brumley et al. (Reference Brumley, Polin, Pedley and Goldstein2012) are not sufficiently refined to justify it. Blake (Reference Blake1971b
), among others, proposed that four terms in the Legendre polynomial expansions (2.4) would be accurate enough. Moreover, that would avoid the problem of non-zero values for
![]() $A_{0}$
and
$A_{0}$
and
![]() ${\it\alpha}_{0}$
. However, a sine wave still seems the most natural choice for a propagating wave, and we have assumed it accordingly.
${\it\alpha}_{0}$
. However, a sine wave still seems the most natural choice for a propagating wave, and we have assumed it accordingly.
Another choice made here is to truncate the expansions of derived quantities at
![]() $O({\it\epsilon}^{2})$
, which is likely to lead to errors at larger values of
$O({\it\epsilon}^{2})$
, which is likely to lead to errors at larger values of
![]() ${\it\epsilon}$
(Drummond Reference Drummond1966); however, even for figure 9, the assumed value of
${\it\epsilon}$
(Drummond Reference Drummond1966); however, even for figure 9, the assumed value of
![]() ${\it\epsilon}$
was less than 0.1, so this is unlikely to cause a significant error in figure 8. A third assumption in this paper is that the elliptical trajectory of each flagellar tip has its major axis parallel to the locally planar no-slip colony surface. In fact, it will in general be at a non-zero angle
${\it\epsilon}$
was less than 0.1, so this is unlikely to cause a significant error in figure 8. A third assumption in this paper is that the elliptical trajectory of each flagellar tip has its major axis parallel to the locally planar no-slip colony surface. In fact, it will in general be at a non-zero angle
![]() ${\it\psi}$
to that surface (figure 6
b). In that case the calculation becomes somewhat more cumbersome but no more difficult, as outlined in appendix D. If we choose
${\it\psi}$
to that surface (figure 6
b). In that case the calculation becomes somewhat more cumbersome but no more difficult, as outlined in appendix D. If we choose
![]() ${\it\psi}=30^{\circ }$
, for example, the results for
${\it\psi}=30^{\circ }$
, for example, the results for
![]() $\bar{U}$
and
$\bar{U}$
and
![]() $\bar{{\it\Omega}}$
are negligibly different from those in figure 8. The assumption that
$\bar{{\it\Omega}}$
are negligibly different from those in figure 8. The assumption that
![]() ${\it\psi}=0$
is therefore not responsible for the discrepancy between theory and experiment in that figure.
${\it\psi}=0$
is therefore not responsible for the discrepancy between theory and experiment in that figure.
Acknowledgements
The authors are very grateful to Dr K. Drescher, for the use of his original data in figure 8, Dr K.Y. Wan, for her data in figure 6(b), and Dr T. Montenegro-Johnson, for enlightening discussions on the future development of a complete sublayer model of Volvox swimming. We would also like to express our warm thanks to Professor John Blake for his careful reading of our manuscript and suggestions for its improvement. This work was supported by a Human Frontier Science Program Cross-Disciplinary Fellowship (D.R.B.) and a Senior Investigator Award from the Wellcome Trust (R.E.G.).
Supplementary movies
Supplementary movies are available at http://dx.doi.org/10.1017/jfm.2016.306.
Appendix A. Integrals required in the derivation of (2.16)
We seek to evaluate
and
where
![]() $V_{n}$
is defined by (2.2), using the standard recurrence relations and differential equation for Legendre polynomials:
$V_{n}$
is defined by (2.2), using the standard recurrence relations and differential equation for Legendre polynomials:
where
Hence,
From (A 2),
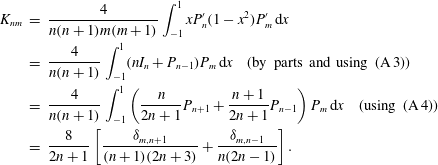 $$\begin{eqnarray}\displaystyle K_{nm} & = & \displaystyle \frac{4}{n(n+1)m(m+1)}\int _{-1}^{1}xP_{n}^{\prime }(1-x^{2})P_{m}^{\prime }\,\text{d}x\nonumber\\ \displaystyle & = & \displaystyle \frac{4}{n(n+1)}\int _{-1}^{1}(nI_{n}+P_{n-1})P_{m}\,\text{d}x\quad \text{(by parts and using (A 3))}\nonumber\\ \displaystyle & = & \displaystyle \frac{4}{n(n+1)}\int _{-1}^{1}\left(\frac{n}{2n+1}P_{n+1}+\frac{n+1}{2n+1}P_{n-1}\right)P_{m}\,\text{d}x\quad \text{(using (A 4))}\nonumber\\ \displaystyle & = & \displaystyle \frac{8}{2n+1}\left[\frac{{\it\delta}_{m,n+1}}{(n+1)(2n+3)}+\frac{{\it\delta}_{m,n-1}}{n(2n-1)}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{nm} & = & \displaystyle \frac{4}{n(n+1)m(m+1)}\int _{-1}^{1}xP_{n}^{\prime }(1-x^{2})P_{m}^{\prime }\,\text{d}x\nonumber\\ \displaystyle & = & \displaystyle \frac{4}{n(n+1)}\int _{-1}^{1}(nI_{n}+P_{n-1})P_{m}\,\text{d}x\quad \text{(by parts and using (A 3))}\nonumber\\ \displaystyle & = & \displaystyle \frac{4}{n(n+1)}\int _{-1}^{1}\left(\frac{n}{2n+1}P_{n+1}+\frac{n+1}{2n+1}P_{n-1}\right)P_{m}\,\text{d}x\quad \text{(using (A 4))}\nonumber\\ \displaystyle & = & \displaystyle \frac{8}{2n+1}\left[\frac{{\it\delta}_{m,n+1}}{(n+1)(2n+3)}+\frac{{\it\delta}_{m,n-1}}{n(2n-1)}\right].\end{eqnarray}$$
Appendix B. Proof of (3.5a )
We prove by induction the first of the formulae in (3.5); proofs of the others are similar. Let
so that
from the first of (3.4a ). The result we seek to prove is
where
![]() ${\it\eta}(k,n)$
is given by (3.6). From (B 1) and (A 4), we have
${\it\eta}(k,n)$
is given by (3.6). From (B 1) and (A 4), we have
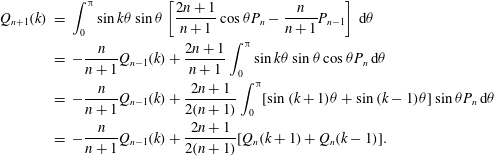 $$\begin{eqnarray}\displaystyle Q_{n+1}(k) & = & \displaystyle \int _{0}^{{\rm\pi}}\sin k{\it\theta}\sin {\it\theta}\left[\frac{2n+1}{n+1}\cos {\it\theta}P_{n}-\frac{n}{n+1}P_{n-1}\right]\,\text{d}{\it\theta}\nonumber\\ \displaystyle & = & \displaystyle -\frac{n}{n+1}Q_{n-1}(k)+\frac{2n+1}{n+1}\int _{0}^{{\rm\pi}}\sin k{\it\theta}\sin {\it\theta}\cos {\it\theta}P_{n}\,\text{d}{\it\theta}\nonumber\\ \displaystyle & = & \displaystyle -\frac{n}{n+1}Q_{n-1}(k)+\frac{2n+1}{2(n+1)}\int _{0}^{{\rm\pi}}[\sin (k+1){\it\theta}+\sin (k-1){\it\theta}]\sin {\it\theta}P_{n}\,\text{d}{\it\theta}\nonumber\\ \displaystyle & = & \displaystyle -\frac{n}{n+1}Q_{n-1}(k)+\frac{2n+1}{2(n+1)}[Q_{n}(k+1)+Q_{n}(k-1)].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Q_{n+1}(k) & = & \displaystyle \int _{0}^{{\rm\pi}}\sin k{\it\theta}\sin {\it\theta}\left[\frac{2n+1}{n+1}\cos {\it\theta}P_{n}-\frac{n}{n+1}P_{n-1}\right]\,\text{d}{\it\theta}\nonumber\\ \displaystyle & = & \displaystyle -\frac{n}{n+1}Q_{n-1}(k)+\frac{2n+1}{n+1}\int _{0}^{{\rm\pi}}\sin k{\it\theta}\sin {\it\theta}\cos {\it\theta}P_{n}\,\text{d}{\it\theta}\nonumber\\ \displaystyle & = & \displaystyle -\frac{n}{n+1}Q_{n-1}(k)+\frac{2n+1}{2(n+1)}\int _{0}^{{\rm\pi}}[\sin (k+1){\it\theta}+\sin (k-1){\it\theta}]\sin {\it\theta}P_{n}\,\text{d}{\it\theta}\nonumber\\ \displaystyle & = & \displaystyle -\frac{n}{n+1}Q_{n-1}(k)+\frac{2n+1}{2(n+1)}[Q_{n}(k+1)+Q_{n}(k-1)].\end{eqnarray}$$
Now suppose that (B 3) is true for
![]() $Q_{n-1}$
and
$Q_{n-1}$
and
![]() $Q_{n}$
, for all
$Q_{n}$
, for all
![]() $k$
, substitute it into the right-hand side of (B 4), and after some algebra indeed obtain (B 3) with
$k$
, substitute it into the right-hand side of (B 4), and after some algebra indeed obtain (B 3) with
![]() $n$
replaced by
$n$
replaced by
![]() $n+1$
. The induction can be shown to start, with
$n+1$
. The induction can be shown to start, with
![]() $n=1$
and
$n=1$
and
![]() $n=2$
, using the standard identities
$n=2$
, using the standard identities
Appendix C. Flagellar flow fields
To investigate the time-dependent flow fields produced by individual eukaryotic flagella, Brumley et al. (Reference Brumley, Wan, Polin and Goldstein2014) isolated individual cells from colonies of V. carteri, captured and oriented them using glass micropipettes, and imaged the motion of
![]() $0.5~{\rm\mu}\text{m}$
polystyrene microspheres within the fluid at 1000 f.p.s. One such movie is included as movie S3, which shows the time-dependent motion of these passive tracers in the vicinity of the beating flagellum. Using custom-made tracking routines, we identify the trajectories of the microspheres, and these are shown in figure 12(a), together with the tracked flagellar waveform over several beats. Tracer particles in the immediate vicinity of the flagellar tip exhibit very little back flow during the recovery stroke.
$0.5~{\rm\mu}\text{m}$
polystyrene microspheres within the fluid at 1000 f.p.s. One such movie is included as movie S3, which shows the time-dependent motion of these passive tracers in the vicinity of the beating flagellum. Using custom-made tracking routines, we identify the trajectories of the microspheres, and these are shown in figure 12(a), together with the tracked flagellar waveform over several beats. Tracer particles in the immediate vicinity of the flagellar tip exhibit very little back flow during the recovery stroke.
We consider now the flow field produced by a simple model flagellum, which consists of a sphere of radius
![]() $b$
driven at a constant angular speed
$b$
driven at a constant angular speed
![]() ${\it\omega}$
around a circular trajectory of radius
${\it\omega}$
around a circular trajectory of radius
![]() $R_{0}$
, perpendicular to an infinite no-slip boundary. The trajectory of the sphere is given by
$R_{0}$
, perpendicular to an infinite no-slip boundary. The trajectory of the sphere is given by
where
![]() $\boldsymbol{x}_{0}=h\hat{\boldsymbol{z}}$
. The velocity of the particle is then
$\boldsymbol{x}_{0}=h\hat{\boldsymbol{z}}$
. The velocity of the particle is then
The force that this particle imparts on the fluid is given by
We know that
![]() $z(t)=h+R_{0}\cos {\it\omega}t$
, and therefore the time-dependent force exerted on the fluid is
$z(t)=h+R_{0}\cos {\it\omega}t$
, and therefore the time-dependent force exerted on the fluid is
The fluid velocity
![]() $\boldsymbol{u}(\boldsymbol{x})$
at position
$\boldsymbol{u}(\boldsymbol{x})$
at position
![]() $\boldsymbol{x}$
is expressed in terms of the Green’s function in the presence of the no-slip boundary condition (Blake Reference Blake1971a
):
$\boldsymbol{x}$
is expressed in terms of the Green’s function in the presence of the no-slip boundary condition (Blake Reference Blake1971a
):
where
and
Numerical solutions of (C 10) are shown in figure 12(b) for various initial positions. The parameters used are designed to mimic those of real Volvox flagella (
![]() $h=10~{\rm\mu}\text{m}$
,
$h=10~{\rm\mu}\text{m}$
,
![]() $R_{0}=5~{\rm\mu}\text{m}$
). A sphere of radius
$R_{0}=5~{\rm\mu}\text{m}$
). A sphere of radius
![]() $b=5~{\rm\mu}\text{m}$
is used, though we emphasise that strictly speaking this does not come into contact with the plane. The finite value of
$b=5~{\rm\mu}\text{m}$
is used, though we emphasise that strictly speaking this does not come into contact with the plane. The finite value of
![]() $b$
is used simply to generate variable drag as a function of height, in order to produce a net flow. In addition, the particle trajectories are independent of the speed of the sphere, and so the results in figure 12(b) would be unchanged if the sphere were instead driven by either a constant force, or by a phase-dependent term.
$b$
is used simply to generate variable drag as a function of height, in order to produce a net flow. In addition, the particle trajectories are independent of the speed of the sphere, and so the results in figure 12(b) would be unchanged if the sphere were instead driven by either a constant force, or by a phase-dependent term.
Appendix D. Rotated ellipse
In this section, we consider the case in which the elliptical trajectory of the flagellar tip is rotated at an angle
![]() ${\it\psi}$
with respect to the surface of the Volvox colony. In this case, (3.1) and (3.2) can be generalised to become
${\it\psi}$
with respect to the surface of the Volvox colony. In this case, (3.1) and (3.2) can be generalised to become
 $$\begin{eqnarray}\displaystyle \bar{{\it\Omega}}^{(2)} & = & \displaystyle 18{\it\sigma}{\it\tau}{\it\eta}(k,1){\it\eta}(k,2)\sin k{\rm\pi}[({\it\delta}^{2}-1)\cos 2{\it\psi}+1+{\it\delta}^{2}+2{\it\delta}\cos {\it\chi}\sin 2{\it\psi}]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{3}{2}{\it\sigma}{\it\tau}\sin k{\rm\pi}\mathop{\sum }_{n=2}^{\infty }{\it\eta}(k,n){\it\eta}(k,n+1)(-1)^{n+1}(n+1)(n+2)\nonumber\\ \displaystyle & & \displaystyle \times \,[n(n+1)({\it\delta}^{2}-1)\cos 2{\it\psi}+k(2n+3){\it\delta}\sin {\it\chi}\nonumber\\ \displaystyle & & \displaystyle +\,n(n+1)(1+{\it\delta}^{2}+2{\it\delta}\cos {\it\chi}\sin 2{\it\psi})],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \bar{{\it\Omega}}^{(2)} & = & \displaystyle 18{\it\sigma}{\it\tau}{\it\eta}(k,1){\it\eta}(k,2)\sin k{\rm\pi}[({\it\delta}^{2}-1)\cos 2{\it\psi}+1+{\it\delta}^{2}+2{\it\delta}\cos {\it\chi}\sin 2{\it\psi}]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{3}{2}{\it\sigma}{\it\tau}\sin k{\rm\pi}\mathop{\sum }_{n=2}^{\infty }{\it\eta}(k,n){\it\eta}(k,n+1)(-1)^{n+1}(n+1)(n+2)\nonumber\\ \displaystyle & & \displaystyle \times \,[n(n+1)({\it\delta}^{2}-1)\cos 2{\it\psi}+k(2n+3){\it\delta}\sin {\it\chi}\nonumber\\ \displaystyle & & \displaystyle +\,n(n+1)(1+{\it\delta}^{2}+2{\it\delta}\cos {\it\chi}\sin 2{\it\psi})],\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle \bar{U}^{(2)} & = & \displaystyle -6a{\it\sigma}{\it\eta}(k,1){\it\eta}(k,2)\sin k{\rm\pi}\nonumber\\ \displaystyle & & \displaystyle \times \,\left[\frac{3{\it\delta}\sin {\it\chi}}{k}+2({\it\delta}^{2}+2{\it\delta}\cos {\it\chi}\sin 2{\it\psi}+1)+2({\it\delta}^{2}-1)\cos 2{\it\psi}\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2}a{\it\sigma}\sin k{\rm\pi}\mathop{\sum }_{n=2}^{\infty }(-1)^{n}{\it\eta}(k,n){\it\eta}(k,n+1)\left[4k{\it\delta}(n+1)(2n^{2}+3n+2)\sin {\it\chi}\right.\nonumber\\ \displaystyle & & \displaystyle +\,k^{2}(2n^{2}-2n-1)[({\it\delta}^{2}-1)\cos 2{\it\psi}-{\it\delta}^{2}+2{\it\delta}\cos {\it\chi}\sin 2{\it\psi}-1]\nonumber\\ \displaystyle & & \displaystyle +\,\left.2n(n+2)(n+1)^{2}[({\it\delta}^{2}-1)\cos 2{\it\psi}+{\it\delta}^{2}+2{\it\delta}\cos {\it\chi}\sin 2{\it\psi}+1]\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \bar{U}^{(2)} & = & \displaystyle -6a{\it\sigma}{\it\eta}(k,1){\it\eta}(k,2)\sin k{\rm\pi}\nonumber\\ \displaystyle & & \displaystyle \times \,\left[\frac{3{\it\delta}\sin {\it\chi}}{k}+2({\it\delta}^{2}+2{\it\delta}\cos {\it\chi}\sin 2{\it\psi}+1)+2({\it\delta}^{2}-1)\cos 2{\it\psi}\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2}a{\it\sigma}\sin k{\rm\pi}\mathop{\sum }_{n=2}^{\infty }(-1)^{n}{\it\eta}(k,n){\it\eta}(k,n+1)\left[4k{\it\delta}(n+1)(2n^{2}+3n+2)\sin {\it\chi}\right.\nonumber\\ \displaystyle & & \displaystyle +\,k^{2}(2n^{2}-2n-1)[({\it\delta}^{2}-1)\cos 2{\it\psi}-{\it\delta}^{2}+2{\it\delta}\cos {\it\chi}\sin 2{\it\psi}-1]\nonumber\\ \displaystyle & & \displaystyle +\,\left.2n(n+2)(n+1)^{2}[({\it\delta}^{2}-1)\cos 2{\it\psi}+{\it\delta}^{2}+2{\it\delta}\cos {\it\chi}\sin 2{\it\psi}+1]\right].\end{eqnarray}$$
Note that (D 5) and (D 6) reduce to (3.8) and (3.9) respectively when
![]() ${\it\psi}=0$
.
${\it\psi}=0$
.