Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Li, Gaojin
Ostace, Anca
and
Ardekani, Arezoo M.
2016.
Hydrodynamic interaction of swimming organisms in an inertial regime.
Physical Review E,
Vol. 94,
Issue. 5,
Felderhof, B U
and
Jones, R B
2017.
Swimming of a sphere in a viscous incompressible fluid with inertia.
Fluid Dynamics Research,
Vol. 49,
Issue. 4,
p.
045510.
Nganguia, Herve
Pietrzyk, Kyle
and
Pak, On Shun
2017.
Swimming efficiency in a shear-thinning fluid.
Physical Review E,
Vol. 96,
Issue. 6,
Spelman, Tamsin A.
and
Lauga, Eric
2017.
Arbitrary axisymmetric steady streaming: flow, force and propulsion.
Journal of Engineering Mathematics,
Vol. 105,
Issue. 1,
p.
31.
Shaik, Vaseem A.
and
Ardekani, Arezoo M.
2017.
Motion of a model swimmer near a weakly deforming interface.
Journal of Fluid Mechanics,
Vol. 824,
Issue. ,
p.
42.
Djellouli, Adel
Marmottant, Philippe
Djeridi, Henda
Quilliet, Catherine
and
Coupier, Gwennou
2017.
Buckling Instability Causes Inertial Thrust for Spherical Swimmers at All Scales.
Physical Review Letters,
Vol. 119,
Issue. 22,
Walker, Benjamin J.
Ishimoto, Kenta
Wheeler, Richard J.
and
Gaffney, Eamonn A.
2018.
Response of monoflagellate pullers to a shearing flow: A simulation study of microswimmer guidance.
Physical Review E,
Vol. 98,
Issue. 6,
Mahalinkam, Raksha
Gong, Felicity
and
Khair, Aditya S.
2018.
Reduced-order model for inertial locomotion of a slender swimmer.
Physical Review E,
Vol. 97,
Issue. 4,
Martínez-Pedrero, F.
and
Tierno, P.
2018.
Advances in colloidal manipulation and transport via hydrodynamic interactions.
Journal of Colloid and Interface Science,
Vol. 519,
Issue. ,
p.
296.
Zöttl, Andreas
and
Stark, Holger
2018.
Simulating squirmers with multiparticle collision dynamics.
The European Physical Journal E,
Vol. 41,
Issue. 5,
Nganguia, Herve
and
Pak, On Shun
2018.
Squirming motion in a Brinkman medium.
Journal of Fluid Mechanics,
Vol. 855,
Issue. ,
p.
554.
Aragones, Juan L.
Yazdi, Shahrzad
and
Alexander-Katz, Alfredo
2018.
Diffusion of self-propelled particles in complex media.
Physical Review Fluids,
Vol. 3,
Issue. 8,
Ouyang, Zhenyu
Lin, Jianzhong
and
Ku, Xiaoke
2018.
Hydrodynamic properties of squirmer swimming in power-law fluid near a wall.
Rheologica Acta,
Vol. 57,
Issue. 10,
p.
655.
Ouyang, Zhenyu
Lin, Jianzhong
and
Ku, Xiaoke
2018.
The hydrodynamic behavior of a squirmer swimming in power-law fluid.
Physics of Fluids,
Vol. 30,
Issue. 8,
Mandujano, F.
and
Málaga, C.
2018.
On the forced flow around a rigid flapping foil.
Physics of Fluids,
Vol. 30,
Issue. 6,
Ouyang, Zhenyu
Lin, Jianzhong
and
Ku, Xiaoke
2019.
Hydrodynamic interaction between a pair of swimmers in power-law fluid.
International Journal of Non-Linear Mechanics,
Vol. 108,
Issue. ,
p.
72.
Lin, Zhaowu
and
Gao, Tong
2019.
Direct-forcing fictitious domain method for simulating non-Brownian active particles.
Physical Review E,
Vol. 100,
Issue. 1,
Walker, Benjamin J.
Wheeler, Richard J.
Ishimoto, Kenta
and
Gaffney, Eamonn A.
2019.
Boundary behaviours of Leishmania mexicana: A hydrodynamic simulation study.
Journal of Theoretical Biology,
Vol. 462,
Issue. ,
p.
311.
Ahana, P
and
Thampi, Sumesh P
2019.
Confinement induced trajectory of a squirmer in a two dimensional channel.
Fluid Dynamics Research,
Vol. 51,
Issue. 6,
p.
065504.
Felderhof, B.U.
and
Jones, R.B.
2019.
Second harmonic generation and vortex shedding by a dipole-quadrupole and a quadrupole–octupole swimmer in a viscous incompressible fluid.
European Journal of Mechanics - B/Fluids,
Vol. 77,
Issue. ,
p.
299.
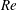 $Re$) between 0.01 and 1000 by numerical solution of the Navier–Stokes equations. A squirmer with a fixed swimming stroke and fixed swimming direction is considered. We find that fluid inertia leads to profound differences in the locomotion of pusher (propelled from the rear) versus puller (propelled from the front) squirmers. Specifically, pushers have a swimming speed that increases monotonically with
$Re$) between 0.01 and 1000 by numerical solution of the Navier–Stokes equations. A squirmer with a fixed swimming stroke and fixed swimming direction is considered. We find that fluid inertia leads to profound differences in the locomotion of pusher (propelled from the rear) versus puller (propelled from the front) squirmers. Specifically, pushers have a swimming speed that increases monotonically with 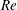 $Re$, and efficient convection of vorticity past their surface leads to steady axisymmetric flow that remains stable up to at least
$Re$, and efficient convection of vorticity past their surface leads to steady axisymmetric flow that remains stable up to at least 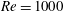 $Re=1000$. In contrast, pullers have a swimming speed that is non-monotonic with
$Re=1000$. In contrast, pullers have a swimming speed that is non-monotonic with 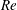 $Re$. Moreover, they trap vorticity within their wake, which leads to flow instabilities that cause a decrease in the time-averaged swimming speed at large
$Re$. Moreover, they trap vorticity within their wake, which leads to flow instabilities that cause a decrease in the time-averaged swimming speed at large 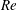 $Re$. The power expenditure and swimming efficiency are also computed. We show that pushers are more efficient at large
$Re$. The power expenditure and swimming efficiency are also computed. We show that pushers are more efficient at large 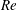 $Re$, mainly because the flow around them can remain stable to much greater
$Re$, mainly because the flow around them can remain stable to much greater 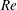 $Re$ than is the case for pullers. Interestingly, if unstable axisymmetric flows at large
$Re$ than is the case for pullers. Interestingly, if unstable axisymmetric flows at large 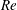 $Re$ are considered, pullers are more efficient due to the development of a Hill’s vortex-like wake structure.
$Re$ are considered, pullers are more efficient due to the development of a Hill’s vortex-like wake structure.


