Article contents
Spiralling liquid jets: verifiable mathematical framework, trajectories and peristaltic waves
Published online by Cambridge University Press: 24 April 2017
Abstract
The dynamics of a jet of an inviscid incompressible liquid spiralling out under the action of centrifugal forces is considered with both gravity and the surface tension taken into account. This problem is of direct relevance to a number of industrial applications, ranging from the spinning disc atomization process to nanofibre formation. The mathematical description of the flow by necessity requires the use of a local curvilinear non-orthogonal coordinate system centred around the jet’s baseline, and we present the general formulation of the problem without assuming that the jet is slender. To circumvent the inconvenience inherent in the non-orthogonality of the local coordinate system, the orthonormal Frenet basis is used in parallel with the local non-orthogonal basis, and the equation of motion, with the velocity considered with respect to the local coordinate system, is projected onto the Frenet basis. The variation of the latter along the baseline is then described by the Frenet equations which naturally brings the baseline’s curvature and torsion into the equations of motion. This technique allows one to handle different line-based non-orthogonal curvilinear coordinate systems in a straightforward and mathematically transparent way. An analysis of the slender-jet approximation that follows the general formulation shows how a set of ordinary differential equations describing the jet’s trajectory can be derived in two cases: 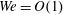 $\mathit{We}=O(1)$ and
$\mathit{We}=O(1)$ and 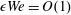 $\unicode[STIX]{x1D716}\mathit{We}=O(1)$ as
$\unicode[STIX]{x1D716}\mathit{We}=O(1)$ as 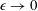 $\unicode[STIX]{x1D716}\rightarrow 0$, where
$\unicode[STIX]{x1D716}\rightarrow 0$, where  $\unicode[STIX]{x1D716}$ is the ratio of characteristic length scales across and along the jet and
$\unicode[STIX]{x1D716}$ is the ratio of characteristic length scales across and along the jet and 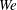 $\mathit{We}$ is the Weber number. A one-dimensional model for the propagation of nonlinear peristaltic disturbances along the jet is derived in each of these cases. A critical review of the work published on this topic is presented showing where errors typically occur and how to identify and avoid them.
$\mathit{We}$ is the Weber number. A one-dimensional model for the propagation of nonlinear peristaltic disturbances along the jet is derived in each of these cases. A critical review of the work published on this topic is presented showing where errors typically occur and how to identify and avoid them.
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 18
- Cited by



