Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T19:33:40.844Z Has data issue: false hasContentIssue false
  • English
  • Français

Spin-down of a barotropic vortex by irregular small-scale topography

Published online by Cambridge University Press:  22 June 2022

Timour Radko Open the ORCID record for Timour Radko [Opens in a new window]
Timour Radko*
Affiliation:
Department of Oceanography, Naval Postgraduate School, Monterey, CA 93943, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

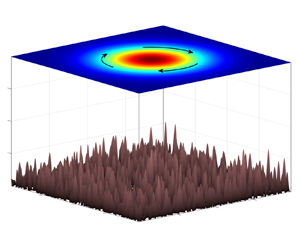
This study examines the impact of small-scale irregular topographic features on the dynamics and evolution of large-scale barotropic flows in the ocean. A multiscale theory is developed, which makes it possible to represent large-scale effects of the bottom roughness without explicitly resolving small-scale variability. The analytical model reveals that the key mechanism of topographic control involves the generation of a small-scale eddy field associated with considerable Reynolds stresses. These eddy stresses are inversely proportional to the large-scale velocity and adversely affect mean circulation patterns. The multiscale model is applied to the problem of topography-induced spin-down of a large circularly symmetric vortex and is validated by corresponding topography-resolving simulations. The small-scale bathymetry chosen for this configuration conforms to the Goff–Jordan statistical spectrum. While the multiscale model formally assumes a substantial separation between the scales of interacting flow components, it is remarkably accurate even when scale separation is virtually non-existent.

JFM classification

Geophysical and Geological Flows: Ocean circulation Geophysical and Geological Flows: Topographic effects
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 944 , 10 August 2022 , A5
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arbic, B., Fringer, O., Klymak, J., Mayer, F., Trossman, D. & Zhu, P. 2019 Connecting process models of topographic wave drag to global eddying general circulation models. Oceanography 32, 146–155.CrossRefGoogle Scholar
Balmforth, N.J. & Young, Y.-N. 2002 Stratified Kolmogorov flow. J. Fluid Mech. 450, 131–167.CrossRefGoogle Scholar
Balmforth, N.J. & Young, Y.-N. 2005 Stratified Kolmogorov flow. Part 2. J. Fluid Mech. 528, 23–42.CrossRefGoogle Scholar
Benilov, E.S. 2000 The stability of zonal jets in a rough-bottomed ocean on the barotropic beta plane. J. Phys. Oceanogr. 30, 733–740.2.0.CO;2>CrossRefGoogle Scholar
Benilov, E.S. 2001 Baroclinic instability of two-layer flows over one-dimensional bottom topography. J. Phys. Oceanogr. 31, 2019–2025.2.0.CO;2>CrossRefGoogle Scholar
Bobrovich, A.V. & Reznik, G.M. 1999 Planetary waves in a stratified ocean of variable depth. Part 2. Continuously stratified ocean. J. Fluid Mech. 388, 147–169.CrossRefGoogle Scholar
Brown, J., Gulliver, L. & Radko, T. 2019 Effects of topography and orientation on the nonlinear equilibration of baroclinic instability. J. Geophys. Res. Oceans 124, 6720–6734.CrossRefGoogle Scholar
Chen, C., Kamenkovich, I. & Berloff, P. 2015 On the dynamics of flows induced by topographic ridges. J. Phys. Oceanogr. 45, 927–940.CrossRefGoogle Scholar
Dewar, W.K. 1986 On the potential vorticity structure of weakly ventilated isopycnals: a theory of subtropical mode water maintenance. J. Phys. Oceanogr. 16, 1204–1216.2.0.CO;2>CrossRefGoogle Scholar
Dewar, W.K. 1998 Topography and barotropic transport control by bottom friction. J. Mar. Res. 56, 295–328.CrossRefGoogle Scholar
Early, J.J., Samelson, R.M. & Chelton, D.B. 2011 The evolution and propagation of quasigeostrophic ocean eddies. J. Phys. Oceanogr. 41, 1535–1555.CrossRefGoogle Scholar
Eden, C., Olbers, D. & Eriksen, T. 2021 A closure for lee wave drag on the large-scale ocean circulation. J. Phys. Oceanogr. 51, 3573–3588.Google Scholar
Gama, S., Vergassola, M. & Frisch, U. 1994 Negative eddy viscosity in isotropically forced 2-dimensional flow – linear and nonlinear dynamics. J. Fluid Mech. 260, 95–126.CrossRefGoogle Scholar
Goff, J.A. 2020 Identifying characteristic and anomalous mantle from the complex relationship between abyssal hill roughness and spreading rates. Geophys. Res. Lett. 47, e2020GL088162.CrossRefGoogle Scholar
Goff, J.A. & Jordan, T.H. 1988 Stochastic modeling of seafloor morphology: inversion of sea beam data for second-order statistics. J. Geophys. Res. 93, 13589–13608.CrossRefGoogle Scholar
Goldsmith, E.J. & Esler, J.G. 2021 Wave propagation in rotating shallow water in the presence of small-scale topography. J. Fluid Mech. 923, A24.CrossRefGoogle Scholar
Gulliver, L. & Radko, T. 2022 Topographic stabilization of ocean rings. Geophys. Res. Lett. 49, e2021GL097686.CrossRefGoogle Scholar
Holloway, G. 1987 Systematic forcing of large-scale geophysical flows by eddy-topography interaction. J. Fluid Mech. 184, 463–476.CrossRefGoogle Scholar
Holloway, G. 1992 Representing topographic stress for large-scale ocean models. J. Phys. Oceanogr. 22, 1033–1046.2.0.CO;2>CrossRefGoogle Scholar
Hughes, C.W. & De Cuevas, B.A. 2001 Why western boundary currents in realistic oceans are inviscid: a link between form stress and bottom pressure torques. J. Phys. Oceanogr. 31, 2871–2885.2.0.CO;2>CrossRefGoogle Scholar
Johnson, E.R. 1978 Trapped vortices in rotating flow. J. Fluid Mech. 86, 209–224.CrossRefGoogle Scholar
Klymak, J.M., Balwada, D., Garabato, A.N. & Abernathey, R. 2021 Parameterizing nonpropagating form drag over rough bathymetry. J. Phys. Oceanogr. 51, 1489–1501.CrossRefGoogle Scholar
LaCasce, J., Escartin, J., Chassignet, E.P. & Xu, X. 2019 Jet instability over smooth, corrugated, and realistic bathymetry. J. Phys. Oceanogr. 49, 585–605.CrossRefGoogle Scholar
Manfroi, A. & Young, W. 1999 Slow evolution of zonal jets on the beta plane. J. Atmos. Sci. 56, 784–800.2.0.CO;2>CrossRefGoogle Scholar
Manfroi, A. & Young, W. 2002 Stability of beta-plane Kolmogorov flow. Physica D 162, 208–232.CrossRefGoogle Scholar
Marshall, D. 1995 Topographic steering of the Antarctic Circumpolar Current. J. Phys. Oceanogr. 25, 1636–1650.2.0.CO;2>CrossRefGoogle Scholar
Marshall, D.P., Williams, R.G. & Lee, M.M. 1999 The relation between eddy-induced transport and isopycnic gradients of potential vorticity. J. Phys. Oceanogr. 29, 1571–1578.2.0.CO;2>CrossRefGoogle Scholar
Mei, C.C. & Vernescu, M. 2010 Homogenization Methods for Multiscale Mechanics. World Scientific.CrossRefGoogle Scholar
Merryfield, W.J. & Holloway, G. 1997 Topographic stress parameterization in a quasi-geostrophic barotropic model. J. Fluid Mech. 341, 1–18.CrossRefGoogle Scholar
Merryfield, W.J. & Holloway, G. 1999 Eddy fluxes and topography in stratified quasi-geostrophic models. J. Fluid Mech. 380, 59–80.CrossRefGoogle Scholar
Munk, W.H. 1950 On the wind-driven ocean circulation. J. Atmos. Sci. 7, 80–93.Google Scholar
Nikurashin, M., Ferrari, R., Grisouard, N. & Polzin, K. 2014 The impact of finite-amplitude bottom topography on internal wave generation in the Southern Ocean. J. Phys. Oceanogr. 44, 2938–2950.CrossRefGoogle Scholar
Novikov, A. & Papanicolau, G. 2001 Eddy viscosity of cellular flows. J. Fluid Mech. 446, 173–198.CrossRefGoogle Scholar
Olbers, D., Borowski, D., Völker, C. & Wolff, J.-O. 2004 The dynamical balance, transport and circulation of the Antarctic Circumpolar Current. Antarct. Sci. 16, 439–470.CrossRefGoogle Scholar
Pedlosky, J. 1987 Geophysical Fluid Dynamics. Springer.CrossRefGoogle Scholar
Radko, T. 2011 a On the generation of large-scale structures in a homogeneous eddy field. J. Fluid Mech. 668, 76–99.CrossRefGoogle Scholar
Radko, T. 2011 b Eddy viscosity and diffusivity in the modon-sea model. J. Mar. Res. 69, 723–752.CrossRefGoogle Scholar
Radko, T. 2016 On the spontaneous generation of large-scale eddy-induced patterns: the average eddy model. J. Fluid. Mech. 809, 316–344.CrossRefGoogle Scholar
Radko, T. 2020 Control of baroclinic instability by submesoscale topography. J. Fluid Mech. 882, A14.CrossRefGoogle Scholar
Radko, T. 2021 Barotropic instability of a time-dependent parallel flow. J. Fluid Mech. 922, A11.CrossRefGoogle Scholar
Radko, T. & Kamenkovich, I. 2017 On the topographic modulation of large-scale eddying flows. J. Phys. Oceanogr. 47, 2157–2172.CrossRefGoogle Scholar
Reznik, G.M. & Tsybaneva, T.B. 1999 Planetary waves in a stratified ocean of variable depth. Part 1. Two-layer model. J. Fluid Mech. 388, 115–145.CrossRefGoogle Scholar
Rhines, P.B. & Young, W.R. 1982 Homogenization of potential vorticity in planetary gyres. J. Fluid Mech. 122, 347–367.CrossRefGoogle Scholar
Sansón, L.Z., & van Heijst, G.J.F. 2014 Laboratory experiments on flows over bottom topography. In Modeling Atmospheric and Oceanic Flows: Insights from Laboratory Experiments and Numerical Simulations (ed. von Larcher, T. & Williams, P.D.), pp. 139–158. Wiley.Google Scholar
Stommel, H. 1948 The westward intensification of wind-driven ocean currents. Eos Trans. AGU 29, 202–206.CrossRefGoogle Scholar
Sutyrin, G.G. & Radko, T. 2019 On the peripheral intensification of two-dimensional vortices in a small-scale randomly forced flow. Phys. Fluids 31, 101701.CrossRefGoogle Scholar
Taylor, G.I. 1923 Experiments on the motion of solid bodies in rotating fluids. Proc. Roy. Soc. A 104, 213–218.Google Scholar
Trossman, D.S., Arbic, B.K., Straub, D.N., Richman, J.G., Chassignet, E.P., Wallcraftand, A.J. & Xu, X. 2017 The role of rough topography in mediating impacts of bottom drag in eddying ocean circulation models. J. Phys. Oceanogr. 47, 1941–1959.CrossRefGoogle ScholarPubMed
Vanneste, J. 2000 Enhanced dissipation for quasi-geostrophic motion over small-scale topography. J. Fluid Mech. 407, 105–122.CrossRefGoogle Scholar
Vanneste, J. 2003 Nonlinear dynamics over rough topography: homogeneous and stratified quasi-geostrophic theory. J. Fluid Mech. 474, 299–318.CrossRefGoogle Scholar
Wåhlin, A.K. 2002 Topographic steering of dense currents with application to submarine canyons. Deep-Sea Res. I: Oceanogr. Res. Papers 49, 305–320.CrossRefGoogle Scholar