Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-02T20:12:12.608Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectral analysis of the budget equation in turbulent channel flows at high Reynolds number

Published online by Cambridge University Press:  14 December 2018

Myoungkyu Lee Open the ORCID record for Myoungkyu Lee [Opens in a new window]  and
Robert D. Moser Open the ORCID record for Robert D. Moser [Opens in a new window]
Myoungkyu Lee
Affiliation:
Center for Predictive Engineering and Computational Sciences, Insititute for Computational Engineering and Sciences, The University of Texas at Austin, TX 78712, USA
Robert D. Moser*
Affiliation:
Center for Predictive Engineering and Computational Sciences, Insititute for Computational Engineering and Sciences, The University of Texas at Austin, TX 78712, USA Department of Mechanical Engineering, The University of Texas at Austin, TX 78712, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The transport equations for the variances of the velocity components are investigated using data from direct numerical simulations of incompressible channel flows at friction Reynolds number ($Re_{\unicode[STIX]{x1D70F}}$) up to 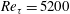$Re_{\unicode[STIX]{x1D70F}}=5200$. Each term in the transport equation has been spectrally decomposed to expose the contribution of turbulence at different length scales to the processes governing the flow of energy in the wall-normal direction, in scale and among components. The outer-layer turbulence is dominated by very large-scale streamwise elongated modes, which are consistent with the very large-scale motions (VLSM) that have been observed by many others. The presence of these VLSMs drives many of the characteristics of the turbulent energy flows. Away from the wall, production occurs primarily in these large-scale streamwise-elongated modes in the streamwise velocity, but dissipation occurs nearly isotropically in both velocity components and scale. For this to happen, the energy is transferred from the streamwise-elongated modes to modes with a range of orientations through nonlinear interactions, and then transferred to other velocity components. This allows energy to be transferred more-or-less isotropically from these large scales to the small scales at which dissipation occurs. The VLSMs also transfer energy to the wall region, resulting in a modulation of the autonomous near-wall dynamics and the observed Reynolds number dependence of the near-wall velocity variances. The near-wall energy flows are more complex, but are consistent with the well-known autonomous near-wall dynamics that gives rise to streaks and streamwise vortices. Through the overlap region between outer- and inner-layer turbulence, there is a self-similar structure to the energy flows. The VLSM production occurs at spanwise scales that grow with 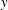$y$. There is transport of energy away from the wall over a range of scales that grows with 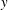$y$. Moreover, there is transfer of energy to small dissipative scales which grows like 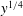$y^{1/4}$, as expected from Kolmogorov scaling. Finally, the small-scale near-wall processes characterised by wavelengths less than 1000 wall units are largely Reynolds number independent, while the larger-scale outer-layer processes are strongly Reynolds number dependent. The interaction between them appears to be relatively simple.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 860 , 10 February 2019 , pp. 886 - 938
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Combustion Research Facility, Sandia National Laboratories, Livermore, CA 94550, USA.

References

Afzal, N. 1982 Fully developed turbulent flow in a pipe: an intermediate layer. Ingenieur-Archiv 52, 355–377.Google Scholar
Ahn, J., Lee, J. & Sung, H. J. 2017 Contribution of large-scale motions to the Reynolds shear stress in turbulent pipe flows. Intl J. Heat Fluid Flow 66, 209–216.Google Scholar
Ahn, J., Lee, J. H., Lee, J., Kang, J.-h. & Sung, H. J. 2015 Direct numerical simulation of a 30R long turbulent pipe flow at Re 𝜏 = 3008. Phys. Fluids 27, 065110.Google Scholar
Ahn, J. & Sung, H. J. 2017 Relationship between streamwise and azimuthal length scales in a turbulent pipe flow. Phys. Fluids 29 (10), 105112.Google Scholar
del Álamo, J. C. & Jiménez, J. 2003 Spectra of the very large anisotropic scales in turbulent channels. Phys. Fluids 15 (6), L41–L44.Google Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.Google Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2006 Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 561, 329–358.Google Scholar
Antonia, R. A., Djenidi, L. & Spalart, P. R. 1994 Anisotropy of the dissipation tensor in a turbulent boundary layer. Phys. Fluids 6 (7), 2475–2479.Google Scholar
Antonia, R. A., Kim, J. & Browne, L. W. B. 1991 Some characteristics of small-scale turbulence in a turbulent duct flow. J. Fluid Mech. 233, 369–388.Google Scholar
Aulery, F., Dupuy, D., Toutant, A., Bataille, F. & Zhou, Y. 2017 Spectral analysis of turbulence in anisothermal channel flows. Comput. Fluids 151, 115–131.Google Scholar
Baltzer, J. R., Adrian, R. J. & Wu, X. 2013 Structural organization of large and very large scales in turbulent pipe flow simulation. J. Fluid Mech. 720, 236–279.Google Scholar
Bolotnov, I. A., Lahey, R. T. Jr, Drew, D. A., Jansen, K. E. & Oberai, A. A. 2010 Spectral analysis of turbulence based on the DNS of a channel flow. Comput. Fluids 39 (4), 640–655.Google Scholar
Chandran, D., Baidya, R., Monty, J. P. & Marusic, I. 2017 Two-dimensional energy spectra in high-Reynolds-number turbulent boundary layers. J. Fluid Mech. 826, R1.Google Scholar
Chin, C., Philip, J., Klewicki, J., Ooi, A. & Marusic, I. 2014 Reynolds-number-dependent turbulent inertia and onset of log region in pipe flows. J. Fluid Mech. 757, 747–769.Google Scholar
Cimarelli, A., De Angelis, E. & Casciola, C. M. 2013 Paths of energy in turbulent channel flows. J. Fluid Mech. 715, 436–451.Google Scholar
Cimarelli, A., De Angelis, E., Jiménez, J. & Casciola, C. M. 2016 Cascades and wall-normal fluxes in turbulent channel flows. J. Fluid Mech. 796, 417–436.Google Scholar
Cimarelli, A., De Angelis, E., Schlatter, P., Brethouwer, G., Talamelli, A. & Casciola, C. M. 2015 Sources and fluxes of scale energy in the overlap layer of wall turbulence. J. Fluid Mech. 771, 407–423.Google Scholar
DeGraaff, D. B. & Eaton, J. K. 2000 Reynolds-number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.Google Scholar
Domaradzki, J. A., Liu, W., Härtel, C. & Kleiser, L. 1994 Energy transfer in numerically simulated wall-bounded turbulent flows. Phys. Fluids 6 (4), 1583–1599.Google Scholar
Fernholz, H. H. & Finley, P. J. 1996 The incompressible zero-pressure-gradient turbulent boundary layer: an assessment of the data. Prog. Aerosp. Sci. 32, 245–311.Google Scholar
Ganapathisubramani, B., Hutchins, N., Monty, J. P., Chung, D. & Marusic, I. 2012 Amplitude and frequency modulation in wall turbulence. J. Fluid Mech. 712, 61–91.Google Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.Google Scholar
Hamilton, J. M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.Google Scholar
Hoyas, S. & Jiménez, J. 2008 Reynolds number effects on the Reynolds-stress budgets in turbulent channels. Phys. Fluids 20, 101511.Google Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2012 Turbulent pipe flow at extreme Reynolds numbers. Phys. Rev. Lett. 108, 094501.Google Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2013 Logarithmic scaling of turbulence in smooth- and rough-wall pipe flow. J. Fluid Mech. 728, 376–395.Google Scholar
Hutchins, N. & Marusic, I. 2007a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Hutchins, N. & Marusic, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365, 647–664.Google Scholar
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.Google Scholar
Hwang, Y. 2015 Statistical structure of self-sustaining attached eddies in turbulent channel flow. J. Fluid Mech. 767, 254–289.Google Scholar
Jeong, J., Hussain, F., Schoppa, W. & Kim, J. 1997 Coherent structures near the wall in a turbulent channel flow. J. Fluid Mech. 332, 185–214.Google Scholar
Jiménez, J. 2012 Cascades in wall-bounded turbulence. Annu. Rev. Fluid Mech. 44, 27–45.Google Scholar
Jiménez, J. 2018 Coherent structures in wall-bounded turbulence. J. Fluid Mech. 842, P1.Google Scholar
Jiménez, J. & Hoyas, S. 2008 Turbulent fluctuations above the buffer layer of wall-bounded flows. J. Fluid Mech. 611, 215–236.Google Scholar
Jiménez, J. & Moser, R. D. 2007 What are we learning from simulating wall turbulence? Phil. Trans. R. Soc. Lond. A 365, 715–732.Google Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Kraheberger, S., Hoyas, S. & Oberlack, M. 2018 DNS of a turbulent Couette flow at constant wall transpiration up to Re 𝜏 = 1000. J. Fluid Mech. 835, 421–443.Google Scholar
Kunkel, G. J. & Marusic, I. 2006 Study of the near-wall-turbulent region of the high-Reynolds-number boundary layer using an atmospheric flow. J. Fluid Mech. 548, 375–402.Google Scholar
Lee, M., Malaya, N. & Moser, R. D. 2013 Petascale direct numerical simulation of turbulent channel flow on up to 786K cores. In The International Conference for High Performance Computing, Networking, Storage and Analysis, pp. 1–11. ACM Press.Google Scholar
Lee, M. & Moser, R. D. 2015a Direct numerical simulation of turbulent channel flow up to Re 𝜏 = 5200. J. Fluid Mech. 774, 395–415.Google Scholar
Lee, M. & Moser, R. D. 2015b Spectral analysis on Reynolds stress transport equation in high Re wall-bounded turbulence. In Ninth International Symposium on Turbulence and Shear Flow Phenomena, art. 4A-3.Google Scholar
Lee, M., Ulerich, R., Malaya, N. & Moser, R. D. 2014 Experiences from leadership computing in simulations of turbulent fluid flows. Comput. Sci. Engng 16 (5), 24–31.Google Scholar
Lee, M. J., Kim, J. & Moin, P. 1990 Structure of turbulence at high shear rate. J. Fluid Mech. 216, 561–583.Google Scholar
Luchini, P. 2018 Structure and interpolation of the turbulent velocity profile in parallel flow. Eur. J. Mech. (B/Fluids) 71, 15–34.Google Scholar
Lumley, J. L. 1964 Spectral energy budget in wall turbulence. Phys. Fluids 7 (2), 190–196.Google Scholar
Lumley, J. L. 1975 Pressure–strain correlation. Phys. Fluids 18 (6), 750.Google Scholar
Lumley, J. L. 1979 Computational modeling of turbulent flows. In Advances in Applied Mechanics, pp. 123–176. Elsevier.Google Scholar
Mansour, N. N., Kim, J. & Moin, P. 1988 Reynolds-stress and dissipation-rate budgets in a turbulent channel flow. J. Fluid Mech. 194, 15–44.Google Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010a High Reynolds number effects in wall turbulence. Intl J. Heat Fluid Flow 31 (3), 418–428.Google Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010b Predictive model for wall-bounded turbulent flow. Science 329, 193–196.Google Scholar
Marusic, I., McKeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010c Wall-bounded turbulent flows at high Reynolds numbers: recent advances and key issues. Phys. Fluids 22, 065103.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Millikan, C. B. 1938 A critical discussion of turbulent flows in channels and circular tubes. In Proceedings of the Fifth International Congress for Applied Mechanics, pp. 386–392.Google Scholar
Mizuno, Y. 2015 Spectra of turbulent energy transport in channel flows. In 15th European Turbulence Conference.Google Scholar
Mizuno, Y. 2016 Spectra of energy transport in turbulent channel flows for moderate Reynolds numbers. J. Fluid Mech. 805, 171–187.Google Scholar
Mizuno, Y. & Jiménez, J. 2011 Mean velocity and length-scales in the overlap region of wall-bounded turbulent flows. Phys. Fluids 23, 085112.Google Scholar
Monkewitz, P. A. 2017 Revisiting the quest for a universal log-law and the role of pressure gradient in ‘canonical’ wall-bounded turbulent flows. Phys. Rev. Fluids 2 (9), 094602.Google Scholar
Monty, J. P., Hutchins, N., Ng, H. C. H., Marusic, I. & Chong, M. S. 2009 A comparison of turbulent pipe, channel and boundary layer flows. J. Fluid Mech. 632, 431–442.Google Scholar
Morrison, J. F., McKeon, B. J., Jiang, W. & Smits, A. J. 2004 Scaling of the streamwise velocity component in turbulent pipe flow. J. Fluid Mech. 508, 99–131.Google Scholar
Nagib, H. M. & Chauhan, K. A. 2008 Variations of von Kármán coefficient in canonical flows. Phys. Fluids 20, 101518.Google Scholar
Perot, B. & Moin, P. 1995 Shear-free turbulent boundary layers. Part 1. Physical insights into near-wall turbulence. J. Fluid Mech. 295, 199–227.Google Scholar
Perry, A. E., Henbest, S. & Chong, M. S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.Google Scholar
Perry, A. E. & Marusic, I. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 1. Extension of the attached eddy hypothesis. J. Fluid Mech. 298, 361–388.Google Scholar
Richter, D. H. 2015 Turbulence modification by inertial particles and its influence on the spectral energy budget in planar Couette flow. Phys. Fluids 27 (6), 063304.Google Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.Google Scholar
de Silva, C. M., Marusic, I., Woodcock, J. D. & Meneveau, C. 2015 Scaling of second- and higher-order structure functions in turbulent boundary layers. J. Fluid Mech. 769, 654–686.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. The MIT Press.Google Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Vallikivi, M., Ganapathisubramani, B. & Smits, A. J. 2015 Spectral scaling in boundary layers and pipes at very high Reynolds numbers. J. Fluid Mech. 771, 303–326.Google Scholar
Woodcock, J. D. & Marusic, I. 2015 The statistical behaviour of attached eddies. Phys. Fluids 27, 015104.Google Scholar
Wu, X., Baltzer, J. R. & Adrian, R. J. 2012 Direct numerical simulation of a 30r long turbulent pipe flow at r = 685: large- and very large-scale motions. J. Fluid Mech. 698, 235–281.Google Scholar