Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-21T14:46:30.061Z Has data issue: false hasContentIssue false
  • English
  • Français

Spatiotemporal instability of a variable-density Batchelor vortex

Published online by Cambridge University Press:  12 June 2012

Bastien Di Pierro  and
Malek Abid
Bastien Di Pierro
Affiliation:
IRPHE – UMR 6594, Technopôle de Château-Gombert, 49 rue Joliot Curie – B.P. 146, 13384 Marseille CEDEX 13, France
Malek Abid*
Affiliation:
IRPHE – UMR 6594, Technopôle de Château-Gombert, 49 rue Joliot Curie – B.P. 146, 13384 Marseille CEDEX 13, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Linear and nonlinear impulse responses are computed, using three-dimensional numerical simulations, for an incompressible and variable density (inhomogeneous) Batchelor vortex at a moderately high Reynolds number, . In the linear framework, the computed wavepacket is decomposed into azimuthal modes whose growth rates are determined along each spatiotemporal ray, in the laboratory frame. It is found that the Batchelor vortex undergoes a convective/absolute transition when the density ratio (inner/ambient), , is varied solely (there is no need for an external counter flow to trigger this transition like that needed in the constant density case). More precisely, it is shown that the transition occurs for heavy vortices when the density ratio reaches a critical value, 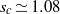. For light vortices (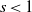) no transition was found. It is also shown that the first azimuthal mode that transits have an azimuthal wavenumber 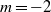and the transition occurs for a swirl number (a measure of the azimuthal to axial velocity ratio), 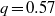. It is followed by 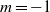, then by 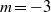. When nonlinearities are allowed, it is found that they saturate the amplitude within the linear-response wavepacket, leaving the wavepacket fronts unaffected. The conclusions should thus be the same as those obtained in the linear case: the linear convective/absolute transition should coincide with the nonlinear one for the variable-density Batchelor vortex.

JFM classification

Instability: Absolute/convective instability Instability: Nonlinear instability Vortex Flows: Vortex instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 703 , 25 July 2012 , pp. 49 - 59
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Abid, M. 2008 Nonlinear mode selection in a model of trailing line vortices. J. Fluid Mech. 605, 19–45.CrossRefGoogle Scholar
2. Abid, M. & Brachet, M. E. 1998 Direct numerical simulations of the batchelor trailing vortex by a spectral method. Phys. Fluids 10, 469–475.CrossRefGoogle Scholar
3. Batchelor, G. K. 1964 Axial flow in trailing line vortices. J. Fluid Mech. 20, 645–658.CrossRefGoogle Scholar
4. Chorin, A. J. 1968 Numerical solution of the Navier–Stokes equations. Maths Comput. 22 (104), 745–762.CrossRefGoogle Scholar
5. Coquart, L., Sipp, D. & Jacquin, L. 2005 Mixing induced by Rayleigh–Taylor instability in a vortex. Phys. Fluids 17 (2), 021703.CrossRefGoogle Scholar
6. Delbende, I. & Chomaz, J. M. 1998 Nonlinear convective/absolute instabilities in parallel two-dimensionnal wakes. Phys. Fluids 10, 2724–2736.CrossRefGoogle Scholar
7. Delbende, I., Chomaz, J. M. & Huerre, P. 1998 Absolute/convective instabilitites in the Batchelor vortex: a numerical study of the linear impulse response. J. Fluid Mech. 335, 229–254.CrossRefGoogle Scholar
8. Di Pierro, B. & Abid, M. 2010 Instabilities of variable-density swirling flows. Phys. Rev. E 82 (046312).CrossRefGoogle ScholarPubMed
9. Di Pierro, B. & Abid, M. 2011 Energy spectra in helical vortex breakdown. Phys. Fluids 22, 25104.CrossRefGoogle Scholar
10. Di Pierro, B. & Abid, M. 2012 Rayleigh–Taylor instability in variable density swirling flows. Euro. Phys. J. B - Condens. Matter Complex Syst. 85 (2), 69.CrossRefGoogle Scholar
11. Gallaire, F. & Chomaz, J. M. 2003 Mode selection in swirling jet experiments: a linear stability analysis. J. Fluid Mech. 494, 223–253.CrossRefGoogle Scholar
12. Gallaire, F., Ruith, M., Meiburg, E., Chomaz, J. M. & Huerre, P. 2006 Spiral vortex breakdown as a global mode. J. Fluid Mech. 549, 71–80.CrossRefGoogle Scholar
13. Huerre, P. & Monkewitz, P. A. 1985 Absolute and convective instabilities in free shear layers. J. Fluid Mech. 159, 151–168.CrossRefGoogle Scholar
14. Landau, L. D. & Lifshitz, E. M. 1987 Fluid Mechanics. Pergamon.Google Scholar
15. Lessen, M. & Paillet, F. 1974 The stability of a trailing line vortex. Part 2. Viscous theory. J. Fluid Mech. 65, 769–779.CrossRefGoogle Scholar
16. Lessen, M., Singh, P. W. & Paillet, F. 1974 The stability of a trailing line vortex. Part 1. Inviscid theory. J. Fluid Mech. 63, 753–763.CrossRefGoogle Scholar
17. Olendraru, C. & Sellier, A. 2002 Viscous effects in the absolute-convective instability of the Batchelor vortex. J. Fluid Mech. 459, 371–396.CrossRefGoogle Scholar
18. Olendraru, C., Sellier, A., Rossi, M. & Huerre, P. 1996 Absolute/convective instability of the Batchelor vortex. J. Fluid Mech. 323, 153–159.Google Scholar
19. Parras, L. & Fernandez-Feria, R. 2007 Spatial stability and the onset of absolute instability of Batchelor’s vortex for high swirl numbers. J. Fluid Mech. 583, 27–43.CrossRefGoogle Scholar
20. Ruith, M. R., Chen, P., Meiburg, E. & Maxworthy, T. 2003 Three-dimensional vortex breakdown in swirling jets and wakes: direct numerical simulation. J. Fluid Mech. 486, 331–378.CrossRefGoogle Scholar
21. Schwartz, M., Bennet, W. & Stein, S. 1966 Communication Systems and Techniques. McGraw-Hill.Google Scholar
22. Twiss, R. Q. 1952 Propagation in electron–ion streams. Phys. Rev. 88, 1392–1407.CrossRefGoogle Scholar