Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T16:18:10.200Z Has data issue: false hasContentIssue false
  • English
  • Français

Spatially and temporally resolved measurements of bead resuspension and saltation in a turbulent water channel flow

Published online by Cambridge University Press:  09 January 2013

René van Hout
René van Hout*
Affiliation:
Faculty of Mechanical Engineering, Technion–Israel Institute of Technology, Haifa 32000, Israel
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Resuspension and saltation of nearly neutrally buoyant polystyrene beads $({d}_{p} = 583\pm 14. 4~\lrm{\ensuremath{\mu}} \mathrm{m} , {\rho }_{p} = 1050~\mathrm{kg} ~{\mathrm{m} }^{\ensuremath{-} 3} )$ in a turbulent boundary layer were studied using time-resolved particle image velocimetry and particle tracking velocimetry in a horizontal water channel facility 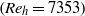$({\mathit{Re}}_{h} = 7353)$. The time difference between frames was 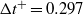$ \mrm{\Delta} {t}^{+ } = 0. 297$, comparable to the particle Stokes number, 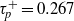${ \tau }_{p}^{+ } = 0. 267$. Near-wall coherent structures were visualized using spatial distributions of vorticity and swirling strength in combination with those of the instantaneous 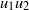${u}_{1} {u}_{2} $ correlations and 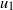${u}_{1} $. Two case studies, the first on resuspension and the second on saltation, showed that in all cases lift-off coincided with the passage of a vortex core, creating an ejection-sweep cycle (‘burst’) responsible for lift-off. In all cases beads left the wall when immersed in near-wall ejections and exposed to positive shear. As a consequence, a high shear-induced lift force coincided with bead lift-off, while the Magnus force due to bead rotation and translation-induced lift were negligible. The wall-normal component of the drag force mostly opposed lift-off, causing the bead’s deceleration. The difference between resuspension and saltation was governed by the type of coherent flow structures encountered by the beads when lifted out of the viscous sublayer. Resuspension was observed when beads were carried upwards by the combined action of a strong, spatially coherent upstream fast moving $({u}_{1} \gt 0)$ flow structure and a downstream ejection. On the other hand, saltation was accompanied by similar but weaker and spatially less coherent near-wall turbulence structures.

JFM classification

Multiphase and Particle-laden Flows: Particle/fluid flow Geophysical and Geological Flows: Sediment transport Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 715 , 25 January 2013 , pp. 389 - 423
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J., Christensen, K. T. & Liu, Z.-C. 2000 Analysis and interpretation of instantaneous turbulent velocity fields. Exp. Fluids 29, 275–290.Google Scholar
Ancey, C., Bigillon, F., Frey, P., Lanier, J. & Ducret, R. 2002 Saltating motion of a bead in a rapid water stream. Phys. Rev. E 66, 036306.CrossRefGoogle Scholar
Aylor, D. E., Schultes, N. P. & Shields, E. J. 2003 An aerobiological framework for assessing cross-pollination in maize. Agric. Forest Meteorol. 119, 111–129.Google Scholar
Bagnold, R. A. 1951 The movement of a cohesionless granular bed by fluid flow over it. Brit. J. Appl. Phys. 2, 29–34.Google Scholar
Borowsky, J. & Wei, T. 2006 Simultaneous velocimetry/accelerometry measurements in a turbulent two-phase pipe flow. Exp. Fluids 41, 13–20.Google Scholar
Braaten, D. A., Paw U, K. T. & Shaw, R. H. 1988 Coherent turbulent structures and particle detachment in boundary layer flows. J. Aerosol Sci. 19, 1183–1186.Google Scholar
Braaten, D. A., Paw U, K. T. & Shaw, R. H. 1990 Particle resuspension in a turbulent boundary layer: observed and modelled. J. Aerosol Sci. 21, 613–628.CrossRefGoogle Scholar
Cellino, M. & Lemmin, U. 2004 Influence of coherent flow structures on the dynamics of suspended sediment transport in open channel flow. J. Hydraul. Engng 1077–1088.Google Scholar
Cherukat, P. & McLaughlin, J. B. 1990 Wall-induced lift on a sphere. Intl J. Multiphase Flow 16, 899–907.Google Scholar
Cleaver, J. W. & Yates, B. 1973 Mechanism of detachment of colloidal particles from a flat substrate in a turbulent flow. J. Colloid Interface Sci. 44, 464–474.Google Scholar
Dwivedi, A., Melville, B. W., Shamseldin, A. Y. & Guha, T. K. 2010 Drag force on a sediment particle from point velocity measurements: a spectral approach. Water Resour. Res. 46, W10529.CrossRefGoogle Scholar
Dwivedi, A., Melville, B. W., Shamseldin, A. Y. & Guha, T. K. 2011a Flow structures and hydrodynamic force during sediment entrainment. Water Resour. Res. 47, W01509.Google Scholar
Dwivedi, A., Melville, B. W., Shamseldin, A. Y. & Guha, T. K. 2011b Analysis of hydrodynamic lift on a bed sediment particle. J. Geophys. Res. 116, F02015.Google Scholar
Eaton, J. K. & Fessler, J. R. 1994 Preferential concentration of particles by turbulence. Intl J. Multiphase Flow 20, 169–209.Google Scholar
Ferrante, A. & Elghobashi, S. 2004 On the physical mechanisms of drag reduction in a spatially developing turbulent boundary layer laden with microbubbles. J. Fluid Mech. 503, 345–355.Google Scholar
Francis, J. R. D. 1973 Experiments on the motion of solitary grains along the bed of a water stream. Proc. R. Soc. Lond. A 332, 443–471.Google Scholar
Hall, D. 1988 Measurements of the mean force on a particle near a boundary in turbulent flow. J. Fluid Mech. 187, 451–466.Google Scholar
Hall, D. 1989 The time dependence of particle resuspension. J. Aerosol Sci. 20, 907–910.Google Scholar
van Hout, R. 2011 Time-resolved PIV measurements of the interaction of polystyrene beads with near-wall-coherent structures in a turbulent channel flow. Intl J. Multiphase Flow 37, 346–357.Google Scholar
Hurther, D. & Lemmin, U. 2003 Turbulent particle flux and momentum flux statistics in suspension flow. Water Resour. Res. 39 (5), 1139.Google Scholar
Kaftori, D., Hetsroni, G. & Banerjee, S. 1995a Particle behaviour in the turbulent boundary layer. Part 1. Motion, deposition and entrainment. Phys. Fluids 7, 1095–1106.Google Scholar
Kaftori, D., Hetsroni, G. & Banerjee, S. 1995b Particle behaviour in the turbulent boundary layer. Part 2. Velocity and distribution profiles. Phys. Fluids 7, 1107–1121.Google Scholar
Kaftori, D., Hetsroni, G. & Banerjee, S. 1998 The effect of particles on wall turbulence. Intl J. Multiphase Flow 24, 359–386.CrossRefGoogle Scholar
Khalitov, D. A. & Longmire, E. K. 2002 Simultaneous two-phase PIV by two-parameter phase discrimination. Exp. Fluids 32, 252–268.Google Scholar
Khalitov, D. A. & Longmire, E. K. 2003 Effect of particle size on velocity correlations in turbulent channel flow. In Proceedings of the 4th ASME/FED and JSME Joint Fluids Conference, July 6–10, Honolulu, Hawaii.CrossRefGoogle Scholar
Kiger, K. T. & Pan, C. 2002 Suspension and turbulence modification effects of solid particulates on a horizontal turbulent channel flow. J. Turbul. 3, 1–21.CrossRefGoogle Scholar
Krishnan, G. P. & Leighton, D. T. 1995 Inertial lift on a moving sphere in contact with a plane wall in a shear flow. Phys. Fluids 7, 2538–2545.Google Scholar
Kurose, R. & Komori, S. 1999 Drag and lift forces on a rotating sphere in a linear shear flow. J. Fluid Mech. 384, 183–206.Google Scholar
Lee, H. & Balachandar, S. 2010 Drag and lift forces on a spherical particle moving on a wall in a shear flow at finite $Re$. J. Fluid Mech. 657, 89–125.CrossRefGoogle Scholar
Lee, H. & Balachandar, S. 2012 Critical shear stress for incipient motion of a particle on a rough bed. J. Geophys. Res. 117, F01026.Google Scholar
Lee, H., Ha, M. Y. & Balachandar, S. 2011 Rolling/sliding of a particle on a flat wall in a linear shear flow at finite Re. Intl J. Multiphase Flow 37, 108–124.CrossRefGoogle Scholar
Leighton, D. T. & Acrivos, A. 1985 The lift on a small sphere touching a plane in the presence of a simple shear flow. Z. Angew. Math. Phys. 36, 174–178.CrossRefGoogle Scholar
Lelouvetel, J., Bigillon, F., Doppler, D., Vinkovic, I. & Champagne, J.-Y. 2009 Experimental investigation of ejections and sweeps involved in particle suspension. Water Resour. Res. 45, W02416.CrossRefGoogle Scholar
Lu, S. S. & Willmarth, W. W. 1973 Measurement of the structure of the Reynolds stress in a turbulent boundary layer. J. Fluid Mech. 60, 481–511.Google Scholar
Marchioli, C. & Soldati, A. 2002 Mechanisms for particle transfer and segregation in a turbulent boundary layer. J. Fluid Mech. 468, 283–315.CrossRefGoogle Scholar
Mollinger, A. M. & Nieuwstadt, F. T. M. 1996 Measurement of the lift force on a particle fixed to the wall in the viscous sublayer of a fully developed turbulent boundary layer. J. Fluid Mech. 316, 285–306.Google Scholar
Munro, R. J., Bethke, N. & Dalziel, S. B. 2009 Sediment resuspension and erosion by vortex rings. Phys. Fluids 21, 046601.Google Scholar
Nalpanis, P., Hunt, J. C. R. & Barrett, C. F. 1993 Saltating particles over flat beds. J. Fluid Mech. 251, 661–685.Google Scholar
Nezu, I. & Azuma, R. 2004 Turbulence characteristics and interaction between particles and fluid in particle-laden open channel flows. J. Hydraul. Engng ASCE 988–1001.Google Scholar
Nicholson, K. W. 1988 A review of particle resuspension. Atmos. Environ. 22, 2639–2651.Google Scholar
Niño, Y. & Garcia, M. H. 1996 Experiments on particle–turbulence interactions in the near-wall region of an open channel flow: implications for sediment transport. J. Fluid Mech. 326, 285–319.Google Scholar
Phillips, M. 1980 A force balance model for particle entrainment into a fluid stream. J. Phys. D 13, 221–233.CrossRefGoogle Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Portela, L. M. & Oliemans, R. V. A. 2003 Eulerian–Lagrangian DNS/LES of particle–turbulence interactions in wall-bounded flows. Intl J. Numer. Meth. Fluids 43, 1045–1065.Google Scholar
Raffel, M., Willert, C. E., Wereley, S. T. & Kompenhans, J. 2007 Particle Image Velocimetry: A Particle Guide, 2nd edn. Springer.CrossRefGoogle Scholar
Reeks, M. W., Reed, J. & Hall, D. 1988 On the resuspension of small particles by a turbulent flow. J. Phys. D 21, 574–589.Google Scholar
Righetti, M. & Romano, G. P. 2004 Particle–fluid interactions in a plane near-wall turbulent flow. J. Fluid Mech. 505, 93–121.Google Scholar
Robinson, S. K. 1991 Coherent motions in turbulent boundary layers. Annu. Rev. Fluid Mech. 23, 601–639.Google Scholar
Rubinow, S. & Keller, J. 1961 The transverse force on a spinning sphere moving in a viscous fluid. J. Fluid Mech. 11, 447–459.Google Scholar
Saffman, P. G. 1965 The lift on a small sphere in a slow shear flow. J. Fluid Mech. 22, 385–400. Corrigendum 1968 J. Fluid Mech. 31, 624.Google Scholar
Sato, Y., Fukuichi, U. & Hishida, K. 2000 Effect of inter-particle spacing on turbulence modulation by Lagrangian PIV. Intl J. Heat Fluid Flow 21, 554–561.Google Scholar
Schlichting, H. & Gersten, K. 2003 Boundary-Layer Theory, 8th edn. Springer.Google Scholar
Schmeeckle, M. W., Nelson, J. M. & Shreve, R. L. 2007 Forces on stationary particles in near-bed turbulent flows. J. Geophys. Res. 112, F02003.Google Scholar
Sheng, J., Malkiel, E. & Katz, J. 2009 Buffer layer structures associated with extreme wall stress events in a smooth wall turbulent boundary layer. J. Fluid Mech. 633, 17–60.Google Scholar
Shields, A. 1936 a Anwendung der Aehnlichkeitsmechanik und der Turbulenzforschung auf die Geschiebebewegung. Mitteilungen der Preussischen Versuchsanstalt für Wasserbau und Schiffbau, Heft 26, Berlin (in German).Google Scholar
Shields, A. 1936 b Application of similarity principles and turbulence research to bed-load movement. Hydrodynamics Laboratory Publication 167, US Department of Agriculture, Soil Conservation Service Cooperative Laboratory, California Institute of Technology.Google Scholar
Soldati, A. 2005 Particles turbulence interactions in boundary layers. Z. Angew. Math. Mech. 85, 683–699.Google Scholar
Soldati, A. & Marchioli, C. 2009 Physics and modeling of turbulent particle deposition and entrainment: review of a systematic study. Intl J. Multiphase Flow 35, 827–839.Google Scholar
Sumer, B. M. & Deigaard, R. 1981 Particle motions near the bottom in turbulent flow in an open channel. Part 2. J. Fluid Mech. 109, 311–337.Google Scholar
Sumer, B. M. & Oguz, B. 1978 Particle motions near the bottom in turbulent flow in an open channel. J. Fluid Mech. 86, 109–127.Google Scholar
Sutherland, A. J. 1967 Proposed mechanism for sediment entrainment by turbulent flows. J. Geophys. Res. 72, 6183–6194.Google Scholar
Sweeney, L. G. & Finlay, W. H. 2007 Lift and drag forces on a sphere attached to a wall in a Blasius boundary layer. J. Aerosol Sci. 38, 131–135.CrossRefGoogle Scholar
Takemura, F. & Magnaudet, J. 2003 The transverse force on clean and contaminated bubbles rising near a vertical wall at moderate Reynolds number. J. Fluid Mech. 495, 235–253.Google Scholar
Tanière, A., Oesterlé, B. & Monnier, J. C. 1997 On the behaviour of solid particles in a horizontal boundary layer with turbulence and saltation effects. Exp. Fluids 23, 463–471.Google Scholar
Vasseur, P. & Cox, R. G. 1977 The lateral migration of spherical particles sedimenting in a stagnant bounded fluid. J. Fluid Mech. 80, 561–591.Google Scholar
White, S. J. 1970 Plane bed thresholds of fine grained sediments. Nature 228, 152–153.Google Scholar
White, B. R. & Schulz, J. C. 1977 Magnus effect in saltation. J. Fluid Mech. 81, 497–512.Google Scholar
Wiberg, P. L. & Smith, J. D. 1985 A theoretical model for saltating grains in water. J. Geophys. Res. 90, 7341–7354.Google Scholar
Willmarth, W. W. & Lu, S. S. 1972 Structure of the Reynolds stress near the wall. J. Fluid Mech. 55, 65–92.Google Scholar
Wu, Y. & Christensen, K. T. 2006 Population trends of spanwise vortices in wall turbulence. J. Fluid Mech. 568, 55–76.Google Scholar
Yamamoto, Y., Potthoff, M., Tanaka, T., Kajishima, T. & Tsuji, Y. 2001 Large-eddy simulation of turbulent gas-particle flow in a vertical channel: effect of considering inter-particle collisions. J. Fluid Mech. 442, 303–334.Google Scholar
Zeng, L., Balachandar, S. & Fischer, P. 2005 Wall-induced forces on a rigid sphere at finite Reynolds number. J. Fluid Mech. 536, 1–25.Google Scholar
Zeng, L., Balachandar, S., Fischer, P. & Najjar, F. 2008 Interactions of a stationary finite-sized particle with wall turbulence. J. Fluid Mech. 594, 271–305.Google Scholar
Zeng, L., Najjar, F., Balachandar, S. & Fischer, P. 2009 Forces on a finite-sized particle located close to a wall in a linear shear flow. Phys. Fluids 21, 033302.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar
Ziskind, G., Fichman, M. & Gutfinger, C. 1995 Resuspension of particulates from surfaces to turbulent flows: review and analysis. J. Aerosol Sci. 26, 613–644.Google Scholar