Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-01-12T23:24:49.706Z Has data issue: false hasContentIssue false
  • English
  • Français

The spatial structure of the logarithmic region in very-high-Reynolds-number rough wall turbulent boundary layers

Published online by Cambridge University Press:  26 October 2018

Michael Heisel Open the ORCID record for Michael Heisel [Opens in a new window] ,
Teja Dasari ,
Yun Liu ,
Jiarong Hong Open the ORCID record for Jiarong Hong [Opens in a new window] ,
Filippo Coletti  and
Michele Guala
Michael Heisel*
Affiliation:
St Anthony Falls Laboratory, University of Minnesota, Minneapolis, MN 55414, USA Department of Civil, Environmental, and Geo- Engineering, University of Minnesota, Minneapolis, MN 55455, USA
Teja Dasari
Affiliation:
St Anthony Falls Laboratory, University of Minnesota, Minneapolis, MN 55414, USA Department of Mechanical Engineering, University of Minnesota, Minneapolis, MN 55455, USA
Yun Liu
Affiliation:
Department of Mechanical and Civil Engineering, Purdue University Northwest, Westville, IN 46391, USA
Jiarong Hong
Affiliation:
St Anthony Falls Laboratory, University of Minnesota, Minneapolis, MN 55414, USA Department of Mechanical Engineering, University of Minnesota, Minneapolis, MN 55455, USA
Filippo Coletti
Affiliation:
St Anthony Falls Laboratory, University of Minnesota, Minneapolis, MN 55414, USA Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA
Michele Guala
Affiliation:
St Anthony Falls Laboratory, University of Minnesota, Minneapolis, MN 55414, USA Department of Civil, Environmental, and Geo- Engineering, University of Minnesota, Minneapolis, MN 55455, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

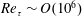Using super-large-scale particle image velocimetry (SLPIV), we investigate the spatial structure of the near-wall region in the fully rough atmospheric surface layer with Reynolds number $Re_{\unicode[STIX]{x1D70F}}\sim O(10^{6})$. The field site consists of relatively flat, snow-covered farmland, allowing for the development of a fully rough turbulent boundary layer under near-neutral thermal stability conditions. The imaging field of view extends from 3 m to 19 m above the ground and captures the top of the roughness sublayer and the bottom of an extensive logarithmic region. The SLPIV technique uses natural snowfall as seeding particles for the flow imaging. We demonstrate that SLPIV provides reliable measurements of first- and second-order velocity statistics in the streamwise and wall-normal directions. Our results in the logarithmic region show that the structural features identified in laboratory studies are similarly present in the atmosphere. Using instantaneous vector fields and two-point correlation analysis, we identify vortex structures sharing the signature of hairpin vortex packets. We also evaluate the zonal structure of the boundary layer by tracking uniform momentum zones (UMZs) and the shear interfaces between UMZs in space and time. Statistics of the UMZs and shear interfaces reveal the role of the zonal structure in determining the mean and variance profiles. The velocity difference across the shear interfaces scales with the friction velocity, in agreement with previous studies, and the size of the UMZs scales with wall-normal distance, in agreement with the attached eddy framework.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 857 , 25 December 2018 , pp. 704 - 747
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19 (4), 041301.Google Scholar
Adrian, R. J., Christensen, K. T. & Liu, Z.-C. 2000a Analysis and interpretation of instantaneous turbulent velocity fields. Exp. Fluids 29 (3), 275–290.Google Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000b Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2006 Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 561, 329–358.Google Scholar
Balakuma, B. J. & Adrian, R. J. 2007 Large- and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. Lond. A 365, 665–681.Google Scholar
Brandes, E. A., Ikeda, K., Zhang, G., Schönhuber, M. & Rasmussen, R. M. 2007 A statistical and physical description of hydrometeor distributions in Colorado snowstorms using a video disdrometer. J. Appl. Meteorol. Climatol. 46 (5), 634–650.Google Scholar
Brown, G. L. & Roshko, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64 (4), 775–816.Google Scholar
Carter, D. W. & Coletti, F. 2017 Scale-to-scale anisotropy in homogeneous turbulence. J. Fluid Mech. 827, 250–284.Google Scholar
Chauhan, K., Hutchins, N., Monty, J. P. & Marusic, I. 2012 Structure inclination angles in the convective atmospheric surface layer. Boundary-Layer Meteorol. 147 (1), 41–50.Google Scholar
Chini, G. P., Montemuro, C., White, C. M. & Klewicki, J. C. 2017 A self-sustaining process model of inertial layer dynamics in high Reynolds number turbulent wall flows. Phil. Trans. R. Soc. Lond. A 375, 20160090.Google Scholar
Christensen, K. T. & Adrian, R. J. 2001 Statistical evidence of hairpin vortex packets in wall turbulence. J. Fluid Mech. 431, 433–443.Google Scholar
Clarke, R. H., Dyer, A. J., Brokk, R. R., Reid, D. G. & Troup, A. J.1971 The Wangara experiment: boundary-layer data. Technical Paper 19, CSIRO Division of Meteorological Physics.Google Scholar
Corrsin, S.1958 Local isotropy in turbulent shear flow. NACA Research Memo. 58B11.Google Scholar
Crowe, C. T., Schwarzkopf, J. D., Sommerfeld, M. & Tsuji, Y. 1998 Multiphase Flows with Droplets and Particles. CRC Press.Google Scholar
Dennis, D. J. & Nickels, T. B. 2011 Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 1. Vortex packets. J. Fluid Mech. 673, 180–217.Google Scholar
Dong, S., Lozano-Durán, A., Sekimoto, A. & Jiménez, J. 2017 Coherent structures in statistically stationary homogeneous shear turbulence. J. Fluid Mech. 816, 167–208.Google Scholar
Eisma, J., Westerweel, G., Ooms, G. & Elsinga, G. E. 2015 Interfaces and internal layers in a turbulent boundary layer. Phys. Fluids 27 (5), 055103.Google Scholar
Elsinga, G. E. & Marusic, I. 2010 Universal aspects of small-scale motions in turbulence. J. Fluid Mech. 662, 514–539.Google Scholar
Etter, R. J., Cutbirth, J. M., Ceccio, S. L., Dowling, D. R. & Perlin, M. 2005 High Reynolds number experimentation in the US Navy’s William B. Morgan Large Cavitation Channel. Meas. Sci. Technol. 16 (9), 1701–1709.Google Scholar
Flack, K. A., Schultz, M. P. & Connelly, J. S. 2007 Examination of a critical roughness height for outer layer similarity. Phys. Fluids 19 (9), 095104.Google Scholar
Frank, J. M., Massman, W. J. & Ewers, B. E. 2013 Underestimates of sensible heat flux due to vertical velocity measurement errors in non-orthogonal sonic anemometers. Agric. Forest Meteorol. 171–172, 72–81.Google Scholar
Ganapathisubramani, B., Hutchins, N., Hambleton, W. T., Longmire, E. K. & Marusic, I. 2005 Investigation of large-scale coherence in a turbulent boundary layer using two-point correlations. J. Fluid Mech. 524, 57–80.Google Scholar
Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478, 35–46.Google Scholar
Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2006 Experimental investigation of vortex properties in a turbulent boundary layer. Phys. Fluids 18 (5), 055105.Google Scholar
Garratt, J. R. 1994 The Atmospheric Boundary Layer. Cambridge University Press.Google Scholar
Graftieaux, L., Michard, M. & Grosjean, N. 2001 Combining PIV, POD and vortex identification algorithms for the study of unsteady turbulent swirling flows. Meas. Sci. Technol. 12 (9), 1422–1429.Google Scholar
Grant, A. L. M. & Watkins, R. D. 1989 Errors in turbulence measurements with a sonic anemometer. Boundary-Layer Meteorol. 46 (1–2), 181–194.Google Scholar
Grass, A. J. 1971 Structural features of turbulent flow over smooth and rough boundaries. J. Fluid Mech. 50 (2), 233–255.Google Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.Google Scholar
Guala, M., Metzger, M. & McKeon, B. J. 2011 Interactions within the turbulent boundary layer at high Reynolds number. J. Fluid Mech. 666, 573–604.Google Scholar
Guala, M., Tomkins, C. D., Christensen, K. T. & Adrian, R. J. 2012 Vortex organization in a turbulent boundary layer overlying sparse roughness elements. J. Hydraul. Res. 50 (5), 465–481.Google Scholar
Head, M. R. & Bandyopadhyay, P. 1981 New aspects of turbulent boundary-layer structure. J. Fluid Mech. 107, 297–338.Google Scholar
Hearst, R. J. & Ganapathisubramani, B. 2015 Quantification and adjustment of pixel-locking in particle image velocimetry. Exp. Fluids 56, 191.Google Scholar
Herpin, S., Stanislas, M., Foucaut, J. M. & Coudert, S. 2013 Influence of the Reynolds number on the vortical structures in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 716, 5–50.Google Scholar
Heymsfield, A. J., Bansemer, A., Schmitt, C., Twohy, C. & Poellot, M. R. 2004 Effective ice particle densities derived from aircraft data. J. Atmos. Sci. 61 (9), 982–1003.Google Scholar
Högström, U., Hunt, J. C. R. & Smedman, A. 2002 Theory and measurements for turbulence spectra and variances in the atmospheric neutral surface layer. Boundary-Layer Meteorol. 103 (1), 101–124.Google Scholar
Hommema, S. E. & Adrian, R. J. 2003 Packet structure of surface eddies in the atmospheric boundary layer. Boundary-Layer Meteorol. 106 (1), 147–170.Google Scholar
Hong, J., Dasari, T., Wu, Y. & Liu, Y. 2017 Velocity field and coherent structures in the near wake of a utility-scale wind turbine. In Bull. 70th Annu. Meeting of the APS Division of Fluid Dynamics, American Physical Society.Google Scholar
Hong, J., Katz, J. & Schultz, M. P. 2011 Near-wall turbulence statistics and flow structures over three-dimensional roughness in a turbulent channel flow. J. Fluid Mech. 667, 1–37.Google Scholar
Hong, J., Toloui, M., Chamorro, L. P., Guala, M., Howard, K. B., Riley, S., Tucker, J. & Sotiropoulos, F. 2014 Natural snowfall reveals large-scale flow structures in the wake of a 2.5-MW wind turbine. Nature Commun. 5, 4216.Google Scholar
Hunt, J. C. R. & Carlotti, P. 2001 Statistical structure at the wall of the high Reynolds number turbulent boundary layer. Flow Turbul. Combust. 66 (4), 453–475.Google Scholar
Hunt, J. C. R., Ishihara, T., Worth, N. A. & Kaneda, Y. 2014 Thin shear layer structures in high Reynolds number turbulence. Flow Turbul. Combust. 92 (3), 607–649.Google Scholar
Hutchins, N., Chauhan, K., Marusic, I., Monty, J. P. & Klewicki, J. C. 2012 Towards reconciling the large-scale structure of turbulent boundary layers in the atmosphere and laboratory. Boundary-Layer Meteorol. 145 (2), 273–306.Google Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Ishihara, T., Kaneda, Y. & Hunt, J. C. R. 2013 Thin shear layers in high Reynolds number turbulence: DNS results. Flow Turbul. Combust. 91 (4), 895–929.Google Scholar
Jiménez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36 (1), 173–196.Google Scholar
Jiménez, J. 2018 Coherent structures in wall-bounded turbulence. J. Fluid Mech. 842, P1.Google Scholar
Kaimal, J. C. & Finnigan, J. J. 1994 Atmospheric Boundary Layer Flows. Oxford University Press.Google Scholar
von Kármán, T.1931 Mechanical similitude and turbulence. NACA Tech. Memo. 611.Google Scholar
Krogstad, P. A., Antonia, R. A. & Browne, L. W. B. 1992 Comparison between rough- and smooth-wall turbulent boundary layers. J. Fluid Mech. 245, 599–617.Google Scholar
Kunkel, G. J. & Marusic, I. 2006 Study of the near-wall-turbulent region of the high-Reynolds-number boundary layer using an atmospheric flow. J. Fluid Mech. 548, 375–402.Google Scholar
Kwon, Y. S., Philip, J., de Silva, C. M., Hutchins, N. & Monty, J. P. 2014 The quiescent core of turbulent channel flow. J. Fluid Mech. 751, 228–254.Google Scholar
Laskari, A., de Kat, R., Hearst, R. J. & Ganapathisubramani, B. 2018 Time evolution of uniform momentum zones in a turbulent boundary layer. J. Fluid Mech. 842, 554–590.Google Scholar
Lee, J. H. & Sung, H. J. 2011 Very-large-scale motions in a turbulent boundary layer. J. Fluid Mech. 673, 80–120.Google Scholar
Liu, H.-Y., Bo, T.-L. & Liang, Y.-R. 2017 The variation of large-scale structure inclination angles in high Reynolds number atmospheric surface layers. Phys. Fluids 29, 035104.Google Scholar
Makkonen, L., Lehtonen, P. & Helle, L. 2001 Anemometry in icing conditions. J. Atmos. Ocean. Technol. 18, 1457–1469.Google Scholar
Marusic, I. 2001 On the role of large-scale structures in wall turbulence. Phys. Fluids 13 (3), 735–743.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716 (R3), 1–11.Google Scholar
Meinhart, C. D. & Adrian, R. J. 1995 On the existence of uniform momentum zones in a turbulent boundary layer. Phys. Fluids 7 (4), 694–696.Google Scholar
Metzger, M. & Klewicki, J. C. 2001 A comparative study of near-wall turbulence in high and low Reynolds number boundary layers. Phys. Fluids 13 (3), 692–701.Google Scholar
Metzger, M., McKeon, B. J. & Holmes, H. 2007 The near-neutral atmospheric surface layer: turbulence and non-stationarity. Phil. Trans. R. Soc. A 365, 859–876.Google Scholar
Morrill-Winter, C., Squire, D. T., Klewicki, J. C., Hutchins, N., Schultz, M. P. & Marusic, I. 2017 Reynolds number and roughness effects on turbulent stresses in sandpaper roughness boundary layers. Phys. Rev. Fluids 2 (5), 054608.Google Scholar
Morris, S. C., Stolpa, S. R., Slaboch, P. E. & Klewicki, J. C. 2007 Near-surface particle image velocimetry measurements in a transitionally rough-wall atmospheric boundary layer. J. Fluid Mech. 580, 319–338.Google Scholar
Na, Y., Hanratty, T. J. & Liu, Z. C. 2001 The use of DNS to define stress producing events for turbulent flow over a smooth wall. Flow Turbul. Combust. 66 (4), 495–512.Google Scholar
Nemes, A., Dasari, T., Hong, J., Guala, M. & Coletti, F. 2017 Snowflakes in the atmospheric surface layer: observation of particle–turbulence dynamics. J. Fluid Mech. 814, 592–613.Google Scholar
Nemes, A., Jacono, D. L., Blackburn, H. M. & Sheridan, J. 2015 Mutual inductance of two helical vortices. J. Fluid Mech. 774, 298–310.Google Scholar
Nickels, T. B., Marusic, I., Hafez, S. & Chong, M. S. 2005 Evidence of the k 1 -1 law in a high-Reynolds-number turbulent boundary layer. Phys. Rev. Lett. 95 (7), 074501.Google Scholar
Nickels, T. B., Marusic, I., Hafez, S., Hutchins, N. & Chong, M. S. 2007 Some predictions of the attached eddy model for a high Reynolds number boundary layer. Phil. Trans. R. Soc. Lond. A 365, 807–822.Google Scholar
Nikuradse, J.1933 Laws of flow in rough pipes. NACA Tech. Memo. 1292.Google Scholar
Offen, G. R. & Kline, S. J. 1974 Combined dye-streak and hydrogen-bubble visual observations of a turbulent boundary layer. J. Fluid Mech. 62 (2), 223–239.Google Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.Google Scholar
Perry, A. E. & Marusic, I. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 1. Extension of the attached eddy hypothesis. J. Fluid Mech. 298, 361–388.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Prandtl, L. 1925 Bericht über Untersuchungen zur ausgebildeten Turbulenz. ZAMM. Z. Angew. Math. Mech. 5, 136–139.Google Scholar
Priyadarshana, P. J. A., Klewicki, J. C., Treat, S. & Foss, J. F. 2007 Statistical structure of turbulent-boundary-layer velocity–vorticity products at high and low Reynolds numbers. J. Fluid Mech. 570, 307–346.Google Scholar
Pruppacher, H. R. & Klett, J. D. 1997 Microphysics of Clouds and Precipitation. Springer.Google Scholar
Raupach, M. R., Antonia, R. A. & Rajagopalan, S. 1991 Rough-wall turbulent boundary layers. Appl. Mech. Rev. 44 (1), 1–25.Google Scholar
Roth, G. I. & Katz, J. 2001 Five techniques for increasing the speed and accuracy of PIV interrogation. Meas. Sci. Technol. 12 (3), 238–245.Google Scholar
Saddoughi, S. G. & Veeravalli, S. V. 1994 Local isotropy in turbulent boundary layers at high Reynolds number. J. Fluid Mech. 268, 333–372.Google Scholar
Schultz, M. P. & Flack, K. A. 2007 The rough-wall turbulent boundary layer from the hydraulically smooth to the fully rough regime. J. Fluid Mech. 580, 381–405.Google Scholar
Shen, X. & Warhaft, Z. 2000 The anisotropy of the small scale structure in high Reynolds number (r 𝜆 ∼ 1000) turbulent shear flow. Phys. Fluids 12 (11), 2976.Google Scholar
de Silva, C. M., Hutchins, N. & Marusic, I. 2016 Uniform momentum zones in turbulent boundary layers. J. Fluid Mech. 786, 309–331.Google Scholar
de Silva, C. M., Philip, J., Hutchins, N. & Marusic, I. 2017 Interfaces of uniform momentum zones in turbulent boundary layers. J. Fluid Mech. 820, 451–478.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High–Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43 (1), 353–375.Google Scholar
Squire, D. T., Morrill-Winter, C., Hutchins, N., Marusic, I., Schultz, M. P. & Klewicki, J. C. 2016a Smooth- and rough-wall boundary layer structure from high spatial range particle image velocimetry. Phys. Rev. Fluids 1 (6), 064402.Google Scholar
Squire, D. T., Morrill-Winter, C., Hutchins, N., Schultz, M. P., Klewicki, J. C. & Marusic, I. 2016b Comparison of turbulent boundary layers over smooth and rough surfaces up to high Reynolds numbers. J. Fluid Mech. 795, 210–240.Google Scholar
Stull, R. B. 1988 An Introduction to Boundary Layer Meteorology. Kluwer Academic Publishers.Google Scholar
Sutton, O. G. 1953 Micrometeorology. McGraw-Hill.Google Scholar
Theodorsen, T. 1952 Mechanism of turbulence. In Proc. Midwestern Conf. Fluid Mech, Ohio State University.Google Scholar
Thompson, G., Field, P. R., Rasmussen, R. M. & Hall, W. D. 2008 Explicit forecasts of winter precipitation using an improved bulk microphysics scheme. Part II. Implementation of a new snow parameterization. Mon. Weath. Rev. 136 (12), 5095–5115.Google Scholar
Tieleman, H. W. 2008 Strong wind observations in the atmospheric surface layer. J. Wind Engng Ind. Aerodyn. 96 (1), 41–77.Google Scholar
Toloui, M., Riley, S., Hong, J., Howard, K. B., Chamorro, L. P., Guala, M. & Tucker, J. 2014 Measurement of atmospheric boundary layer based on super-large-scale particle image velocimetry using natural snowfall. Exp. Fluids 55 (5), 1737.Google Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, vol. 2. Cambridge University Press.Google Scholar
Vanderwel, C. & Tavoularis, S. 2011 Coherent structures in uniformly sheared turbulent flow. J. Fluid Mech. 689, 434–464.Google Scholar
Volino, R. J., Schultz, M. P. & Flack, K. A. 2007 Turbulence structure in rough- and smooth-wall boundary layers. J. Fluid Mech. 592, 263–293.Google Scholar
Wallace, J. M., Eckelmann, H. & Brodkey, R. S. 1972 The wall region in turbulent shear flow. J. Fluid Mech. 54 (1), 39–48.Google Scholar
Wang, G. & Zheng, X. 2016 Very large scale motions in the atmospheric surface layer: a field investigation. J. Fluid Mech. 802, 464–489.Google Scholar
Wei, L., Elsinga, G. E., Brethouwer, G., Schlatter, P. & Johansson, A. V. 2014 Universality and scaling phenomenology of small-scale turbulence in wall-bounded flows. Phys. Fluids 26 (3), 035107.Google Scholar
Westerweel, J. & Scarano, F. 2005 Universal outlier detection for PIV data. Exp. Fluids 39 (6), 1096–1100.Google Scholar
Woodcock, J. D. & Marusic, I. 2015 The statistical behaviour of attached eddies. Phys. Fluids 27 (1), 015104.Google Scholar
Wu, X. & Moin, P. 2009 Direct numerical simulation of turbulence in a nominally zero-pressure-gradient flat-plate boundary layer. J. Fluid Mech. 650, 5–41.Google Scholar
Wu, Y. & Christensen, K. T. 2006 Population trends of spanwise vortices in wall turbulence. J. Fluid Mech. 568, 55–76.Google Scholar
Zagarola, M. V., Smits, A. J., Orszag, S. A. & Yakhot, V.1996 Experiments in high Reynolds number turbulent pipe flow. AIAA Report 96-0654.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar

Heisel et al. supplementary movie

Time evolution of the vortex structure highlighted in figure 6 of the article. (left) Velocity vector field overlaid on the PIV images. The listed convective velocity is subtracted from the vectors. (middle) Color plot of the streamwise velocity. (right) Color plot of the swirling strength for vortices tracked using the methodology described in Appendix A.

Download Heisel et al. supplementary movie(Video)
Video 9.9 MB