Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T08:01:15.210Z Has data issue: false hasContentIssue false
  • English
  • Français

Spanwise velocity statistics in high-Reynolds-number turbulent boundary layers

Published online by Cambridge University Press:  02 March 2021

R. Baidya Open the ORCID record for R. Baidya [Opens in a new window] ,
J. Philip ,
N. Hutchins ,
J.P. Monty  and
I. Marusic Open the ORCID record for I. Marusic [Opens in a new window]
R. Baidya*
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria3010, Australia
J. Philip
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria3010, Australia
N. Hutchins
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria3010, Australia
J.P. Monty
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria3010, Australia
I. Marusic
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria3010, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

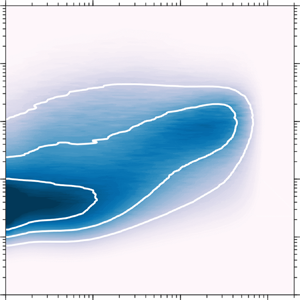
Spanwise velocity statistics from high-Reynolds-number turbulent boundary layers are reported. The dataset combines efforts spanning over a decade at the University of Melbourne to accurately capture Reynolds number ($Re$) trends for the spanwise velocity, nominally over one order of magnitude change in $Re$, using custom subminiature cross-wire probes that minimise spatial resolution effects and misalignment errors. The spanwise velocity ($v$) variance is found to exhibit an $Re$ invariant logarithmic slope in the log region, in a similar manner to the streamwise velocity ($u$), which is consistent with the existence of self-similar features within wall-bounded flows. However, unlike the $u$-variance, it appears that the logarithmic $v$-variance trend continues to extend towards the wall. The increase in the $v$-variance with $Re$ in the log region is found to be due to ‘intermediate-scale eddies’, which follow distance-from-the-wall scaling. This results in the $v$-spectrogram exhibiting a dominant energetic ridge across the intermediate-scales, a trend that is not clearly observed in the $u$-spectrogram. Other features of the $v$-spectrogram are found to be similar to the $u$-spectrogram, such as showing small-scale near-wall features that scale universally with viscous units, and the influence of large-scale $v$ signals residing in the log region that extend to the wall, resulting in a large-scale $v$ footprint in the near-wall region. The observed behaviour of the $v$-spectrogram with changing $Re$ is used to construct a model for the $v$-variance based on contributions from small-, intermediate- and large-scales, leading to a predictive tool at asymptotically high $Re$.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 913 , 25 April 2021 , A35
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abe, H., Kawamura, H. & Choi, H. 2004 Very large-scale structures and their effects on the wall shear-stress fluctuations in a turbulent channel flow up to $Re_\tau = 640$. J. Fluid Engng 126 (5), 835–843.CrossRefGoogle Scholar
Adrian, R.J., Meinhart, C.D. & Tomkins, C.D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.CrossRefGoogle Scholar
Baidya, R. 2016 Multi-component velocity measurements in turbulent boundary layers. PhD thesis, University of Melbourne.Google Scholar
Baidya, R., Philip, J., Hutchins, N., Monty, J.P. & Marusic, I. 2019 a Sensitivity of turbulent stresses in boundary layers to cross-wire probe uncertainties in the geometry and calibration procedure. Meas. Sci. Technol. 30, 085301.CrossRefGoogle Scholar
Baidya, R., Philip, J., Hutchins, N., Monty, J.P. & Marusic, I. 2019 b Spatial averaging effects on the streamwise and wall-normal velocity measurments in a wall-bounded turbulence using a cross-wire probe. Meas. Sci. Technol. 30, 085303.CrossRefGoogle Scholar
Baidya, R., Philip, J., Hutchins, N., Monty, J.P. & Marusic, I. 2017 Distance-from-the-wall scaling of turbulent motions in wall-bounded flows. Phys. Fluids 29 (2), 020712.CrossRefGoogle Scholar
Baidya, R., Philip, J., Monty, J.P., Hutchins, N. & Marusic, I. 2014 Comparisons of turbulence stresses from experiments against the attached eddy hypothesis in boundary layers. In Proceedings of the 19th Australasian Fluid Mechanics Conference (ed. H. Chowdhury & F. Alam). RMIT University.Google Scholar
Browne, L.W.B., Antonia, R.A. & Shah, D.A. 1988 Selection of wires and wire spacing for $\times$-wires. Exp. Fluids 6 (4), 286–288.CrossRefGoogle Scholar
Champagne, F.H., Sleicher, C.A. & Wehrmann, O.H. 1967 Turbulence measurements with inclined hot-wires. Part 1. Heat transfer experiments with inclined hot-wire. J. Fluid Mech. 28 (01), 153–175.CrossRefGoogle Scholar
Chauhan, K., Philip, J., de Silva, C.M., Hutchins, N. & Marusic, I. 2014 The turbulent/non-turbulent interface and entrainment in a boundary layer. J. Fluid Mech. 742, 119–151.CrossRefGoogle Scholar
Chauhan, K.A., Monkewitz, P.A. & Nagib, H.M. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41 (2), 021404.CrossRefGoogle Scholar
Chin, C., Monty, J.P. & Ooi, A. 2014 Reynolds number effects in DNS of pipe flow and comparison with channels and boundary layers. Intl J. Heat Fluid Flow 45, 33–40.CrossRefGoogle Scholar
Choi, H., Moin, P. & Kim, J. 1994 Active turbulence control for drag reduction in wall-bounded flows. J. Fluid Mech. 262, 75–110.CrossRefGoogle Scholar
Collis, D.C. & Williams, M.J. 1959 Two-dimensional convection from heated wires at low Reynolds numbers. J. Fluid Mech. 6 (3), 357–384.CrossRefGoogle Scholar
Davidson, P.A., Nickels, T.B. & Krogstad, P.-Å. 2006 The logarithmic structure function law in wall-layer turbulence. J. Fluid Mech. 550, 51–60.CrossRefGoogle Scholar
DeGraaff, D.B. & Eaton, J.K. 2000 Reynolds-number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.CrossRefGoogle Scholar
del Álamo, J.C. & Jiménez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor's approximation. J. Fluid Mech. 640, 5–26.CrossRefGoogle Scholar
del Álamo, J.C., Jiménez, J., Zandonade, P. & Moser, R.D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.CrossRefGoogle Scholar
Fernholz, H.H. & Finley, P.J. 1996 The incompressible zero-pressure-gradient turbulent boundary layer: an assessment of the data. Prog. Aerosp. Sci. 32 (4), 245–311.CrossRefGoogle Scholar
Gatti, D. & Quadrio, M. 2016 Reynolds-number dependence of turbulent skin-friction drag reduction induced by spanwise forcing. J. Fluid Mech. 802, 553–582.CrossRefGoogle Scholar
Hatton, A.P., James, D.D. & Swire, H.W. 1970 Combined forced and natural convection with low-speed air flow over horizontal cylinders. J. Fluid Mech. 42 (1), 17–31.CrossRefGoogle Scholar
Hinze, J.O. 1975 Turbulence: an Introduction to its Mechanisms and Theory. McGraw-Hill.Google Scholar
Hultmark, M., Vallikivi, M., Bailey, S.C.C. & Smits, A.J. 2012 Turbulent pipe flow at extreme Reynolds numbers. Phys. Rev. Lett. 108 (9), 094501.CrossRefGoogle ScholarPubMed
Hurst, E., Yang, Q. & Chung, Y.M. 2014 The effect of Reynolds number on turbulent drag reduction by streamwise travelling waves. J. Fluid Mech. 759, 28–55.CrossRefGoogle Scholar
Hutchins, N., Chauhan, K., Marusic, I., Monty, J. & Klewicki, J. 2012 Towards reconciling the large-scale structure of turbulent boundary layers in the atmosphere and laboratory. Boundary-Layer Meteorol. 145 (2), 273–306.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007 a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007 b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365, 647–664.Google ScholarPubMed
Hutchins, N., Nickels, T.B., Marusic, I. & Chong, M.S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.CrossRefGoogle Scholar
Hwang, J. & Sung, H.J. 2018 Wall-attached structures of velocity fluctuations in a turbulent boundary layer. J. Fluid Mech. 856, 958–983.CrossRefGoogle Scholar
Jeong, J., Hussain, F., Schoppa, W. & Kim, J. 1997 Coherent structures near the wall in a turbulent channel flow. J. Fluid Mech. 332, 185–214.CrossRefGoogle Scholar
Jiménez, J. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225, 213–240.CrossRefGoogle Scholar
Karniadakis, G.E. & Choi, K.S. 2003 Mechanisms on transverse motions in turbulent wall flows. Annu. Rev. Fluid Mech. 35 (1), 45–62.CrossRefGoogle Scholar
Kim, H.T., Kline, S.J. & Reynolds, W.C. 1971 The production of turbulence near a smooth wall in a turbulent boundary layer. J. Fluid Mech. 50 (1), 133–160.CrossRefGoogle Scholar
Klewicki, J.C., Saric, W.S., Marusic, I. & Eaton, J.K. 2007 Wall-bounded flows. In Springer Handbook of Experimental Fluid Mechanics (ed. C. Tropea, A.L. Yarin & J.F. Foss), vol. 1, chap. 5.2, pp. 229–286. Springer.Google Scholar
Kwon, Y.S., Hutchins, N. & Monty, J.P. 2016 On the use of the Reynolds decomposition in the intermittent region of turbulent boundary layers. J. Fluid Mech. 794, 5–16.CrossRefGoogle Scholar
Laufer, J. 1954 The structure of turbulence in fully developed pipe flow. Tech. Rep. NACA-TR-1174. National Advisory Committee for Aeronautics.Google Scholar
Lee, M. & Moser, R.D. 2015 Direct numerical simulation of turbulent channel flow up to $Re_\tau \approx 5200$. J. Fluid Mech. 774, 395–415.CrossRefGoogle Scholar
Marusic, I., Chauhan, K.A., Kulandaivelu, V. & Hutchins, N. 2015 Evolution of zero-pressure-gradient boundary layers from different tripping conditions. J. Fluid Mech. 783, 379–411.CrossRefGoogle Scholar
Marusic, I. & Monty, J.P. 2019 Attached eddy model of wall turbulence. Annu. Rev. Fluid Mech. 51, 49–74.CrossRefGoogle Scholar
Marusic, I., Monty, J.P., Hultmark, M. & Smits, A.J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, 716.CrossRefGoogle Scholar
Marusic, I., Uddin, A.K.M. & Perry, A.E. 1997 Similarity law for the streamwise turbulence intensity in zero-pressure-gradient turbulent boundary layers. Phys. Fluids 9 (12), 3718–3726.CrossRefGoogle Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.CrossRefGoogle Scholar
Mehrez, A., Philip, J., Yamamoto, Y. & Tsuji, Y. 2019 Pressure and spanwise velocity fluctuations in turbulent channel flows: logarithmic behavior of moments and coherent structures. Phys. Rev. Fluids 4 (4), 044601.CrossRefGoogle Scholar
Meneveau, C. & Marusic, I. 2013 Generalized logarithmic law for high-order moments in turbulent boundary layers. J. Fluid Mech. 719, R1.CrossRefGoogle Scholar
Millikan, C.B. 1938 A critical discussion of turbulent flows in channels and circular tubes. In Proceedings of the Fifth International Congress for Applied Mechanics (ed. J.P. den Hartog & H. Peters), pp. 386–392. Wiley.Google Scholar
Monkewitz, P.A. & Nagib, H.M. 2015 Large-Reynolds-number asymptotics of the streamwise normal stress in zero-pressure-gradient turbulent boundary layers. J. Fluid Mech. 783, 474–503.CrossRefGoogle Scholar
Monty, J.P. & Chong, M.S. 2009 Turbulent channel flow: comparison of streamwise velocity data from experiments and direct numerical simulation. J. Fluid Mech. 633, 461–474.CrossRefGoogle Scholar
Morrill-Winter, C., Klewicki, J., Baidya, R. & Marusic, I. 2015 Temporally optimized spanwise vorticity sensor measurements in turbulent boundary layers. Exp. Fluids 56 (12), 216.CrossRefGoogle Scholar
Morrill-Winter, C., Philip, J. & Klewicki, J. 2017 An invariant representation of mean inertia: theoretical basis for a log law in turbulent boundary layers. J. Fluid Mech. 813, 594–617.CrossRefGoogle Scholar
Nickels, T.B. & Marusic, I. 2001 On the different contributions of coherent structures to the spectra of a turbulent round jet and a turbulent boundary layer. J. Fluid Mech. 448, 367–385.CrossRefGoogle Scholar
Nickels, T.B., Marusic, I., Hafez, S. & Chong, M.S. 2005 Evidence of the $k_1^{-1}$ law in a high-Reynolds-number turbulent boundary layer. Phys. Rev. Lett. 95 (7), 074501.CrossRefGoogle Scholar
Örlü, R. & Schlatter, P. 2013 Comparison of experiments and simulations for zero pressure gradient turbulent boundary layers at moderate Reynolds numbers. Exp. Fluids 54 (6), 1547.CrossRefGoogle Scholar
Perry, A.E. & Abell, C.J. 1975 Scaling laws for pipe-flow turbulence. J. Fluid Mech. 67 (2), 257–271.CrossRefGoogle Scholar
Perry, A.E. & Chong, M.S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.CrossRefGoogle Scholar
Perry, A.E., Henbest, S. & Chong, M.S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.CrossRefGoogle Scholar
Philip, J., Hutchins, N., Monty, J.P. & Marusic, I. 2013 a Spatial averaging of velocity measurements in wall-bounded turbulence: single hot-wires. Meas. Sci. Technol. 24 (11), 115301.CrossRefGoogle Scholar
Philip, J., Baidya, R., Hutchins, N., Monty, J.P. & Marusic, I. 2013 b Spatial averaging of streamwise and spanwise velocity measurements in wall-bounded turbulence using $\vee$- and $\times$-probes. Meas. Sci. Technol. 24 (11), 115302.CrossRefGoogle Scholar
Quadrio, M. 2011 Drag reduction in turbulent boundary layers by in-plane wall motion. Phil. Trans. R. Soc. Lond. A 369 (1940), 1428–1442.Google ScholarPubMed
Samie, M., Marusic, I., Hutchins, N., Fu, M.K., Fan, Y., Hultmark, M. & Smits, A.J. 2018 Fully resolved measurements of turbulent boundary layer flows up to $Re_\tau = 20\,000$. J. Fluid Mech. 851, 391–415.CrossRefGoogle Scholar
Schlatter, P. & Örlü, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.CrossRefGoogle Scholar
Sillero, J.A., Jiménez, J. & Moser, R.D. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to $\delta ^+ \approx 2000$. Phys. Fluids 25 (10), 105102.CrossRefGoogle Scholar
Sillero, J.A., Jiménez, J. & Moser, R.D. 2014 Two-point statistics for turbulent boundary layers and channels at Reynolds numbers up to $\delta ^+ \approx 2000$. Phys. Fluids 26 (10), 105109.CrossRefGoogle Scholar
de Silva, C.M., Woodcock, J.D., Hutchins, N. & Marusic, I. 2016 Influence of spatial exclusion on the statistical behavior of attached eddies. Phys. Rev. Fluids 1 (2), 022401.CrossRefGoogle Scholar
Smits, A.J., McKeon, B.J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.CrossRefGoogle Scholar
Talluru, K.M., Baidya, R., Hutchins, N. & Marusic, I. 2014 Amplitude modulation of all three velocity components in turbulent boundary layers. J. Fluid Mech. 746, R1.CrossRefGoogle Scholar
Taylor, G.I. 1938 The spectrum of turbulence. Proc. R. Soc. Lond. A 164 (919), 476–490.Google Scholar
Townsend, A.A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Wei, T., Fife, P., Klewicki, J. & McMurtry, P. 2005 Properties of the mean momentum balance in turbulent boundary layer, pipe and channel flows. J. Fluid Mech. 522, 303–327.CrossRefGoogle Scholar
Winter, K.G. 1979 An outline of the techniques available for the measurement of skin friction in turbulent boundary layers. Prog. Aerosp. Sci. 18, 1–57.CrossRefGoogle Scholar
Woodcock, J.D. & Marusic, I. 2015 The statistical behaviour of attached eddies. Phys. Fluids 27 (1), 015104.CrossRefGoogle Scholar
Yang, X.I.A., Baidya, R., Lv, Y. & Marusic, I. 2018 A hierarchical random additive model for the spanwise and wall-normal velocities in wall-bounded flows at high Reynolds numbers. Phys. Rev. Fluids 3 (12), 124606.CrossRefGoogle Scholar
Zimmerman, S., Morrill-Winter, C. & Klewicki, J. 2017 Design and implementation of a hot-wire probe for simultaneous velocity and vorticity vector measurements in boundary layers. Exp. Fluids 58 (10), 148.CrossRefGoogle Scholar
Zimmerman, S., et al. . 2019 A comparative study of the velocity and vorticity structure in pipes and boundary layers at friction Reynolds numbers up to $10^4$. J. Fluid Mech. 869, 182–213.CrossRefGoogle Scholar