Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gómez-de-Segura, G.
Sharma, A.
and
García-Mayoral, R.
2018.
Turbulent Drag Reduction Using Anisotropic Permeable Substrates.
Flow, Turbulence and Combustion,
Vol. 100,
Issue. 4,
p.
995.
Suga, Kazuhiko
Okazaki, Yuki
Ho, Unde
and
Kuwata, Yusuke
2018.
Anisotropic wall permeability effects on turbulent channel flows.
Journal of Fluid Mechanics,
Vol. 855,
Issue. ,
p.
983.
Yang, Guang
Weigand, Bernhard
Terzis, Alexandros
Weishaupt, Kilian
and
Helmig, Rainer
2018.
Numerical Simulation of Turbulent Flow and Heat Transfer in a Three-Dimensional Channel Coupled with Flow Through Porous Structures.
Transport in Porous Media,
Vol. 122,
Issue. 1,
p.
145.
Valentinova Stoyanova, Petya
Wang, Lei
Sekimoto, Atsushi
Okano, Yasunori
and
Takagi, Youhei
2019.
Effect of Thin and Rough Layers of Porous Materials on Drag.
JOURNAL OF CHEMICAL ENGINEERING OF JAPAN,
Vol. 52,
Issue. 6,
p.
493.
Bottaro, Alessandro
2019.
Flow over natural or engineered surfaces: an adjoint homogenization perspective.
Journal of Fluid Mechanics,
Vol. 877,
Issue. ,
Gómez-de-Segura, G.
and
García-Mayoral, R.
2019.
Turbulent drag reduction by anisotropic permeable substrates – analysis and direct numerical simulations.
Journal of Fluid Mechanics,
Vol. 875,
Issue. ,
p.
124.
García-Mayoral, R
Gómez-de-Segura, G
and
Fairhall, C T
2019.
The control of near-wall turbulence through surface texturing.
Fluid Dynamics Research,
Vol. 51,
Issue. 1,
p.
011410.
Le Clainche, Soledad
Rosti, Marco
and
Brandt, Luca
2020.
Flow structures and shear-stress predictions in the turbulent channel flow over an anisotropic porous wall.
Journal of Physics: Conference Series,
Vol. 1522,
Issue. 1,
p.
012016.
Wang, Fang
Han, Xueli
and
Zhou, Jiakuan
2020.
Dynamics of fluids in layered porous media with anisotropic permeability under a point fluid source.
European Journal of Mechanics - B/Fluids,
Vol. 79,
Issue. ,
p.
324.
Suga, Kazuhiko
Okazaki, Yuki
and
Kuwata, Yusuke
2020.
Characteristics of turbulent square duct flows over porous media.
Journal of Fluid Mechanics,
Vol. 884,
Issue. ,
Okazaki, Yuki
Shimizu, Ayumi
Kuwata, Yusuke
and
Suga, Kazuhiko
2020.
Turbulence characteristics over k-type rib roughened porous walls.
International Journal of Heat and Fluid Flow,
Vol. 82,
Issue. ,
p.
108541.
Nishiyama, Yudai
Kuwata, Yusuke
and
Suga, Kazuhiko
2020.
Direct numerical simulation of turbulent heat transfer over fully resolved anisotropic porous structures.
International Journal of Heat and Fluid Flow,
Vol. 81,
Issue. ,
p.
108515.
Chu, Xu
Wang, Wenkang
Müller, Johannes
Von Schöning, Hendrik
Liu, Yanchao
and
Weigand, Bernhard
2021.
High Performance Computing in Science and Engineering '20.
p.
373.
Chu, Xu
Müller, Johannes
and
Weigand, Bernhard
2021.
High Performance Computing in Science and Engineering '19.
p.
343.
Kazemifar, Farzan
Blois, Gianluca
Aybar, Marcelo
Perez Calleja, Patricia
Nerenberg, Robert
Sinha, Sumit
Hardy, Richard J.
Best, Jim
Sambrook Smith, Gregory H.
and
Christensen, Kenneth T.
2021.
The Effect of Biofilms on Turbulent Flow Over Permeable Beds.
Water Resources Research,
Vol. 57,
Issue. 2,
McCorquodale, Mark W.
and
Munro, R.J.
2021.
Direct effects of boundary permeability on turbulent flows: observations from an experimental study using zero-mean-shear turbulence.
Journal of Fluid Mechanics,
Vol. 915,
Issue. ,
Okazaki, Yuki
Takase, Yumeto
Kuwata, Yusuke
and
Suga, Kazuhiko
2021.
Progress in Turbulence IX.
Vol. 267,
Issue. ,
p.
51.
OKAZAKI, Yuki
TAKASE, Yumeto
KUWATA, Yusuke
and
SUGA, Kazuhiko
2021.
Describing characteristic parameters of turbulence over two-dimensional porous roughness.
Journal of Thermal Science and Technology,
Vol. 16,
Issue. 2,
p.
JTST0027.
Wang, Wenkang
Yang, Guang
Evrim, Cenk
Terzis, Alexandros
Helmig, Rainer
and
Chu, Xu
2021.
An assessment of turbulence transportation near regular and random permeable interfaces.
Physics of Fluids,
Vol. 33,
Issue. 11,
Chu, Xu
Wang, Wenkang
Yang, Guang
Terzis, Alexandros
Helmig, Rainer
and
Weigand, Bernhard
2021.
Transport of Turbulence Across Permeable Interface in a Turbulent Channel Flow: Interface-Resolved Direct Numerical Simulation.
Transport in Porous Media,
Vol. 136,
Issue. 1,
p.
165.
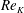 $Re_{K}$), low-speed and high-speed streaks, which are similar to those of solid-wall turbulence, are observed near the walls while at a large
$Re_{K}$), low-speed and high-speed streaks, which are similar to those of solid-wall turbulence, are observed near the walls while at a large 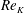 $Re_{K}$ the observed structure is very different from that of the solid-wall turbulence. It is found that the obtained spanwise scales of the structure can be reasonably correlated with the wall normal distance plus the zero-plane displacement which is estimated from the mean velocity profile. With the distribution profiles of the spanwise streak spacing and integral length scales, the transitional change of the turbulence structure over permeable walls is discussed.
$Re_{K}$ the observed structure is very different from that of the solid-wall turbulence. It is found that the obtained spanwise scales of the structure can be reasonably correlated with the wall normal distance plus the zero-plane displacement which is estimated from the mean velocity profile. With the distribution profiles of the spanwise streak spacing and integral length scales, the transitional change of the turbulence structure over permeable walls is discussed.


