Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-29T04:49:11.034Z Has data issue: false hasContentIssue false
  • English
  • Français

Small perturbation evolution in compressible Poiseuille flow: pressure–velocity interactions and obliqueness effects

Published online by Cambridge University Press:  03 February 2017

Zhimin Xie ,
Mona Karimi  and
Sharath S. Girimaji
Zhimin Xie
Affiliation:
Aerospace Engineering Department, Texas A&M University, College Station, TX 77843, USA
Mona Karimi*
Affiliation:
Aerospace Engineering Department, Texas A&M University, College Station, TX 77843, USA Department of Mathematics, Texas A&M University, College Station, TX 77843, USA
Sharath S. Girimaji
Affiliation:
Aerospace Engineering Department, Texas A&M University, College Station, TX 77843, USA Ocean Engineering Department, Texas A&M University, College Station, TX 77843, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Small perturbation evolution in compressible Poiseuille flow is contrasted against the incompressible case using direct simulations and non-modal linear analysis. The onset of compressibility effects leads to a profound change in the behaviour of pressure and its interaction with the velocity field. Linear analysis shows that the most significant compressibility outcome is the harmonic coupling between pressure and wall-normal velocity perturbations. Oscillations in normal perturbations can lead to periods of negative production causing suppression of perturbation growth. The extent of the influence of compressibility can be characterized in terms of an effective gradient Mach number (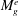$M_{g}^{e}$). Analysis shows that 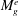$M_{g}^{e}$ diminishes as the angle of the perturbation increases with respect to the shear plane. Direct numerical simulations show that streamwise perturbations, which would lead to Tollmien–Schlichting instability in the incompressible case, are completely suppressed in the compressible case and experience the highest 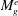$M_{g}^{e}$. At the other extreme, computations reveal that spanwise perturbations, which experience negligible 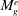$M_{g}^{e}$, are entirely unaltered from the incompressible case. Perturbation behaviour at intermediate obliqueness angles is established. Moreover, the underlying pressure–velocity interactions are explicated.

JFM classification

Compressible Flows: Compressible boundary layers Compressible Flows: Compressible Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 814 , 10 March 2017 , pp. 249 - 276
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baines, P. G., Majumdar, S. J. & Mitsudera, H. 1996 The mechanics of the Tollmien–Schlichting wave. J. Fluid Mech. 312, 107–124.Google Scholar
Bertsch, R. L., Suman, S. & Girimaji, S. S. 2012 Rapid distortion analysis of high Mach number homogeneous shear flows: characterization of flow-thermodynamics interaction regimes. Phys. Fluids 24, 125106.Google Scholar
Butler, K. M. & Farrell, B. F. 1992 Three-dimensional optimal perturbations in viscous shear flow. Phys. Fluids A 4 (8), 1637–1650.CrossRefGoogle Scholar
Davey, A. 1973 A simple numerical method for solving Orr–Sommerfeld problems. Q. J. Mech. Appl. Maths 26, 401–411.Google Scholar
Ellingsen, T. & Palm, E. 1975 Stability of linear flow. Phys. Fluids 18 (4), 487–488.CrossRefGoogle Scholar
Gomez, C. A. & Girimaji, S. S. 2013 Toward second-moment closure modelling of compressible shear flows. J. Fluid Mech. 733, 325–369.Google Scholar
Gomez, C. A. & Girimaji, S. S. 2014 Explicit algebraic Reynolds stress model (earsm) for compressible shear flows. Theor. Comput. Fluid Dyn. 28 (2), 171–196.Google Scholar
Hanifi, A. & Henningson, D. S. 1998 The compressible inviscid algebraic instability for streamwise independent disturbances. Phys. Fluids 10 (8), 1784–1786.Google Scholar
Heiser, W. H. & Pratt, D. T. 1994 Hypersonic Airbreathing Propulsion. AIAA.CrossRefGoogle Scholar
Howarth, L. 1948 Concerning the effect of compressibility on laminar boundary layers and their separation. Proc. R. Soc. Lond. A 194 (1036), 16–42.Google Scholar
Karimi, M. & Girimaji, S. S. 2016 Suppression mechanism of Kelvin–Helmholtz instability in compressible fluid flows. Phys. Rev. E 93, 041102.CrossRefGoogle ScholarPubMed
Kerimo, J. & Girimaji, S. S. 2007 Boltzmann-BGK approach to simulating weakly compressible 3D turbulence: comparison between lattice Boltzmann and gas kinetic methods. J. Turbul. 8 (46), 1–16.Google Scholar
Kumar, G., Bertsch, R. L. & Girimaji, S. S. 2014 Stabilizing action of pressure in homogeneous compressible shear flows: effect of Mach number and perturbation obliqueness. J. Fluid Mech. 760, 540–566.Google Scholar
Kumar, G., Bertsch, R., Venugopal, V. & Girimaji, S. S. 2015 Toward control of compressible shear flows: investigation of possible flow mechanisms. In Advances in Computation, Modeling and Control of Transitional and Turbulent Flows, pp. 397–404. World Scientific.Google Scholar
Kumar, G., Girimaji, S. S. & Kerimo, J. 2013 WENO-enhanced gas-kinetic scheme for direct simulations of compressible transition and turbulence. J. Comput. Phys. 234, 499–523.CrossRefGoogle Scholar
Landahl, M. T. 1980 A note on an algebraic instability of inviscid parallel shear flows. J. Fluid Mech. 98, 243–251.Google Scholar
Lavin, T. A., Girimaji, S. S., Suman, S. & Yu, H. 2012 Flow-thermodynamics interactions in rapidly-sheared compressible turbulence. Theor. Comput. Fluid Dyn. 26 (6), 501–522.CrossRefGoogle Scholar
Lee, K., Venugopal, V. & Girimaji, S. S. 2016 Pressure-strain energy redistribution in compressible turbulence: return-to-isotropy versus kinetic-potential energy equipartition. Phys. Scr. 91, 084006.Google Scholar
Liang, C., Premasuthan, S. & Jameson, A.2009 Large eddy simulation of compressible turbulent channel flow with spectral difference method. AIAA Paper 2009-402.CrossRefGoogle Scholar
Lifschitz, A. & Hameiri, E. 1991 Local stability conditions in fluid dynamics. Phys. Fluids A 3 (11), 2644–2651.CrossRefGoogle Scholar
Livescu, D. & Madnia, C. K. 2004 Small scale structure of homogeneous turbulent shear flow. Phys. Fluids 16 (8), 2864–2876.Google Scholar
Mack, L. M.1984 Boundary-layer linear stability theory. AGARD Report No. 709.Google Scholar
May, G., Srinivasan, B. & Jameson, A. 2007 An improved gas-kinetic BGK finite-volume method for three-dimensional transonic flow. J. Comput. Phys. 220, 856–878.Google Scholar
Reddy, J. N. 1984 Energy and Variational Methods in Applied Mechanics. Wiley.Google Scholar
Sarkar, S. 1995 The stabilizing effect of compressibility in turbulent shear flow. J. Fluid Mech. 282, 163–186.CrossRefGoogle Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows, Applied Mathematical Sciences, vol. 142. Springer.Google Scholar
Simone, A., Coleman, G. N. & Cambon, C. 1997 The effect of compressibility on turbulent shear flow: a rapid-distortion-theory and direct-numerical-simulation study. J. Fluid Mech. 330, 307–338.Google Scholar
Sivasubramanian, J. & Fasel, H. F. 2014 Numerical investigation of the development of three-dimensional wavepackets in a sharp cone boundary layer at Mach 6. J. Fluid Mech. 756, 600–649.Google Scholar
Thomson, W. 1887 Stability of fluid motion: rectilinear motion of viscous fluid between two parallel planes. Phil. Mag. 24 (147), 188–196.Google Scholar
Tichenor, N. R., Humble, R. A. & Bowersox, R. D. W. 2013 Response of a hypersonic turbulent boundary layer to favourable pressure gradients. J. Fluid Mech. 722, 187–213.Google Scholar
Xie, Z. & Girimaji, S. S. 2014 Instability of Poiseuille flow at extreme Mach numbers: linear analysis and simulations. Phys. Rev. E. 89, 043001.Google Scholar
Xu, K. 2001 A gas-kinetic BGK scheme for the Navier–Stokes equations and its connection with artificial dissipation and Godunov method. J. Comput. Phys. 171 (1), 289–335.Google Scholar