Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T16:48:36.971Z Has data issue: false hasContentIssue false
  • English
  • Français

Slipping moving contact lines: critical roles of de Gennes’s ‘foot’ in dynamic wetting

Published online by Cambridge University Press:  20 June 2019

Hsien-Hung Wei Open the ORCID record for Hsien-Hung Wei [Opens in a new window] ,
Heng-Kwong Tsao  and
Kang-Ching Chu
Hsien-Hung Wei*
Affiliation:
Department of Chemical Engineering, National Cheng Kung University, Tainan 701, Taiwan
Heng-Kwong Tsao
Affiliation:
Department of Chemical and Materials Engineering, National Central University, Jhongli 320, Taiwan
Kang-Ching Chu
Affiliation:
Department of Chemical and Materials Engineering, National Central University, Jhongli 320, Taiwan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In the context of dynamic wetting, wall slip is often treated as a microscopic effect for removing viscous stress singularity at a moving contact line. In most drop spreading experiments, however, a considerable amount of slip may occur due to the use of polymer liquids such as silicone oils, which may cause significant deviations from the classical Tanner–de Gennes theory. Here we show that many classical results for complete wetting fluids may no longer hold due to wall slip, depending crucially on the extent of de Gennes’s slipping ‘foot’ to the relevant length scales at both the macroscopic and microscopic levels. At the macroscopic level, we find that for given liquid height 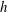$h$ and slip length 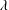$\unicode[STIX]{x1D706}$, the apparent dynamic contact angle 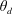$\unicode[STIX]{x1D703}_{d}$ can change from Tanner’s law 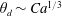$\unicode[STIX]{x1D703}_{d}\sim Ca^{1/3}$ for 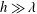$h\gg \unicode[STIX]{x1D706}$ to the strong-slip law $\unicode[STIX]{x1D703}_{d}\sim Ca^{1/2}\,(L/\unicode[STIX]{x1D706})^{1/2}$ for 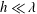$h\ll \unicode[STIX]{x1D706}$, where 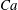$Ca$ is the capillary number and 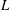$L$ is the macroscopic length scale. Such a no-slip-to-slip transition occurs at the critical capillary number 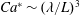$Ca^{\ast }\sim (\unicode[STIX]{x1D706}/L)^{3}$, accompanied by the switch of the ‘foot’ of size 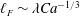$\ell _{F}\sim \unicode[STIX]{x1D706}Ca^{-1/3}$ from the inner scale to the outer scale with respect to 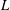$L$. A more generalized dynamic contact angle relationship is also derived, capable of unifying Tanner’s law and the strong-slip law under 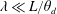$\unicode[STIX]{x1D706}\ll L/\unicode[STIX]{x1D703}_{d}$. We not only confirm the two distinct wetting laws using many-body dissipative particle dynamics simulations, but also provide a rational account for anomalous departures from Tanner’s law seen in experiments (Chen, J. Colloid Interface Sci., vol. 122, 1988, pp. 60–72; Albrecht et al., Phys. Rev. Lett., vol. 68, 1992, pp. 3192–3195). We also show that even for a common spreading drop with small macroscopic slip, slip effects can still be microscopically strong enough to change the microstructure of the contact line. The structure is identified to consist of a strongly slipping precursor film of length 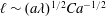$\ell \sim (a\unicode[STIX]{x1D706})^{1/2}Ca^{-1/2}$ followed by a mesoscopic ‘foot’ of width 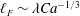$\ell _{F}\sim \unicode[STIX]{x1D706}Ca^{-1/3}$ ahead of the macroscopic wedge, where $a$ is the molecular length. It thus turns out that it is the ‘foot’, rather than the film, contributing to the microscopic length in Tanner’s law, in accordance with the experimental data reported by Kavehpour et al. (Phys. Rev. Lett., vol. 91, 2003, 196104) and Ueno et al. (Trans. ASME J. Heat Transfer, vol. 134, 2012, 051008). The advancement of the microscopic contact line is still led by the film whose length can grow as the 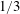$1/3$ power of time due to 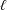$\ell$, as supported by the experiments of Ueno et al. and Mate (Langmuir, vol. 28, 2012, pp. 16821–16827). The present work demonstrates that the behaviour of a moving contact line can be strongly influenced by wall slip. Such slip-mediated dynamic wetting might also provide an alternative means for probing slippery surfaces.

JFM classification

Interfacial Flows (free surface): Capillary flows Interfacial Flows (free surface): Contact lines
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 873 , 25 August 2019 , pp. 110 - 150
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Albrecht, U., Otto, A. & Leiderer, P. 1992 Two-dimensional liquid polymer diffusion: experiment and simulation. Phys. Rev. Lett. 68, 3192–3195.Google Scholar
Anderson, D. M. & Davis, S. H. 1995 The spreading of volatile liquid droplets on heated surfaces. Phys. Fluids 7, 248–265.Google Scholar
Ausserré, D., Picard, A. M. & Léger, L. 1986 Existence and role of the precursor film in the spreading of polymer liquids. Phys. Rev. Lett. 57, 2671–2674.Google Scholar
Barry, A. J. 1946 Viscometric investigation of dimethylsiloxane polymers. J. Appl. Phys. 17, 1020–1024.Google Scholar
Beaglehole, D. 1989 Profiles of the precursor of spreading drops of siloxane oil on glass, fused silica, and mica. J. Phys. Chem. 93, 893–899.Google Scholar
Benintendi, S. W. & Smith, M. K. 1999 The spreading of a non-isothermal liquid droplet. Phys. Fluids 11, 982–989.Google Scholar
Bonn, D., Eggers, J., Indekeu, J., Meunier, J. & Rolley, E. 2009 Wetting and spreading. Rev. Mod. Phys. 81, 739–805.Google Scholar
Brochard, F. & de Gennes, P. G. 1984 Spreading laws for liquid polymer droplets: interpretation of the ‘foot’. J. Phys. Lett. 45, 597–602.Google Scholar
Brochard-Wyart, F., de Gennes, P. G., Hervert, H. & Redon, C. 1994 Wetting and slippage of polymer melts on semi-ideal surfaces. Langmuir 10, 1566–1572.Google Scholar
Chan, K. Y. & Borhan, A. 2006 Spontaneous spreading of surfactant-bearing drops in the sorption-controlled limit. J. Colloid Interface Sci. 302, 374–377.Google Scholar
Chan, T. K., McGraw, J. D., Salez, T., Seemann, R. & Brinkmann, M. 2017 Morphological evolution of microscopic dewetting droplets with slip. J. Fluid Mech. 828, 271–288.Google Scholar
Chen, J.-D. 1988 Experiments on a spreading drop and its contact angle on a solid. J. Colloid Interface Sci. 122, 60–72.Google Scholar
Colinet, P. & Rednikov, A. 2011 On integrable singularities and apparent contact angles within a classical paradigm. Eur. Phys. J. Spec. Top. 197, 89–113.Google Scholar
Cox, R. G. 1986 The dynamics of the spreading of liquids on a solid surface. Part 1. Viscous flow. J. Fluid Mech. 168, 169–194.Google Scholar
Duffy, B. R. & Wilson, S. K. 1997 A third-order differential equation arising in thin-film flows and relevant to Tanner’s law. Appl. Math. Lett. 10, 63–68.Google Scholar
Eggers, J. & Stone, H. A. 2004 Characteristic lengths at moving contact lines for a perfectly wetting fluid: the influence of speed on the dynamic contact angle. J. Fluid Mech. 505, 309–321.Google Scholar
Eggers, J. 2004 Toward a description of contact line motion at higher capillary numbers. Phys. Fluids 16, 3491–3494.Google Scholar
Eggers, J. 2005a Contact line motion for partially wetting fluids. Phys. Rev. E 72, 061605.Google Scholar
Eggers, J. 2005b Existence of receding and advancing contact line. Phys. Fluids 17, 082106.Google Scholar
Eggers, J. & Fontelos, M. A. 2015 Singularities: Formation, Structure, and Propagation. Cambridge University Press.Google Scholar
de Gennes, P. G. 1979 Écoulements viscométriques de polymères enchevêtrés. C. R. Acad. Sci. Paris Sér. B 288, 219–220.Google Scholar
de Gennes, P. G. 1985 Wetting: statics and dynamics. Rev. Mod. Phys. 57, 827–863.Google Scholar
de Gennes, P. G. 1986 Deposition of Langmuir–Blodgett layers. Colloid Polym. Sci. 264, 463–465.Google Scholar
Haley, P. J. & Miksis, M. J. 1991 The effect of the contact line on droplet spreading. J. Fluid Mech. 223, 57–81.Google Scholar
Halpern, D., Li, Y.-C. & Wei, H.-H. 2015 Slip-induced suppression of Marangoni film thickening in surfactant-retarded Landau–Levich–Bretherton flows. J. Fluid Mech. 781, 578–594.Google Scholar
Halpern, D. & Wei, H.-H. 2017 Slip-enhanced drop formation in liquid falling down a vertical fibre. J. Fluid Mech. 820, 42–60.Google Scholar
Hervet, H. & de Gennes, P. G. 1984 Dynamique du mouillage: films précurseurs sur solid ‘sec’. C. R. Acad. Sci. Paris II 299, 499–503.Google Scholar
Hocking, L. M. 1977 A moving fluid interface. Part 2. The removal of the force singularity by a slip flow. J. Fluid Mech. 79, 209–229.Google Scholar
Hocking, L. M. 1983 The spreading of a thin drop by gravity and capillarity. Q. J. Mech. Appl. Maths 36, 55–69.Google Scholar
Hocking, L. M. 1992 Rival contact-angle models and the spreading of drops. J. Fluid Mech. 239, 671–681.Google Scholar
Hocking, L. M. & Rivers, A. D. 1982 The spreading of a drop by capillary action. J. Fluid Mech. 121, 425–442.Google Scholar
Hoffman, R. L. 1975 A study of the advancing interface. I. Interface shape in liquid-gas systems. J. Colloid Interface Sci. 50, 228–241.Google Scholar
Huh, C. & Mason, S. G. 1977 The steady movement of a liquid meniscus in a capillary tube. J. Fluid Mech. 81, 401–419.Google Scholar
Huh, C. & Scriven, L. E. 1971 Hydrodynamic model of steady movement of a solid/liquid/fluid contact line. J. Colloid Interface Sci. 35, 85–101.Google Scholar
Kalliadasis, S. & Chang, H.-C. 1996 Dynamics of liquid spreading on solid surfaces. Ind. Engng Chem. Res. 35, 2860–2874.Google Scholar
Karapetsas, G., Sahu, K. C. & Matar, O. K. 2013 Effect of contact line dynamics on the thermocapillary motion of a droplet on an inclined plate. Langmuir 29, 8892–8906.Google Scholar
Kavehpour, H. P., Ovryn, B. & McKinley, G. H. 2003 Microscopic and macroscopic structure of the precursor layer in spreading viscous drops. Phys. Rev. Lett. 91, 196104.Google Scholar
Lacey, A.-A. 1982 The motion with slip of a thin viscous droplet over a solid surface. Stud. Appl. Maths 67, 217–230.Google Scholar
Léger, L., Erman, M., Guinet-Picard, A. M., Ausserré, D. & Strazielle, C. 1998 Precursor film profiles of spreading liquid drops. Phys. Rev. Lett. 60, 2390–2393.Google Scholar
Levinson, P., Cazabat, A. M., Cohen-Stuart, M. A., Heslot, F. & Nicolet, S. 1988 The spreading of macroscopic droplets. Revue Phys. Appl. 23, 1009–1016.Google Scholar
Li, Y.-C., Liao, Y.-C., Wen, T. C. & Wei, H.-H. 2014 Breakdown of the Bretherton law due to wall slippage. J. Fluid Mech. 741, 200–227.Google Scholar
Liao, Y.-C., Li, Y.-C., Chang, Y.-C., Huang, C.-Y. & Wei, H.-H. 2014 Speeding up thermocapillary migration of a confined bubble by wall slip. J. Fluid Mech. 746, 31–52.Google Scholar
Liao, Y.-C., Li, Y.-C. & Wei, H.-H. 2013 Drastic changes in interfacial hydrodynamics due to wall slippage: slip-intensified film thinning, drop spreading, and capillary instability. Phys. Rev. Lett. 111, 136001.Google Scholar
Marsh, J. A., Garoff, S. & Dussan V., E. B. 1993 Dynamic contact angles and hydrodynamics near a moving contact line. Phys. Rev. Lett. 70, 2778–2781.Google Scholar
Mate, C. M. 2012 Anomalous diffusion kinetics of the precursor film that spreads from polymer droplets. Langmuir 28, 16821–16827.Google Scholar
McHale, G., Shirtcliffe, N. J., Aqil, S., Perry, C. C. & Newton, M. I. 2004 Topography driven spreading. Phys. Rev. Lett. 93, 036102.Google Scholar
Münch, A., Wagner, B. & Witelski, T. P. 2005 Lubrication models with small to large slip lengths. J. Engng Maths 53, 359–383.Google Scholar
Navier, C. L. 1823 (appeared in 1827) Memoire sur les lois du mouvement des fluides. Mem. Acad. R. Sci. France 6, 389–440.Google Scholar
Noble, B. A., Mate, C. M. & Raeymaekers, B. 2017 Spreading kinetics of ultrathin liquid films using molecular dynamics. Langmuir 33, 3476–3483.Google Scholar
Pahlavan, A. A., Cueto-Felgueroso, L., McKinley, G. H. & Juanes, R. 2015 Thin films in partial wetting: internal selection of contact-line dynamics. Phys. Rev. Lett. 115, 034502.Google Scholar
Savva, N. & Kalliadasis, S. 2009 Two-dimensional droplet spreading over topographical substrates. Phys. Fluids 21, 092102.Google Scholar
Savva, N. & Kalliadasis, S. 2011 Dynamics of moving contact lines: a comparison between slip and precursor film models. Europhys. Lett. 94, 64004.Google Scholar
Sibley, D. N., Nold, A. & Kalliadasis, S. 2015 The asymptotics of the moving contact line: cracking an old nut. J. Fluid Mech. 764, 445–462.Google Scholar
Snoeijer, J. H. 2006 Free-surface flows with large slopes: beyond lubrication theory. Phys. Fluids 18, 021701.Google Scholar
Snoeijer, J. H. & Andreotti, B. 2013 Moving contact lines: scales, regimes, and dynamical transitions. Annu. Rev. Fluid Mech. 45, 269–292.Google Scholar
Ström, G., Fredriksson, M., Stenius, P. & Radoev, B. 1990 Kinetics of steady-state wetting. J. Colloid Interface Sci. 134, 107–116.Google Scholar
Tanner, L. H. 1979 The spreading of silicone oil drops on horizontal surfaces. J. Phys. D 12, 1473–1484.Google Scholar
Ueno, I., Hirose, K., Kizaki, Y., Kisara, Y. & Fukuhara, Y. 2012 Precursor film formation process ahead macroscopic contact line of spreading droplet on smooth substrate. Trans. ASME J. Heat Transfer 134, 051008.Google Scholar
Voinov, O. V. 1976 Hydrodynamics of wetting. Fluid Dyn. 11, 714–721.Google Scholar
Wei, H.-H. 2018 Marangoni-enhanced capillary wetting in surfactant-driven superspreading. J. Fluid Mech. 855, 181–209.Google Scholar
Weng, Y.-H., Wu, C.-J., Tsao, H.-K. & Sheng, Y.-J. 2017 Spreading dynamics of a precursor film of nanodrops on total wetting surfaces. Phys. Chem. Chem. Phys. 19, 27786–27794.Google Scholar
Zhou, M.-Y. & Sheng, P. 1990 Dynamics of immiscible-fluid displacement in a capillary tube. Phys. Rev. Lett. 64, 882–885.Google Scholar