Article contents
Slipping free jet flow near channel exit at moderate Reynolds number for large slip length
Published online by Cambridge University Press: 22 March 2016
Abstract
The flow of a slipping fluid jet is examined theoretically as it emerges from a channel at moderate Reynolds number. The ratio of the slip length to the channel width 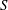 $S$ is assumed to be of order one, one order of magnitude larger than the perturbation parameter
$S$ is assumed to be of order one, one order of magnitude larger than the perturbation parameter 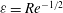 ${\it\varepsilon}=Re^{-1/2}$,
${\it\varepsilon}=Re^{-1/2}$, 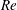 $Re$ being the Reynolds number. Poiseuille flow conditions are assumed to prevail far upstream from the exit. The problem is solved using the method of matched asymptotic expansions. A similarity solution is obtained in the inner layer of the free surface, with the outer layer extending to the jet centreline. The inner-layer thickness grows like
$Re$ being the Reynolds number. Poiseuille flow conditions are assumed to prevail far upstream from the exit. The problem is solved using the method of matched asymptotic expansions. A similarity solution is obtained in the inner layer of the free surface, with the outer layer extending to the jet centreline. The inner-layer thickness grows like 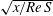 $\sqrt{x/Re\,S}$. A slipping jet is found to contract like
$\sqrt{x/Re\,S}$. A slipping jet is found to contract like 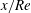 $x/Re$ very near and far from the channel exit, but does not have a definite behaviour in between compared to
$x/Re$ very near and far from the channel exit, but does not have a definite behaviour in between compared to 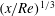 $(x/Re)^{1/3}$ for an adhering jet,
$(x/Re)^{1/3}$ for an adhering jet,  $x$ being the distance from the channel exit. Eventually, the jet reaches uniform conditions far downstream. As in the case of entry flow, there is a rapid departure in flow behaviour for a slipping jet from the
$x$ being the distance from the channel exit. Eventually, the jet reaches uniform conditions far downstream. As in the case of entry flow, there is a rapid departure in flow behaviour for a slipping jet from the 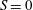 $S=0$ limit. This rapid change is notably observed in the drop of boundary-layer thickness, increase in exit and relaxation lengths as well as in jet width with slip length. Finally, the connections with microchannel and hydrophobic flows are highlighted.
$S=0$ limit. This rapid change is notably observed in the drop of boundary-layer thickness, increase in exit and relaxation lengths as well as in jet width with slip length. Finally, the connections with microchannel and hydrophobic flows are highlighted.
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 7
- Cited by



