Article contents
Slip-enhanced Rayleigh–Plateau instability of a liquid film on a fibre
Published online by Cambridge University Press: 09 January 2023
Abstract
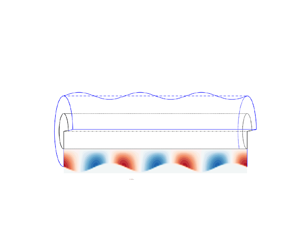
Boundary conditions at a liquid–solid interface are crucial to dynamics of a liquid film coated on a fibre. Here, a theoretical framework based on axisymmetric Stokes equations is developed to explore the influence of liquid–solid slip on the Rayleigh–Plateau instability of a cylindrical film on a fibre. The new model not only shows that the slip-enhanced growth rate of perturbations is overestimated by the classical lubrication model, but also indicates a slip-dependent dominant wavelength, instead of a constant value obtained by the lubrication method, which leads to larger drops formed on a more slippery fibre. The theoretical findings are validated by direct numerical simulations of Navier–Stokes equations via a volume-of-fluid method. Additionally, the slip-dependent dominant wavelengths predicted by our model agree with the experimental results provided by Haefner et al. (Nat. Commun., vol. 6, issue 1, 2015, 7409).
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
REFERENCES
- 7
- Cited by



