Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-12-01T04:00:04.508Z Has data issue: false hasContentIssue false
  • English
  • Français

Slip-enhanced drop formation in a liquid falling down a vertical fibre

Published online by Cambridge University Press:  02 May 2017

David Halpern Open the ORCID record for David Halpern [Opens in a new window]  and
Hsien-Hung Wei
David Halpern
Affiliation:
Department of Mathematics, University of Alabama, Tuscaloosa AL 35487, USA
Hsien-Hung Wei*
Affiliation:
Department of Chemical Engineering, National Cheng Kung University, Tainan 701, Taiwan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a liquid film falling down along a vertical fibre, classical theory (Kalliadasis & Chang J. Fluid Mech., vol. 261, 1994, pp. 135–168; Yu & Hinch J. Fluid Mech., vol. 737, 2013, pp. 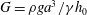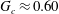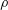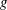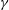232–248) showed that drop formation can occur due to capillary instability when the Bond number $G=\unicode[STIX]{x1D70C}ga^{3}/\unicode[STIX]{x1D6FE}h_{0}$ is below the critical value $G_{c}\approx 0.60$, where $\unicode[STIX]{x1D70C}$ is the fluid density, $g$ is the gravitational acceleration, $a$ is the fibre radius, $\unicode[STIX]{x1D6FE}$ is the surface tension and 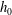$h_{0}$ is the unperturbed film thickness. However, the experiment by Quéré (Europhys. Lett., vol. 13 (8), 1990, pp. 721–726) found 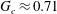$G_{c}\approx 0.71$, which is slightly greater than the above theoretical value. Here we offer a plausible way to resolve this discrepancy by including additional wall slip whose amount can be measured by the slip parameter 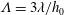$\unicode[STIX]{x1D6EC}=3\unicode[STIX]{x1D706}/h_{0}$, where 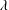$\unicode[STIX]{x1D706}$ is the slip length. Using lubrication theory, we find that wall slip promotes capillary instability and, hence, enhances drop formation. In particular, when slip effects are strong (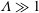$\unicode[STIX]{x1D6EC}\gg 1$), the transition films and the drop height scale as 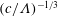$(c/\unicode[STIX]{x1D6EC})^{-1/3}$ and 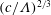$(c/\unicode[STIX]{x1D6EC})^{2/3}$, respectively, distinct from those found by Yu & Hinch for the no-slip case where $c$ is the travelling speed. In addition, for 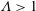$\unicode[STIX]{x1D6EC}>1$, 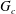$G_{c}$ is found to increase with 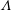$\unicode[STIX]{x1D6EC}$ according to 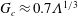$G_{c}\approx 0.7\unicode[STIX]{x1D6EC}^{1/3}$, offering a possible explanation why the $G_{c}$ found by Quéré is slightly greater than that predicted by the no-slip model. Using the above expression, the estimated slip length in Quéré’s experiment is found to be of the order of several micrometres, consistent with the typical slip length range 1–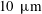$10~\unicode[STIX]{x03BC}\text{m}$ for polymeric liquids such as silicone oil used in his experiment. The existence of wall slip in Quéré’s experiment is further supported by the observation that the film thinning kinetics exhibits the no-slip result 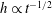$h\propto t^{-1/2}$ for early times and changes to the strong slip result 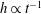$h\propto t^{-1}$, where 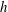$h$ is the film thickness. We also show that when the film is ultrathin, although capillary instability can become further amplified by strong slip effects, the instability can be arrested by the equally intensified gravity draining in the weakly nonlinear regime whose dynamics is governed by the Kuramoto–Sivashinsky equation.

JFM classification

Interfacial Flows (free surface): Capillary flows Low-Reynolds-number flows: Lubrication theory Interfacial Flows (free surface): Thin films
Type
Papers
Information
Journal of Fluid Mechanics , Volume 820 , 10 June 2017 , pp. 42 - 60
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bretherton, F. P. 1961 The motion of long bubbles in tubes. J. Fluid Mech. 10 (2), 166–188.Google Scholar
Brochard-Wyart, F., de Gennes, P.-G., Hervert, H. & Redon, C. 1994 Wetting and slippage of polymer melts on semi-ideal surfaces. Langmuir 10 (5), 1566–1572.Google Scholar
Chang, H. C. & Demekhin, E. A. 1999 Mechanism for drop formation on a coated vertical fibre. J. Fluid Mech. 380, 233–255.Google Scholar
Chen, J.-D. 1988 Experiments on a spreading drop and its contact angle on a solid. J. Colloid Interface Sci. 122 (1), 60–72.CrossRefGoogle Scholar
Craster, R. V. & Matar, O. K. 2006 On viscous beads flowing down a vertical fibre. J. Fluid Mech. 553, 85–105.Google Scholar
Duprat, C., Ruyer-Quil, C., Kalliadasis, S. & Giorgiutti-Dauphine, F. 2007 Absolute and convective instabilities of a viscous film flowing down a vertical fibre. Phys. Rev. Lett. 98 (24), 244502.CrossRefGoogle Scholar
Frenkel, A. L. 1992 Nonlinear theory of strongly undulating thin films flowing down vertical cylinders. Europhys. Lett. 18 (7), 583–588.CrossRefGoogle Scholar
de Gennes, P.-G. 1985 Wetting: statics and dynamics. Rev. Mod. Phys. 57 (3), 827–863.Google Scholar
Haefner, S., Benzaquen, M., Baumchen, O., Salez, T., Peters, R., McGraw, J. D., Jacobs, K., Raphael, E. & Dalnoki-Veress, K. 2015 Influence of slip on the Plateau–Rayleigh instability on a fibre. Nat. Commun. 6, 7409.Google Scholar
Halpern, D., Li, Y.-C. & Wei, H.-H. 2015 Slip-induced suppression of Marangoni film thickening in surfactant-retarded Landau–Levich–Bretherton flows. J. Fluid Mech. 781, 578–594.Google Scholar
Hammond, P. S. 1983 Nonlinear adjustment of a thin annular film of viscous fluid surrounding a thread of another within a circular pipe. J. Fluid Mech. 137, 363–384.CrossRefGoogle Scholar
Kalliadasis, S. & Chang, H.-C. 1994 Drop formation during coating of vertical fibres. J. Fluid Mech. 261, 135–168.Google Scholar
Kalliadasis, S., Ruyer-Quil, C., Scheid, B. & Velarde, M. G. 2011 Falling Liquid Films, vol. 176. Springer Science & Business Media.Google Scholar
Kerchman, V. 1995 Strongly nonlinear interfacial dynamics in core-annular flows. J. Fluid Mech. 290, 131–166.CrossRefGoogle Scholar
Kerchman, V. I. & Frenkel, A. L. 1994 Interactions of coherent structures in a film flow – simulations of a highly nonlinear evolution equation. Theor. Comput. Fluid Dyn. 6 (4), 235–254.Google Scholar
Kliakhandler, I. L., Davis, S. H. & Bankoff, S. G. 2001 Viscous beads on vertical fibre. J. Fluid Mech. 429, 381–390.CrossRefGoogle Scholar
Landau, L. D. & Levich, V. G. 1942 Dragging of a liquid by a moving plate. Acta Physicochim. USSR 17, 42–54.Google Scholar
Lauga, E., Brenner, M. P. & Stone, H. A. 2007 Microfluidics: The No-Slip Boundary Condition, pp. 1219–1240. Springer.Google Scholar
Li, Y. C., Liao, Y. C., Wen, T. C. & Wei, H.-H. 2014 Breakdown of the Bretherton law due to wall slippage. J. Fluid Mech. 741, 200–227.Google Scholar
Liao, Y. C., Li, Y. C., Chang, Y. C., Huang, C. Y. & Wei, H.-H. 2014 Speeding up thermocapillary migration of a confined bubble by wall slip. J. Fluid Mech. 746, 31–52.Google Scholar
Liao, Y. C., Li, Y. C. & Wei, H.-H. 2013 Drastic changes in interfacial hydrodynamics due to wall slippage: slip-intensified film thinning, drop spreading, and capillary instability. Phys. Rev. Lett. 111 (13), 136001.CrossRefGoogle ScholarPubMed
Quéré, D. 1990 Thin-films flowing on vertical fibres. Europhys. Lett. 13 (8), 721–726.CrossRefGoogle Scholar
Ruyer-Quil, C., Treveleyan, P., Giorgiutti-Dauphiné, F., Duprat, C. & Kalliadasis, S. 2008 Modelling film flows down a fibre. J. Fluid Mech. 603, 431–462.CrossRefGoogle Scholar
Yu, L. Y. & Hinch, J. 2013 The velocity of ‘large’ viscous drops falling on a coated vertical fibre. J. Fluid Mech. 737, 232–248.Google Scholar