Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-30T18:54:44.488Z Has data issue: false hasContentIssue false
  • English
  • Français

Slender-body approximations for advection–diffusion problems

Published online by Cambridge University Press:  06 March 2015

Ory Schnitzer
Ory Schnitzer*
Affiliation:
Department of Mathematics, Imperial College London, South Kensington Campus, London SW7 2AZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider steady advection–diffusion about a slender body of revolution at arbitrary 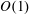$O(1)$ Péclet numbers (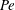$\mathit{Pe}$). The transported scalar attenuates at large distances and is governed by axisymmetric (either Dirichlet or Neumann) data prescribed at the body boundary. The advecting field is assumed to be an axisymmetric Stokes flow approaching a uniform stream at large distances and satisfying impermeability at the boundary; otherwise, the interfacial distribution of tangential velocity is assumed to be arbitrary, irrotational and no-slip Stokes flows being particular cases. Employing the method of matched asymptotic expansions, we develop a systematic scheme for the calculation of the scalar concentration in increasing powers of 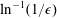$\ln ^{-1}(1/{\it\epsilon})$, 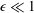${\it\epsilon}\ll 1$ being the body’s characteristic thickness to length ratio. The leading term in the inner expansion coincides with the pure diffusion case, the second term depends nonlinearly on the magnitude of the far-field stream and higher-order terms depend on the boundary distribution of tangential velocity. In the special case of irrotational flow and Neumann boundary conditions the logarithmic expansion terminates, leaving an algebraic error in ${\it\epsilon}$. The general formulae developed can be directly applied to numerous physical scenarios. We here consider the classical problem of forced heat convection from an isothermal body, finding a two-term expansion for 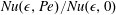$\mathit{Nu}({\it\epsilon},\mathit{Pe})/\mathit{Nu}({\it\epsilon},0)$, the ratio of the Nusselt number to its value at 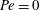$\mathit{Pe}=0$. This ratio is insensitive to the particle shape at the asymptotic orders considered; at moderately large 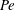$\mathit{Pe}$ (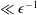$\ll {\it\epsilon}^{-1}$) its deviation from unity is 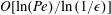$O[\ln (\mathit{Pe})/\text{ln}\,(1/{\it\epsilon})]$, marking the poor effectiveness of advection about slender bodies. The expansion is compared with a numerical computation in the case of a prolate spheroid in both irrotational and no-slip Stokes flows.

JFM classification

Complex Fluids: Colloids Low-Reynolds-number flows: Low-Reynolds-number flows Low-Reynolds-number flows: Slender-body theory
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 768 , 10 April 2015 , R5
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acrivos, A. & Taylor, T. D. 1962 Heat and mass transfer from single spheres in Stokes flow. Phys. Fluids 5 (4), 387–394.CrossRefGoogle Scholar
Anderson, J. L. 1989 Colloid transport by interfacial forces. Annu. Rev. Fluid Mech. 30, 139–165.CrossRefGoogle Scholar
Batchelor, G. K. 1970 Slender-body theory for particles of arbitrary cross-section in Stokes flow. J. Fluid Mech. 44, 419–441.CrossRefGoogle Scholar
Bazant, M. Z. 2004 Conformal mapping of some non-harmonic functions in transport theory. Proc. R. Soc. Lond. A 460 (2045), 1433–1452.CrossRefGoogle Scholar
Brady, J. F. 2011 Particle motion driven by solute gradients with application to autonomous motion: continuum and colloidal perspectives. J. Fluid Mech. 667, 216–259.CrossRefGoogle Scholar
Brenner, H. 1963 Forced convection heat and mass transfer at small Péclet numbers from a particle of arbitrary shape. Chem. Engng Sci. 18 (2), 109–122.CrossRefGoogle Scholar
Choi, J., Margetis, D., Squires, T. M. & Bazant, M. Z. 2005 Steady advection–diffusion around finite absorbers in two-dimensional potential flows. J. Fluid Mech. 536, 155–184.CrossRefGoogle Scholar
Cox, R. G. 1970 The motion of long slender bodies in a viscous fluid. Part 1. General theory. J. Fluid Mech. 44, 791–810.CrossRefGoogle Scholar
Elrick, D. E. 1962 Source functions for diffusion in uniform shear flow. Austral. J. Phys. 15 (3), 283–288.CrossRefGoogle Scholar
Geer, J. 1978 The scattering of a scalar wave by a slender body of revolution. SIAM J. Appl. Maths 34 (2), 348–370.CrossRefGoogle Scholar
Geer, J. 1980 Electromagnetic scattering by a slender body of revolution: axially incident plane wave. SIAM J. Appl. Maths 38 (1), 93–102.CrossRefGoogle Scholar
Goldstein, S. 1929 The steady flow of viscous fluid past a fixed spherical obstacle at small Reynolds numbers. Proc. R. Soc. Lond. A 123 (791), 225–235.Google Scholar
Handelsman, R. A. & Keller, J. B. 1967 Axially symmetric potential flow around a slender body. J. Fluid Mech. 28 (01), 131–147.CrossRefGoogle Scholar
Hinch, E. J. 1991 Perturbation Methods. Cambridge University Press.CrossRefGoogle Scholar
Homentcovschi, D. 1981 Axially symmetric Oseen flow past a slender body of revolution. SIAM J. Appl. Maths 40 (1), 99–112.CrossRefGoogle Scholar
Leal, L. G. 2007 Advanced Transport Phenomena: Fluid Mechanics and Convective Transport Processes. Cambridge University Press.CrossRefGoogle Scholar
Magar, V., Goto, T. & Pedley, T. J. 2003 Nutrient uptake by a self-propelled steady squirmer. Q. J. Mech. Appl. Maths 56 (1), 65–91.CrossRefGoogle Scholar
Michelin, S. & Lauga, E. 2014 Phoretic self-propulsion at finite Péclet numbers. J. Fluid Mech. 747, 572–604.CrossRefGoogle Scholar
Romero, L. A. 1995 Forced convection past a slender body in a saturated porous medium. SIAM J. Appl. Maths 55 (4), 975–985.CrossRefGoogle Scholar
Van Dyke, M. 1964 Perturbation Methods in Fluid Mechanics. Academic.Google Scholar