Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-12-01T08:44:23.936Z Has data issue: false hasContentIssue false
  • English
  • Français

A singular vorticity wave packet within a rapidly rotating vortex: spiralling versus oscillating motions

Published online by Cambridge University Press:  27 June 2019

Philippe Caillol Open the ORCID record for Philippe Caillol [Opens in a new window]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper considers a free vorticity wave packet propagating within a rapidly rotating vortex in the quasi-steady regime, a long time after the wave packet strongly and unsteadily interacted with the vortex. We study a singular, nonlinear, helical and asymmetric shear mode inside a linearly stable, columnar and axisymmetric vortex on the 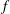$f$-plane. The amplitude-modulated mode enters resonance with the vortex at a certain radius 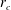$r_{c}$, where the phase angular speed is equal to the rotation frequency. The singularity in the modal equation at 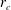$r_{c}$ strongly modifies the flow in the three-dimensional helical critical layer, the region around 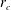$r_{c}$ where the wave/vortex interaction occurs. This interaction generates a vertically sheared three-dimensional mean flow of higher amplitude than the wave packet. The chosen envelope regime assumes the formation of a mean radial velocity of the same order as the wave packet amplitude, leading to the streamlines exhibiting a spiral motion in the neighbourhood of the critical layer. Radar images frequently show such spiral bands in tropical cyclones or tornadoes. Through matched asymptotic expansions, we find an analytical solution of the leading-order equations inside the critical layer. The generalized Batchelor integral condition applied to the quasi-steady, three-dimensional motion inside the separatrices yields a leading-order, non-uniform three-dimensional vorticity. The critical-layer pattern, strongly deformed by the mean radial velocity, loses its symmetries with respect to the azimuthal and radial directions, which makes the leading-order mean radial wave fluxes non-zero. Finally, a stronger wave/vortex interaction occurs with respect to previous studies where a steady neutral vortical mode or an envelope of larger extent was involved.

JFM classification

Waves/Free-surface Flows: Critical layers Geophysical and Geological Flows: Waves in rotating fluids
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 873 , 25 August 2019 , pp. 688 - 741
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. 1956 On steady laminar flow with closed streamlines at large Reynolds number. J. Fluid Mech. 1, 177–190.Google Scholar
Benney, D. J. & Bergeron, R. F. 1969 A new class of nonlinear waves in parallel flows. Stud. Appl. Maths 48, 181–204.Google Scholar
Benney, D. J. & Maslowe, S. A. 1975 The evolution in space and time of nonlinear waves in parallel shear flows. Stud. Appl. Maths 54 (3), 181–205.Google Scholar
Caillol, P. 2012 Multiple vortices induced by a tridimensional critical layer within a rapidly rotating vortex. IMA J. Appl. Maths 77 (3), 282–292.Google Scholar
Caillol, P. 2014 A steady nonlinear and singular vortex Rossby wave within a rapidly rotating vortex. Part I. Theory. Geophys. Astrophys. Fluid Dyn. 108 (4), 387–436.Google Scholar
Caillol, P. 2015 A steady nonlinear and singular vortex Rossby wave within a rapidly rotating vortex. Part II. Application to geophysical vortices. Geophys. Astrophys. Fluid Dyn. 109 (2), 111–144.Google Scholar
Caillol, P. 2017 A singular vortex Rossby wave packet within a rapidly rotating vortex. Phys. Fluids 29 (046601), 1–30.Google Scholar
Caillol, P. & Grimshaw, R. H. J. 2004 Steady multi-polar planar vortices with nonlinear critical layers. Geophys. Astrophys. Fluid Dyn. 98, 473–506.Google Scholar
Caillol, P. & Grimshaw, R. H. J. 2007 Rossby solitary waves in the presence of a critical layer. Stud. Appl. Maths 118, 313–364.Google Scholar
Caillol, P. & Grimshaw, R. H. J. 2008 Rossby elevation waves in the presence of a critical layer. Stud. Appl. Maths 120, 35–64.Google Scholar
Caillol, P. & Grimshaw, R. H. J. 2012 Internal solitary waves with a weakly stratified critical layer. Phys. Fluids 24 (5), 056602.Google Scholar
Caillol, P. & Maslowe, S. A. 2007 The small-vorticity nonlinear critical layer for Kelvin modes on a vortex. Stud. Appl. Maths 118, 221–254.Google Scholar
Campbell, L. J. 2004 Wave-mean flow interactions in a forced Rossby wave packet critical layer. Stud. Appl. Maths 112, 39–85.Google Scholar
Chen, Y., Brunet, G. & Yau, M. K. 2003 Spiral bands in a simulated hurricane. Part II. Wave activity diagnostics. J. Atmos. Sci. 60, 1239–1256.Google Scholar
Chen, Y. & Yau, M. K. 2001 Spiral bands in a simulated hurricane. Part I. Vortex Rossby wave verification. J. Atmos. Sci. 58, 2128–2145.Google Scholar
Corbosiero, K. L., Molinari, J. & Aiyyer, A. R. 2006 The structure and evolution of Hurricane Elena (1985). Part II. Convective asymmetries and evidence for vortex Rossby waves. Mon. Weath. Rev. 134, 3073–3091.Google Scholar
Davis, R. E. 1969 On the high Reynolds number flow over a wavy boundary. J. Fluid Mech. 36, 337–346.Google Scholar
Derzho, O. & Grimshaw, R. 2002 Solitary waves with recirculation zones in axisymmetric rotating flows. J. Fluid Mech. 464, 217–250.Google Scholar
Didlake, A. C., Reasor, P. D., Rogers, R. F. & Lee, W. 2018 Dynamics of the transition from spiral rainbands to a secondary eyewall in Hurricane Earl (2010). J. Atmos. Sci. 75, 2909–2929.Google Scholar
Emanuel, K. A. 1985 An air–sea interaction theory for tropical cyclones. Part I. Steady-state maintenance. J. Atmos. Sci. 43, 585–604.Google Scholar
Gao, C. & Zhu, P. 2016 Vortex Rossby wave propagation in baroclinic tropical cyclone-like vortices. Geophys. Res. Lett. 43 (24), 12578–12589.Google Scholar
Guinn, T. A. & Schubert, W. H. 1993 Hurricane spiral bands. J. Atmos. Sci. 50 (20), 3380–3403.Google Scholar
Haberman, R. 1972 Critical layers in parallel flows. Stud. Appl. Maths 51 (2), 139–161.Google Scholar
Houze, R. A. Jr, Chen, S. S., Lee, W., Rogers, R. F., Moore, J. A., Stossmeister, G. J., Bell, M. M., Cetrone, J., Zhao, W. & Brodzik, S. R. 2006 The hurricane rainband and intensity change experiment: observations and modeling of Hurricanes Katrina, Ophelia, and Rita. Bull. Amer. Meteor. Soc. 87, 1503–1521.Google Scholar
Howard, L. & Gupta, A. 1962 On the hydrodynamic and hydromagnetic stability of swirling flows. J. Fluid Mech. 14 (3), 463–476.Google Scholar
Judt, F. & Chen, S. S. 2010 Convectively generated potential vorticity in rainbands and formation of the secondary eyewall in Hurricane Rita of 2005. J. Atmos. Sci. 129, 3581–3599.Google Scholar
Kivshar, Y. S. & Malomed, B. A. 1989 Dynamics of solitons in nearly integrable systems. Rev. Mod. Phys. 61 (4), 763–916.Google Scholar
Leibovich, S. 1970 Weakly non-linear waves in rotating fluids. J. Fluid Mech. 42, 803–822.Google Scholar
Mallier, R. & Maslowe, S. A. 1999 Weakly nonlinear evolution of a wave packet in a zonal mixing layer. Stud. Appl. Maths 102, 69–85.Google Scholar
Maslowe, S. A. 1986 Critical layers in shear flows. Annu. Rev. Fluid Mech. 18, 405–432.Google Scholar
Moller, J. D. & Montgomery, M. T. 1999 Vortex Rossby waves and hurricane intensification in a barotropic model. J. Atmos. Sci. 56, 1674–1687.Google Scholar
Moller, J. D. & Montgomery, M. T. 2000 Tropical cyclone evolution via potential vorticity anomalies in a three-dimensional balance model. J. Atmos. Sci. 57, 3366–3387.Google Scholar
Montgomery, M. T. & Enagonio, J. 1998 Tropical cyclogenesis via convectively forced vortex Rossby waves in a three-dimensional quasigeostrophic model. J. Atmos. Sci. 55, 3176–3206.Google Scholar
Montgomery, M. T. & Kallenbach, R. J. 1997 A theory for vortex Rossby-waves and its application to spiral bands and intensity changes in hurricanes. Q. J. R. Meteorol. Soc. 123, 435–465.Google Scholar
Nolan, D. S. & Farrell, B. F. 1999 The intensification of two-dimensional swirling flows by stochastic asymmetric forcing. J. Atmos. Sci. 56 (23), 3937–3961.Google Scholar
Qiu, X., Tan, Z. M. & Xiao, Q. 2010 The roles of vortex Rossby waves in hurricane secondary eyewall formation. Mon. Weath. Rev. 138, 2092–2109.Google Scholar
Reasor, P. D., Eastin, M. D. & Gamache, J. F. 2009 Rapidly intensifying Hurricane Guillermo (1997). Part I. Low-wavenumber structure and evolution. Mon. Weath. Rev. 137, 603–631.Google Scholar
Reasor, P. D., Montgomery, M. T., Marks, F. D. & Gamache, J. F. 2000 Low-wavenumber structure and evolution of the hurricane inner core observed by airborne dual-Doppler radar. Mon. Weath. Rev. 128 (6), 1653–1680.Google Scholar
Ruan, K., Zha, Y. & Huang, H. 2014 Contribution of vortex Rossby wave to spiral rainband formation in tropical cyclones. J. Hydro. 26 (5), 725–733.Google Scholar
Shagalov, S. V., Reutov, V. P. & Rybushkina, G. V. 2009 The asymptotic theory of the generation of long-wave structures in critical layers of weakly dissipative jet flows. Izvest. Atmos. Ocean Phys. 45, 629–645.Google Scholar
Velasco Fuentes, O. U. 2005 Vortex filamentation: its onset and its role on axisymmetrization and merger. Dyn. Atmos. Oceans 40, 23–42.Google Scholar
Voronovich, V. V., Pelinovsky, D. E. & Shrira, V. I. 1998a On internal wave-shear flow resonance in shallow water. J. Fluid Mech. 354, 209–237.Google Scholar
Voronovich, V. V., Shrira, V. I. & Stepanyants, Y. A. 1998 Two-dimensional models for nonlinear vorticity waves in shear flows. Stud. Appl. Maths 100, 1–32.Google Scholar
Wang, L., Koblinsky, C., Howden, S. & Beckley, B. 1998 Large-scale Rossby wave in the mid-latitude South Pacific from altimetry data. Geophys. Res. Lett. 25 (2), 179–182.Google Scholar
Wang, T., Zhong, Z. & Wang, J. 2018 Vortex Rossby waves in asymmetric basic flow of typhoons. Adv. Atmos. Sci. 35, 531–539.Google Scholar
Wang, Y. 2002a Vortex Rossby waves in a numerically simulated tropical cyclone. Part I. Overall structure, potential vorticity, and kinetic energy budgets. J. Atmos. Sci. 59, 1213–1238.Google Scholar
Wang, Y. 2002b Vortex Rossby waves in a numerically simulated tropical cyclone. Part II. The role in tropical cyclone structure and intensity changes. J. Atmos. Sci. 59, 1239–1262.Google Scholar
Zhang, J. A., Rogers, R. F., Nolan, D. S. & Marks, F. D. Jr 2011 On the characteristic height scales of the hurricane boundary layer. Mon. Weath. Rev. 139, 2523–2535.Google Scholar