Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-21T11:09:16.610Z Has data issue: false hasContentIssue false
  • English
  • Français

Singular jets during the collapse of drop-impact craters

Published online by Cambridge University Press:  13 June 2018

S. T. Thoroddsen Open the ORCID record for S. T. Thoroddsen [Opens in a new window] ,
K. Takehara ,
H. D. Nguyen  and
T. G. Etoh
S. T. Thoroddsen*
Affiliation:
Division of Physical Sciences and Engineering, King Abdullah University of Science and Technology (KAUST), Thuwal 23955-6900, Saudi Arabia
K. Takehara
Affiliation:
Department of Civil and Environmental Engineering, Kindai University, Higashi-Osaka 577-8502, Japan
H. D. Nguyen
Affiliation:
Department of Civil and Environmental Engineering, Kindai University, Higashi-Osaka 577-8502, Japan Hanoi University of Science and Technology, No. 1 Dai Co Viet Street, Hanoi, Vietnam
T. G. Etoh
Affiliation:
Department of Civil and Environmental Engineering, Kindai University, Higashi-Osaka 577-8502, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

When a drop impacts on a deep pool at moderate velocity it forms a hemispheric crater which subsequently rebounds to the original free-surface level, often forming Worthington jets, which rise vertically out of the crater centre. Under certain impact conditions the crater collapse forms a dimple at its bottom, which pinches off a bubble and is also known to be associated with the formation of a very fast thin jet. Herein we use two ultra-high-speed video cameras to observe simultaneously the dimple collapse and the speed of the resulting jet. 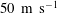The fastest fine jets are observed at speeds of approximately $50~\text{m}~\text{s}^{-1}$ and emerge when the dimple forms a cylinder which retracts without pinching off a bubble. We also identify what appears to be micro-bubbles at the bottom of this cylinder, which we propose are caused by local cavitation from extensional stress in the flow entering the jet. The radial collapse of the dimple does not follow capillary-inertial power laws nor is its bottom driven by a curvature singularity, as has been proposed in some earlier studies. The fastest jets are produced by pure inertial focusing and emerge at finite dimple size, bypassing the pinch-off singularity. These jets emerge from the liquid contained originally in the drop. Finally, we measure directly the compression of the central bubble following the pinch-off and the subsequent large volume oscillation, which occurs at frequencies slightly above the audible range at approximately 23 kHz.

JFM classification

Drops and Bubbles: Bubble dynamics Drops and Bubbles: Drops and Bubbles Acoustics: Hydrodynamic noise
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 848 , 10 August 2018 , R3
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bergmann, R., van der Meer, D., Stijnman, M., Sandtke, M., Prosperetti, A. & Lohse, D. 2006 Giant bubble pinch-off. Phys. Rev. Lett. 96, 154505.CrossRefGoogle ScholarPubMed
Boulton-Stone, J. M. & Blake, J. R. 1993 Gas bubbles bursting at a free surface. J. Fluid Mech. 254, 437–466.CrossRefGoogle Scholar
Brenner, M. P. 2000 Jets from a singular surface. Nature 403, 377–378.CrossRefGoogle ScholarPubMed
Burton, J. C., Waldrep, R. & Taborek, P. 2005 Scaling and instabilities in bubble pinch-off. Phys. Rev. Lett. 94, 184502.CrossRefGoogle ScholarPubMed
Das, S. P. & Hopfinger, E. J. 2008 Parametrically forced gravity waves in a circular cylinder and finite-time singularity. J. Fluid Mech. 599, 205–228.CrossRefGoogle Scholar
Deike, L., Ghabache, E., Liger-Belair, G., Das, A. K., Zaleski, S., Popinet, S. & Séon, T. 2018 Dynamics of jets produced by bursting bubbles. Phys. Rev. Fluids 3, 013603.CrossRefGoogle Scholar
Deng, Q., Anilkumar, V. & Wang, T. G. 2007 The role of viscosity and surface tension in bubble entrapment during drop impact onto a deep liquid pool. J. Fluid Mech. 578, 119–138.CrossRefGoogle Scholar
Duchemin, L., Popinet, S., Josserand, C. & Zaleski, S. 2002 Jet formation in bubbles bursting at a free surface. Phys. Fluids 14, 3000–3008.CrossRefGoogle Scholar
Eggers, J., Fontelos, M. A., Leppinen, D. & Snoeijer, J. 2007 Theory of the collapsing axisymmetric cavity. Phys. Rev. Lett. 98, 094502.CrossRefGoogle ScholarPubMed
Etoh, T. G. et al. 2003 An image sensor which captures 100 consecutive frames at 1000 000 frames s-1 . IEEE Trans. Electron Devices 50, 144–151.CrossRefGoogle Scholar
Ganan-Calvo, A. M. 2017 Revision of bubble bursting: universal scaling laws of top jet drop size and speed. Phys. Rev. Lett. 119, 204502.CrossRefGoogle ScholarPubMed
Gekle, S. & Gordillo, J. M. 2010 Generation and breakup of Worthington jets after cavity collapse. Part 1. Jet formation. J. Fluid Mech. 663, 293–330.CrossRefGoogle Scholar
Gekle, S., Gordillo, J. M., van der Meer, D. & Lohse, D. 2009 High-speed jet formation after solid object impact. Phys. Rev. Lett. 102, 034502.CrossRefGoogle ScholarPubMed
Ghabache, E., Antkowiak, A., Josserand, C. & Séon, T. 2014 On the physics of fizziness: how bubbles bursting controls droplets ejection. Phys. Fluids 26, 121701.CrossRefGoogle Scholar
Gordillo, J. M., Sevilla, A., Rodríguez-Rodríguez, J. & Martínez-Bazán, C. 2005 Axisymmetric bubble pinch-off at high Reynolds numbers. Phys. Rev. Lett. 95, 194501.CrossRefGoogle ScholarPubMed
Inoue, C., Izato, Y., Miyake, A. & Villermaux, E. 2017 Direct self-sustained fragmentation cascade of reactive droplets. Phys. Rev. Lett. 118, 074502.CrossRefGoogle ScholarPubMed
Inoue, C., Koshi, M., Terashima, H., Himeno, T. & Watanabe, T. 2013 Origin of droplets in sparkling fireworks. Sci. Technol. Energetic Mater. 74, 106–111.Google Scholar
Keim, N. C., Moller, P., Zhang, W. W. & Nagel, S. N. 2006 Breakup of air bubbles inwater: memory and breakdown of cylindrical symmetry. Phys. Rev. Lett. 97, 144503.CrossRefGoogle Scholar
Kientzler, C. F., Arons, A. B., Blanchard, D. C. & Woodcock, A. H. 1954 Photographic investigation of the projection of droplets by bubbles bursting at a water surface. Tellus 6, 1–7.CrossRefGoogle Scholar
Krishnan, S., Hopfinger, E. J. & Puthenveettil, B. A. 2017 On the scaling of jetting from bubble collapse at a liquid surface. J. Fluid Mech. 822, 791–812.CrossRefGoogle Scholar
Liow, L. J. 2001 Splash formation by spherical drops. J. Fluid Mech. 427, 73–105.Google Scholar
MacIntyre, F. 1972 Flow patterns in breaking bubbles. J. Geophys. Res. 77, 5211–5228.CrossRefGoogle Scholar
Michon, G.-J., Josserand, C. & Séon, T. 2017 Jet dynamics post drop impact on a deep pool. Phys. Rev. Fluids 2, 023601.CrossRefGoogle Scholar
Morton, D., Rudman, M. & Liow, J.-L. 2000 An investigation of the flow regimes resulting from splashing drops. Phys. Fluids 12, 747–763.CrossRefGoogle Scholar
Oguz, H. N. & Prosperetti, A. 1990 Bubble entrainment by the impact of drops on liquid surfaces. J. Fluid Mech. 219, 143–179.CrossRefGoogle Scholar
Oguz, H. N. & Prosperetti, A. 1991 Numerical calculation of the underwater noise of rain. J. Fluid Mech. 228, 417–442.Google Scholar
Prosperetti, A. & Oguz, H. N. 1993 The impact of drops on liquid surfaces and the underwater noise of rain. Annu. Rev. Fluid Mech. 25, 577–602.CrossRefGoogle Scholar
Pumphrey, H. C. & Elmore, P. A. 1990 The entrainment of bubbles by drop impacts. J. Fluid Mech. 220, 539–567.CrossRefGoogle Scholar
Ray, B., Biswas, G. & Sharma, A. 2015 Regimes during drop impact on a liquid pool. J. Fluid Mech. 768, 492–523.CrossRefGoogle Scholar
Rein, M. 1996 The transition regime between coalescing and splashing drops. J. Fluid Mech. 306, 145–165.CrossRefGoogle Scholar
Séon, T. & Liger-Belair, G. 2017 Effervescence in champagne and sparkling wines: from bubble bursting to droplet evaporation. Eur. Phys. J. Special Top. 226, 117–156.CrossRefGoogle Scholar
Thoraval, M.-J., Takehara, K., Etoh, T. G., Popinet, S., Ray, P., Josserand, C., Zaleski, S. & Thoroddsen, S. T. 2012 Von Kármán vortex street within an impacting drop. Phys. Rev. Lett. 108, 264506.CrossRefGoogle Scholar
Thoroddsen, S. T., Etoh, T. G. & Takehara, K. 2007a Experiments on bubble pinch-off. Phys. Fluids 19, 042101.CrossRefGoogle Scholar
Thoroddsen, S. T., Etoh, T. G. & Takehara, K. 2007b Micro-jetting from wave-focusing on oscillating drops. Phys. Fluids 19, 052101.CrossRefGoogle Scholar
Thoroddsen, S. T., Takehara, K. & Etoh, T. G. 2003 Air entrapment under an impacting drop. J. Fluid Mech. 478, 125–134.CrossRefGoogle Scholar
Tran, T. T., Lee, E. G., Lee, I. S., Woo, N. S., Han, S. M., Kim, Y. J. & Hwang, W. R. 2016 Hydrodynamic extensional stress during the bubble bursting process for bioreactor system design. Korea-Aust. Rheol. J. 28, 315–326.CrossRefGoogle Scholar
Walls, P. L. L., Henaux, L. & Bird, J. C. 2015 Jet drops from bursting bubbles: how gravity and viscosity couple to inhibit droplet production. Phys. Rev. E 92, 021002(R).Google ScholarPubMed
Walls, P. L. L., McRae, O., Natarajan, V., Johnson, C., Antoniou, C. & Bird, J. C. 2017 Quantifying the potential for bursting bubbles to damage suspended cells. Sci. Rep. 7, 15102.CrossRefGoogle ScholarPubMed
Worthington, A. M. & Cole, R. S. 1897 Impact with a liquid surface, studied by the aid of instantaneous photography. Phil. Trans. R. Soc. Lond. A 189, 137–148.Google Scholar
Zeff, B. W., Kleber, B., Fineberg, J. & Lathrop, D. P. 2000 Singularity dynamics in curvature collapse and jet eruption on a fluid surface. Nature 403, 401–404.CrossRefGoogle ScholarPubMed
Zhang, F., Thoraval, M.-J., Thoroddsen, S. T. & Taborek, P. 2015 Partial coalescence from bubbles to drops. J. Fluid Mech. 782, 209–239.CrossRefGoogle Scholar
Zhang, L. V., Toole, J., Fezzaa, K. & Deegan, R. D. 2012 Evolution of the ejecta sheet from the impact of a drop with a deep pool. J. Fluid Mech. 690, 5–15.CrossRefGoogle Scholar

Thoroddsen et al. movie 1

Video with Figure 1(a).

Download Thoroddsen et al. movie 1(Video)
Video 567 KB
Supplementary material: PDF

Thoroddsen et al. supplementary material

Supplementary material

Download Thoroddsen et al. supplementary material(PDF)
PDF 191.5 KB

Thoroddsen et al. movie 2

Video with Figure 1(b).

Download Thoroddsen et al. movie 2(Video)
Video 507.2 KB

Thoroddsen et al. movie 3

Video with Figure 1(c)

Download Thoroddsen et al. movie 3(Video)
Video 331.9 KB

Thoroddsen et al. movie 4

Video with Figure 4(d).

Download Thoroddsen et al. movie 4(Video)
Video 488.2 KB

Thoroddsen et al. movie 5

Video with Figure 7(a).

Download Thoroddsen et al. movie 5(Video)
Video 417.6 KB

Thoroddsen et al. movie 6

Video with Figure 7(b).

Download Thoroddsen et al. movie 6(Video)
Video 485.5 KB

Thoroddsen et al. movie 7

Video with Figure 8.

Download Thoroddsen et al. movie 7(Video)
Video 419.7 KB